Tích giá trị tất cả các nghiệm của phương trình log x 3 2 - 2 log x + 1 = 0 bằng
A. 10 10 9
B. 10
C. 1
D. 10 10
Tất cả các giá trị của tham số m để phương trình log m x = 2 log x + 1 có nghiệm là
![]()
![]()
![]()
![]()
Cho phương trình log2(10x) - 2mlog10xx - log(10x2)=0 . Gọi S là tập chứa tất cả các giá trị nguyên của m thuộc [-10;10] để phương trình đã cho có đúng 3 nghiệm phân biệt . Số phần tử của tập S là
Tìm tất cả các nghiệm của phương trình log x + log ( x - 9 ) = 1
A. {10}
B. {9}
C. {1;9}
D. {-1;10}
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình log ( ( m - 1 ) . 16 x + 2 . 25 x 5 . 20 x ) - 5 x + 1 . 4 x = ( 1 - m ) 4 2 x - 2 . 25 x có hai nghiệm thực phân biệt. Số phần tử của S bằng
![]()
![]()
![]()
![]()
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình log ( ( m - 1 ) . 16 x + 2 . 25 x 5 . 20 x ) - 5 x + 1 . 4 x = ( 1 - m ) 4 2 x - 2 . 25 x có hai nghiệm thực phân biệt. Số phần tử của S bằng
A. 4.
B. 3.
C. 1.
D. 2.
Tổng tất cả các giá trị nghiệm của phương trình log 3 x 2 + x + 3 = 2 là:
A.-6
B.2
C.3
D. -1
Tích giá trị tất cả các nghiệm của phương trình log x 3 2 - 20 log x + 1 = 0 bằng
A. 10 10 9
B. 10
C. 1
D. 10 10
Tích giá trị tất cả các nghiệm của phương trình log 2 x 3 - 20 log x + 1 = 0 bằng
A. 10
B. 10 10 9
C. 1
D. 10 10
Tích giá trị tất cả các nghiệm của phương trình log x 3 2 - 20 log x + 1 = 0 bằng
A. 10 10 9
B. 10
C. 1
D. 10 10
Đáp án A
Phương pháp giải:
Đưa về phương trình bậc hai ẩn logx sử dụng công thức ![]() (giả sử các biểu thức là có nghĩa).
(giả sử các biểu thức là có nghĩa).
Lời giải: ĐK: x > 0
![]()
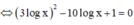
![]()
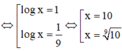
Tích giá trị tất cả các nghiệm của phương trình là: 10 10 9