Tính tổng các giá trị của tham số m để số phức z = m - 1 + 2 m - 1 i 1 - m i là số thực.
A. -3
B. -2
C. -1
D. 0
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thoả mãn z. z =1 và |z-3-4i|=m. Tính tổng các phần tử thuộc S.
A. 10.
B. 42.
C. 52.
D. 40.
Trên tập ℂ , cho số phức z = i + m i - 1 với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z. z ¯ = 5
A. m = -3
B. m = 1
C. m = ± 2
D. m = ± 3
Trên tập ℂ , cho số phức z = i + m i - 1 với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z. z ¯ = 5
A. m = -3
B. m = 1
C. m = ± 2
D. m = ± 3
Trên tập ℂ , cho số phức z = i + m i − 1 , với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z . z ¯ = 5.
A. m = − 3.
B. m = 1.
C. m = ± 2.
D. m = ± 3.
Đáp án D.
Ta có z . z ¯ = 5 ⇔ z 2 = 5 ⇔ m 2 + 1 2 = 5 ⇔ m 2 = 9 ⇔ m = ± 3.
Cho các số phức z 1 = 1, z 2 = 2 − 3 i và các số z thỏa mãn z − 1 − i + z − 3 + i = 2 2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = z − z i + z − z 2 . Tính tổng S = M + m
A. S = 4 + 2 5 .
B. S = 5 + 17 .
C. S = 1 + 10 + 17 .
D. S = 10 + 2 5 .
Đáp án B.
Số phức z 1 = 1 có điểm biểu diễn là A 1 ; 0 , số phức z 2 = 2 − 3 i có điểm biểu diễn là B 2 ; − 3
Gọi E x ; y là điểm biểu diễn của số phức z, khi đó z = x + y i , x , y ∈ ℝ
Suy ra
P = x − 1 + y i + x − 2 + y + 3 i = x − 1 2 + y 2 + x − 2 2 + y + 3 2
⇒ P = E A + E B .
Mặt khác
z − 1 − i + z − 3 + i = 2 2 ⇔ x − 1 + y − 1 i + x − 3 + y + 1 i = 2 2
⇔ x − 1 2 + y − 1 2 + x − 3 2 + y + 1 2 = 2 2 *
Gọi M 1 ; 1 , N 3 ; − 1 thì E M + E N = 2 2 = M N ⇒ Điểm E thuộc đoạn MN.
Ta có phương trình đường thẳng MN là x + y + z − 2 = 0 với x ∈ 1 ; 3
Bài toán trở thành:
Cho điểm E thuộc đoạn MN . Tìm giá trị lớn nhất của biểu thức P = E A + E B
Đặt f ( x ) = x + y − 2. Ta có
f 1 ; 0 = 1 + 0 − 2 = − 1 f 2 ; − 3 = 2 − 3 − 2 = − 3 ⇒ f 1 ; 0 . f 2 ; − 3 = 3 > 0 . Suy ra hai điểm A,B nằm cùng về một phía đối với MN . Gọi A' là điểm đối xứng với A qua MN thì A ' 2 ; 1 .Khi đó
P = E A + E B = E A ' + E B ≥ A ' B = 4 .
Dấu = xảy ra khi và chỉ khi
E ∈ A ' B ⇒ E = A ' B ∩ M N ⇒ E 2 ; 0 hay z = 2.
Do điểm E luôn thuộc đường thẳng MN nên P = E A + E B đạt giá trị lớn nhất khi E ≡ M hoặc E ≡ N .
Có
M A + M B = 1 + 17 N A + N B = 2 5 ⇒ M A + M B > N A + N B ⇒ max P = M A + M B = 1 + 17.
Vậy
M = 1 + 7 , m = 4 ⇒ S = M + m = 5 + 17 .
Cho các số phức z 1 = 1 , z 2 = 2 − 3 i và các số z thỏa mãn z − 1 − i + z − 3 + i = 2 2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = z − z i + z − z 2 . Tính tổng
A. S = 4 + 2 5 .
B. S = 5 + 17 .
C. S = 1 + 10 + 17 .
D. S = 10 + 2 5 .
Tìm tập hợp tất cả các giá trị của tham số m để có đúng 8 số phức z thỏa mãn đồng thời các điều kiện z + z ¯ + z - z ¯ = z 2 và z = m
![]()
![]()
![]()
![]()
Tìm tập hợp tất cả các giá trị của tham số m để có đúng 8 số phức z thỏa mãn đồng thời các điều kiện z + z ¯ + z - z ¯ = z 2 và z = m ?
D. 2 ; 2
B. 2 ; 2 2
C. 2 ; 2
D. 2 ; 2 2
Đặt z=x+yi ta có hệ đều kiện:
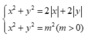
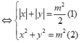
Ta có (1) là tập hợp các cạnh của hình vuông ABCD có tâm là gốc toạ độ độ dài cạnh bằng a = m 2 2 ; là đường tròn (C) có tâm là gốc toạ độ O bán kính bằng R = m.
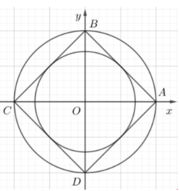
Để có đúng 8 số phức thoả mãn thì (C) phải nằm giữa đường tròn ngoại tiếp và đường tròn nội tiếp hình vuông 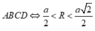
![]()
Chọn đáp án D.
Tìm tập hợp tất cả các giá trị của tham số m để có đúng 4 số phức z thỏa mãn đồng thời các điều kiện z + z ¯ + z - z ¯ = z 2 và z = m ?
A. 2 ; 2 2
B. 2 ; 2 2
C. 2
D. 2 ; 2 2