Nghiệm của hệ phương trình 1 x − 2 y = 1 1 x + 2 y = 2 là:
A. 2 3 ; 4
B. − 2 3 ; 4
C. 2 ; 4
D. − 2 ; − 4
Bài tập 1 Cho hệ phương trình  (1)
(1)
1. Giải hệ phương trình (1) khi m = 3 .
2. Tìm m để hệ phương trình có nghiệm x = ![]() và y =
và y = ![]() .
.
3. Tìm nghiệm của hệ phương trình (1) theo m.
cho phương trình \(x^2-2\left(m-1\right)x+m-3+=0\left(1\right)\)
1.chứng minh phương trình luôn có 2 nghiệm phân biệt
2.tìm một hệ thức liên hệ giữa hai nghiệm của phương trình (1) mà không phụ thuộc vào m
3.tìm giá trị nhỏ nhất của P=x^2+x^2 ( với x1,x2 là nghiệm của phương trình (1)
Cho phương trình (ẩn x):x^2+ 2.(m+2)+4m-1=0(1).chứng minh với mọi giá trị của m phương trình(1) luôn có 2 nghiệm phân biệt .Tìm 1 hệ thức liên hệ giữa 2 nghiệm đó của phương trình (1) không phụ thuộc vào m
1) xét delta là được
2) áp đụng định lý viet ta có x1+x2 = -2(m+2) = -2m-4 => 2x1 + 2x2 = -4m -8
x1.x2 = 4m-1
ta có 2x1 + 2x2 + x1x2 = -4m-8+4m-1 = -9
vậy hệ thức cần lập là 2x1 + 2x2 + x1x2 = -9
delta= (m+2)^2-1(4m-1)=m^2 +5 >0 (luôn đúng với mọi m)
dùng Vi-et: Gọi a và b là hai nghiệm của phương trình
a+b= -2(m+2)
= -4m-4 (1)
ab=4m-1(2)
(1)+(2)
a+b+ab=-5
Cho phương trình ( ẩn x ): x mũ 2 + 2(m+2)x +4m - 1= 0 (1)
a, giải phương trình (1) khi m=2
b, chứng minh rằng với mọi giá trị của m, phương trình (1) luôn có hai nghiệm phân biệt. Tìm một hệ thức liên hệ giữa hai nghiệm của phương trình (1) không phụ thuộc vào m
a, Với m=2 thì phương trình (1) trở thành
x mũ 2 + 2(2+2)x +4.2 -1 =0
<=> x mũ 2 + 8x +7 =0
<=> x mũ 2 + x + 7x +7 =0
<=> (x+1)(x+7) =0
<=> x= -1 hoặc x= -7
b, Ta có:
penta' = (m+2)mũ2 - 4m -1
= m m 2 +4m +4 -4m -1
= m mũ2 +3
vì m mũ2 luôn > hoặc = 0 với mọi m
suy ra m mũ2 +3 luôn >0 với mọi m
suy ra penta' >0 hay có hai nghiệm phân biệt (đpcm)
CÒN PHẦN SAU THÌ MK KO BIẾT LÀM .... THÔNG CẢM
Cho hệ phương trình x + my =2m hoặc mx + y = 1-m (m là tham số )
1.Tìm các giá trị của m để hệ phương trình :
a)Có nghiệm duy nhất. Tìm nghiệm duy nhất đó
b)Vô nghiệm
c)Vô số nghiệm
2.Trong trường hợp hệ phương trình có nghiệm duy nhất (x,y)
a)Hãy tìm giá trị m nguyên để x và y cùng nguyên
b)tìm hệ thức liên hệ giữa x và y không phụ thuộc m
Trong các khẳng định sau, khẳng định nào đúng?
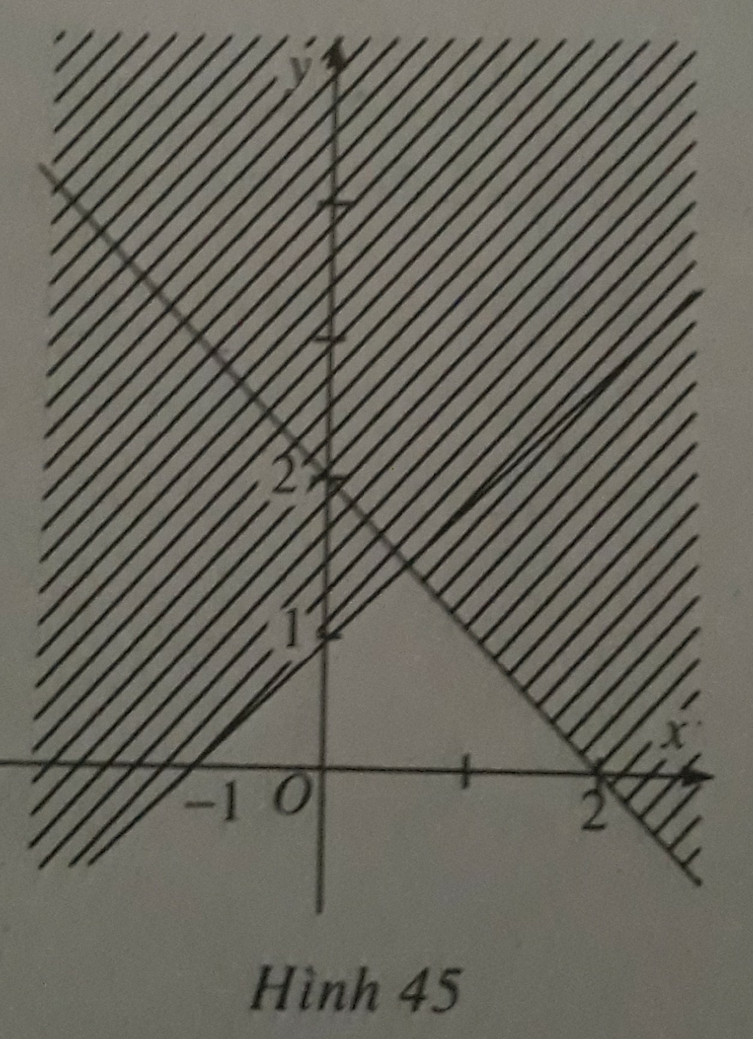
A. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình x + y ≤ 2.
B. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình![]()
và (x; y) = (-1; 1) là một nghiệm của hệ.
C. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình ![]() và (x; y) = (-2; 1) là một nghiệm của hệ.
và (x; y) = (-2; 1) là một nghiệm của hệ.
D. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình 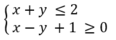 và (x; y) = (1; 0) là một nghiệm của hệ.
và (x; y) = (1; 0) là một nghiệm của hệ.
Cho hệ phương trình:
\(\left\{{}\begin{matrix}2x+my=-5\\x-3y=2\end{matrix}\right.\)
a) Tìm m để hệ phương trình có nghiệm duy nhất, vô nghiệm, vô số nghiệm
b) Với giá trị nào của m thì hệ phương trình có nghiệm duy nhất thỏa mãn x+2y=1
`a,x-3y=2`
`<=>x=3y+2` ta thế vào phương trình trên:
`2(3y+2)+my=-5`
`<=>6y+4+my=-5`
`<=>y(m+6)=-9`
HPT có nghiệm duy nhất:
`<=>m+6 ne 0<=>m ne -6`
HPT vô số nghiệm
`<=>m+6=0,-6=0` vô lý `=>x in {cancel0}`
HPT vô nghiệm
`<=>m+6=0,-6 ne 0<=>m ne -6`
b,HPT có nghiệm duy nhất
`<=>m ne -6`(câu a)
`=>y=-9/(m+6)`
`<=>x=3y+2`
`<=>x=(-27+2m+12)/(m+6)`
`<=>x=(-15+2m)/(m+6)`
`x+2y=1`
`<=>(2m-15)/(m+6)+(-18)/(m+6)=1`
`<=>(2m-33)/(m+6)=1`
`2m-33=m+6`
`<=>m=39(TM)`
Vậy `m=39` thì HPT có nghiệm duy nhất `x+2y=1`
b)Ta có: \(\left\{{}\begin{matrix}2x+my=-5\\x-3y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2+3y\\2\left(2+3y\right)+my=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2+3y\\6y+my+4=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3y+2\\y\left(m+6\right)=-9\end{matrix}\right.\)
Khi \(m\ne6\) thì \(y=-\dfrac{9}{m+6}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3y+2\\y=\dfrac{-9}{m+6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\cdot\dfrac{-9}{m+6}+2\\y=-\dfrac{9}{m+6}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-27}{m+6}+\dfrac{2m+12}{m+6}=\dfrac{2m-15}{m+6}\\y=\dfrac{-9}{m+6}\end{matrix}\right.\)
Để hệ phương trình có nghiệm duy nhất thỏa mãn x+2y=1 thì \(\dfrac{2m-15}{m+6}+\dfrac{-18}{m+6}=1\)
\(\Leftrightarrow2m-33=m+6\)
\(\Leftrightarrow2m-m=6+33\)
hay m=39
Vậy: Khi m=39 thì hệ phương trình có nghiệm duy nhất thỏa mãn x+2y=1
Cho hệ phương trình: \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\)
a/Với giá trị nào của k thì hệ phương trình có nghiệm là \(\left(x;y\right)=\left(2;-1\right)\)
b/Với giá trị nào của k thì hệ phương trình có nghiệm duy nhất?hệ phương trình vô nghiệm?
a) Ta có hệ phương trình \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\) Thay nghiệm \(\left(x,y\right)=\left(2,-1\right)\) ta có hệ mới là :
\(\hept{\begin{cases}2k-1=5\\2-1=1\end{cases}\Leftrightarrow k=3}\)
b) Ta có : \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1-x\\kx-1-x=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1-x\\x\left(k-1\right)=6\end{cases}}\)
Để hệ phương trình có nghiệm duy nhất : \(\Leftrightarrow k-1\ne0\) \(\Leftrightarrow k\ne1\)
Để hệ phương trình vô nghiệm \(\Leftrightarrow k-1=0\Leftrightarrow k=1\)
P/s : Em chưa học lớp 9 nên không biết cách trình bày cho lắm :))
Cho phương trình: x2 - 2 (m - 1)x - m - 3 = 0 (1)
1) Giải phương trình với m = -3
2) Tìm m để phương trình (1) có 2 nghiệm thoả mãn hệ thức \(x_1^2+x_2^2\) = 10.
3) Tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc giá trị của m
1, bạn tự giải
2,
\(\Delta'=\left(m-1\right)^2-\left(-m-3\right)=m^2-2m+1+m+3=m^2-m+4=\left(m-\dfrac{1}{2}\right)^2+\dfrac{15}{4}>0\)
Vậy pt luôn có 2 nghiệm x1 ; x2 khi \(\left(m-\dfrac{1}{2}\right)^2+\dfrac{15}{4}\ne0\left(luondung\right)\)
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-m-3\end{matrix}\right.\)
Ta có \(\left(x_1+x_2\right)^2-2x_1x_2=10\)
Thay vào ta được \(4\left(m-1\right)^2-2\left(-m-3\right)=10\)
\(\Leftrightarrow4m^2-8m+4+2m+6=10\Leftrightarrow4m^2-6m=0\)
\(\Leftrightarrow m\left(4m-6\right)=0\Leftrightarrow m=0;m=\dfrac{3}{2}\)
Cho hệ phương trình: a2x + y = 1 và x + y = a
a, giải hệ phương trình với a = -2
b, tìm các giá trị của a để hệ phương trình có vô số nghiệm
c, tìm a để hệ phương trình có nghiệm duy nhất (x,y) thỏa mãn x,y đều nguyên