Nêu hệ thức giữa U, I, R khi : R không đổi ; U không đổi
Viết các hệ thức thể hiện các tính chất của đoạn mạch nối tiếp, song song
Quan hệ U, I, R trong mạch điện hỗn hợp dạng (R1 nt Rb) // R2 và dạng (R1 // R2) nt Rb
Những câu hỏi liên quan
+ Nêu hệ thức giữa I, U, R khi: - R không đổi
- U không đổi
+ Quan hệ U, I, R trong đoạn mạch nối tiếp, song song, mạch điện hỗn hợp dạng ( R1 nt Rb)//R2 và dạng (R1 // R2) nt
+ C/m: Nếu R1 nt R2 => P=I^2 .Rtđ = P1 +P2;
Nếu R1 // R2 => P=U^2 /Rtđ = P1+P2
+ Cm :
Nếu : R1 ntR2
\(P=P_1+P_2=U_1I+U_2I=I.R_1.I+I.R_2.I=I^2R_1+I^2R_2=I^2\left(R_1+R_2\right)=I^2.R_{tđ}\)(I=I1 =I2)
Nếu : R1//R2
\(P=P_1+P_2=U.I_1+U.I_2=U.\frac{U}{R_1}+U\frac{U}{R_2}=\frac{U^2}{R_1}+\frac{U^2}{R_1}=U^2.\left(\frac{1}{R_1}+\frac{1}{R_2}\right)=U^2.\frac{1}{R_{tđ}}=\frac{U^2}{R_{tđ}}\)
(U=U1=U2)
Một đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm biến trở R mắc nối tiếp với cuộn cảm thuần có độ tự cảm L, đoạn mạch MB là tụ điện có điện dung C. Đặt điện áp xoay chiều
u
U
0
cos
2
π
f
t
(U không đổi, tần số f thay đổi được) vào hai đầu đoạn mạch AB. Khi tần số là
f
1
thì điện áp hiệu dụng trên R đạt cực đại. Khi...
Đọc tiếp
Một đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm biến trở R mắc nối tiếp với cuộn cảm thuần có độ tự cảm L, đoạn mạch MB là tụ điện có điện dung C. Đặt điện áp xoay chiều u = U 0 cos 2 π f t (U không đổi, tần số f thay đổi được) vào hai đầu đoạn mạch AB. Khi tần số là f 1 thì điện áp hiệu dụng trên R đạt cực đại. Khi tần số f 2 thì điện áp hiệu dụng giữa hai điểm AM là không đổi khi điều chỉnh R. Hệ thức liên hệ giữa f 1 và f 2
A. f 2 = 3 2 f 1
B. f 2 = 4 3 f 1
C. f 2 = 3 4 f 1
D. f 2 = f 1 2
Ta có ω 1 2 = 1 L C
Chuẩn hóa R = 1 Z L = x ⇒ Z C = x
Giả sử rằng tần số góc ω 2 = n ω 1 , khi đó ta có
U A M = U 1 2 + n x 2 1 2 + n x − x n 2 = U 1 + x 2 n 2 − 2 x 2 1 + n x 2
Để U A M không phụ thuộc vào R thì
x 2 n 2 − 2 x 2 = 0 ⇒ x = 0 n = 1 2 ⇒ f 2 = f 1 2
Đáp án D
Đúng 0
Bình luận (0)
Một đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm biến trở R mắc nối tiếp với cuộn cảm thuần có độ tự cảm L, đoạn mạch MB là tụ điện có điện dung C. Đặt điện áp xoay chiều uUsqrt{2}cosleft(2pi ftright) (U không đổi, tần số f thay đổi được) vào hai đầu đoạn mạch AB. Khi tần số là f1 thì điện áp hiệu dụng trên R đạt cực đại. Khi tần số là f2 thì điện áp hiệu dụng giữa hai điểm AM không thay đổi khi điều chỉnh R. Hệ thức liên hệ giữa f1 và f2 là:
Đọc tiếp
Một đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm biến trở R mắc nối tiếp với cuộn cảm thuần có độ tự cảm L, đoạn mạch MB là tụ điện có điện dung C. Đặt điện áp xoay chiều \(u=U\sqrt{2}\cos\left(2\pi ft\right)\) (U không đổi, tần số f thay đổi được) vào hai đầu đoạn mạch AB. Khi tần số là f1 thì điện áp hiệu dụng trên R đạt cực đại. Khi tần số là f2 thì điện áp hiệu dụng giữa hai điểm AM không thay đổi khi điều chỉnh R. Hệ thức liên hệ giữa f1 và f2 là:
trong trường hợp ban đầu
điện áp R cực đại nên tại f1 xảy ra hiện tượng cộng hưởng
\(Z_L=Z_C\)
\(LC=\frac{1}{\omega^2_1}\)
Trong trường hợp sau thì điện áp AM không đổi khi thay đổi R, lúc cố định tần số nghĩa là cảm kháng và dung kháng đều cố định
như vậy thì chỉ có trường hợp duy nhất là Uam bằng với U
Khi đó
\(Z_{LC}=Z_L=Z_C-Z_L\)
\(Z_C=2Z_L\)
\(LC=\frac{1}{2\omega^2_2}\)
Suy ra
\(\omega^2_1=2\omega^2_2\)
\(f_1=\sqrt{2}f_2\)
Đúng 0
Bình luận (0)
các công thức hệ thức cơ bản giữa các đại lượng điện U, I, R p, l, s, r(d), P, A, Q, t nêu rõ tên và đơn vị tính của chúng
Đặt điện áp xoay chiều
u
U
√
2
cos
(
ω
t
)
(
V
)
vào hai đầu đoạn mạch nối tiếp theo thứ tự: biến trở R, cuộn dây thuần cảm L và tụ điện có điện dung C thay đổi được. Khi C C1 thì điện áp hiệu dụng hai đầu biến trở không phụ thuộc vào giá trị của R. Khi C C2 thì điện áp hiệu dụng hai đầu đoạn mạch chứa L và R cũng không phụ thuộc vào R. Hệ thức liên h...
Đọc tiếp
Đặt điện áp xoay chiều u = U √ 2 cos ( ω t ) ( V ) vào hai đầu đoạn mạch nối tiếp theo thứ tự: biến trở R, cuộn dây thuần cảm L và tụ điện có điện dung C thay đổi được. Khi C = C1 thì điện áp hiệu dụng hai đầu biến trở không phụ thuộc vào giá trị của R. Khi C = C2 thì điện áp hiệu dụng hai đầu đoạn mạch chứa L và R cũng không phụ thuộc vào R. Hệ thức liên hệ giữa C1 và C2 là:
A. C 2 = 2 C 1
B. C 2 = 2 C 1
C. C 2 = 0 , 5 C 1
D. C 2 = C 1
+ C thay đổi để điện áp trên R không phụ thuộc vào R:
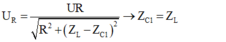
(cộng hưởng) thì điện áp hai đầu R luôn bằng U
+ C thay đổi để điện áp trên đoạn mạch LR không phục thuộc vào R:
→ Từ hai kết quả trên, ta thấy rằng:
Đúng 0
Bình luận (0)
Đặt điện áp xoay chiều uU
2
cos(ωt) V vào hai đầu đoạn mạch nối tiếp theo thứ tự: biến trở R, cuộn dây thuần cảm L và tụ điện có điện dung C thay đổi được. Khi C
C
1
thì điện áp hiệu dụng hai đầu biến trở không phụ thuộc vào giá trị của R. Khi C
C
2
thì điện áp hiệu dụng hai đầu đoạn mạch chứa L và R cũng không phụ thuộc vào R. Hệ thức liên hệ giữa
C...
Đọc tiếp
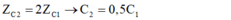
Đặt điện áp xoay chiều u=U 2 cos(ωt) V vào hai đầu đoạn mạch nối tiếp theo thứ tự: biến trở R, cuộn dây thuần cảm L và tụ điện có điện dung C thay đổi được. Khi C = C 1 thì điện áp hiệu dụng hai đầu biến trở không phụ thuộc vào giá trị của R. Khi C = C 2 thì điện áp hiệu dụng hai đầu đoạn mạch chứa L và R cũng không phụ thuộc vào R. Hệ thức liên hệ giữa C 1 và C 2 là:
A. C 2 = 2 C 1
B. C 2 = 2 C 1
C. C 2 = 0,5 C 1
D. C 2 = C 1
Đáp án C
Sử dụng giản đồ vecto trong dòng điện xoay chiều
Khi C = C 1 thì điện áp trên hai đầu R không phụ thuộc R, chứng tỏ có cộng hưởng. U R = U AB → Z C 1 = Z L
Khi C = C 2 thì điện áp trên hai đầu R L không phụ thuộc R, chứng tỏ U LR = U AB
Ta có giản đồ vecto
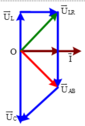
Từ giản đồ thấy được U C 2 = 2 U L
Đúng 0
Bình luận (0)
Đặt điện áp xoay chiều u U√2cos(ꞷt)V vào hai đầu đoạn mạch nối tiếp theo thứ tự: biến trở R, cuộn dây thuần cảm L và tụ điện có điện dung C thay đổi được. Khi C C1 thì điện áp hiệu dụng hai đầu biến trở không phụ thuộc vào giá trị của R. Khi C C2 thì điện áp hiệu dụng hai đầu đoạn mạch chứa L và R cũng không phụ thuộc vào R. Hệ thức liên hệ giữa C1 và C2 là A. C2 √2C1 B. C2 2C1 C. C2 0,5C1 D. C2 C1
Đọc tiếp
Đặt điện áp xoay chiều u = U√2cos(ꞷt)V vào hai đầu đoạn mạch nối tiếp theo thứ tự: biến trở R, cuộn dây thuần cảm L và tụ điện có điện dung C thay đổi được. Khi C = C1 thì điện áp hiệu dụng hai đầu biến trở không phụ thuộc vào giá trị của R. Khi C = C2 thì điện áp hiệu dụng hai đầu đoạn mạch chứa L và R cũng không phụ thuộc vào R. Hệ thức liên hệ giữa C1 và C2 là
A. C2 = √2C1
B. C2 = 2C1
C. C2 = 0,5C1
D. C2 = C1
Đặt điện áp xoay chiều
u
U
2
cos
(
ω
t
)
vào hai đầu đoạn mạch nối tiếp theo thứ tự: biến trở R, cuộn dây thuần cảm L và tụ điện có điện dung C thay đổi được. Khi C C1 thì điện áp hiệu dụng hai đầu biến trở không phụ thuộc vào giá trị của R. Khi C C2 thì điện áp hiệu dụng hai đầu đoạn mạch chứa L và R cũng không phụ thuộc vào R. Hệ thức liên hệ giữa C1 và C2 là A. ...
Đọc tiếp
Đặt điện áp xoay chiều u = U 2 cos ( ω t ) vào hai đầu đoạn mạch nối tiếp theo thứ tự: biến trở R, cuộn dây thuần cảm L và tụ điện có điện dung C thay đổi được. Khi C = C1 thì điện áp hiệu dụng hai đầu biến trở không phụ thuộc vào giá trị của R. Khi C = C2 thì điện áp hiệu dụng hai đầu đoạn mạch chứa L và R cũng không phụ thuộc vào R. Hệ thức liên hệ giữa C1 và C2 là
A. C 2 = 2 C 1
B. C 2 = 2 C 1
C. C 2 = 0 , 5 C 1
D. C 2 = C 1
Đáp án C
+ C thay đổi để điện áp trên R không phụ thuộc vào R:
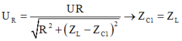
(cộng hưởng) thì điện áp hai đầu R luôn bằng U
+C thay đổi để điện áp trên đoạn mạch LR không phục thuộc vào R:
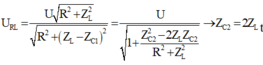
thì u R L không phụ thuộc vào R
→ Từ hai kết quả trên, ta thấy rằng Z C 2 = 2 Z C 1 → C 2 = 0 , 5 C 1
Đúng 0
Bình luận (0)
Đặt điện áp xoay chiều
u
U
2
cos
ω
t
V
vào hai đầu đoạn mạch nối tiếp theo thứ tự. biến trở R, cuộn dây thuần cảm L và tự điện có điện dung C thay đổi được. Khi C
C
1
thì điện áp hiệu dụng hai đầu biến trở không phụ thuộc vào giá trị...
Đọc tiếp
Đặt điện áp xoay chiều u = U 2 cos ω t V vào hai đầu đoạn mạch nối tiếp theo thứ tự. biến trở R, cuộn dây thuần cảm L và tự điện có điện dung C thay đổi được. Khi C = C 1 thì điện áp hiệu dụng hai đầu biến trở không phụ thuộc vào giá trị của R. Khi C = C 2 thì điện áp hiệu dụng hai đầu đoạn mạch chứa L và R cũng không phụ thuộc R. Hệ thức liên hệ giữa C 1 , C 2 là
A. C 2 = 0 , 5 C 1
B. C 2 = C 1
C. C 2 = 2 C 1
D. C 2 = 2 C 1
Đáp án A
+ Khi
C
=
C
1
Để U R không phụ thuộc R thì Z L 1 = Z C 1 => cộng hưởng điện.
+ Khi
C
=
C
2
: 
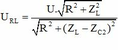
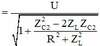
Để
U
R
L
không phụ thuộc R thì 
Suy ra 
Đúng 0
Bình luận (0)