cho đa thức p(x)+x^4+ax^2+bx+c chia hết cho đa thức (x-1)^3.hãy tìm a,b,c

Những câu hỏi liên quan
Xác định các hằng số a và b sao cho
a) x^4 + ax + b chia hết cho x^2 - 4
b) x^4 + ax^ + bx - 1 chia hết cho x^2 - 1
c) x^3 + ax + b chia hết cho x^2 + 2x - 2
(Chia đa thức cho đa thức)

Chỉ ý kiến của mk thôi
chưa chắc đúng
Tham khảo nhé
Đúng 0
Bình luận (0)
Tìm a,b sao cho:
a,Đa thức x^4-x^3+6x^2-x+a chia hết cho x^2-x+5
b,Đa thức 2x^3-3x^2+x+a chia hết cho x+2
c,Đa thức 3x^3+ax^2+bx+9 chia hết cho x+3 và x-3
Cau a va b dat cot tim so du .Vi la phep chia het nen du bang 0.Cau c thi da thuc se chia het cho tich (x+3)(x-3) lam tuong tu hai cau a va b
Đúng 0
Bình luận (2)
Tìm các hệ số a,b,c sao cho đa thức 3x^4+ax^2+bx+c chia hết cho đa thức (x-2) và chia cho đa thức (x^2-1) được thương và còn dư (-7x-1)
1. Tìm các số thực a,b để đa thức P (x) = x3 + ax2 + bx + 4 chia hết cho đa thức (x - 2)2
2. Tìm các số thực a,b để đa thức P (x) = x3 + x2 + ax + 4 chia hết cho đa thức x2 + 1
tìm các hệ số a,b,c sao cho đa thức \(3x^4+ax^2+bx+c\) chi hết cho đơn thức x-2 và chia cho đa thức \(x^2-1\) dư -7x-1
Tìm các hệ số a,b,c sao cho đa thức 3x^4 ax^2 bx c chia hết cho đa thức x-2?
Xem chi tiết
Tìm a,b sao cho:
a,Đa thức x^4-x^3+6x^2-x+a chia hết cho x^2-x+5
b,Đa thức 2x^3-3x^2+x+a chia hết cho x+2
c,Đa thức 3x^3+ax^2+bx+9 chia hết cho x+3 và x-3
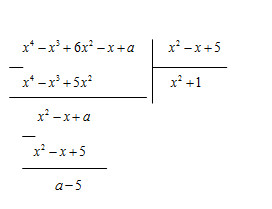
Vậy a = 5 thì đa thức x^4 - x^3 + 6x^2 - x +a chia hết cho đa thức x^2 - x + 5
Đúng 0
Bình luận (0)
Xác định các hệ số a, b, c sao cho đa thức: \(f\left(x\right)=2x^4+ax^2+bx+c\) chia hết cho đa thức x-2 và khi chia cho đa thức: \(x^2-1\) thì có dư là x
Vì \(f\left(x\right)⋮x-2;f\left(x\right):x^2-1\) dư 1\(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)=g\left(x\right)\cdot\left(x-2\right)\\f\left(x\right)=q\left(x\right)\left(x^2-1\right)+x=q\left(x\right)\left(x-1\right)\left(x+1\right)+x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}f\left(2\right)=0\\f\left(1\right)=1\\f\left(-1\right)=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}32+4a+2b+c=0\\2+a+b+c=1\\2+a-b+c=-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}4a+2b+c=-32\left(1\right)\\a+b+c=-1\left(2\right)\\a-b+c=-3\left(3\right)\end{matrix}\right.\)
Trừ từng vế của (2) cho (3) ta được:
\(\Rightarrow2b=2\Rightarrow b=1\)
Thay b=1 vào lần lượt (1) ,(2),(3) ta được:
\(\Rightarrow\left\{{}\begin{matrix}4a+2+c=-32\\a+1+c=-1\\a-1+c=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a+c=-34\\a+c=-2\\a+c=-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4a+c=-34\left(4\right)\\a+c=-2\left(5\right)\end{matrix}\right.\)
Trừ từng vế của (4) cho (5) ta được:
\(\Rightarrow3a=-32\Rightarrow a=-\dfrac{32}{3}\Rightarrow c=-2+\dfrac{32}{3}=\dfrac{26}{3}\) Vậy...
Đúng 2
Bình luận (0)
Cho đa thức f(x)=x4+ax3+bx-1. Tìm a,b để đa thức f(x) chia hết cho x2-3x+2
Đa thức x2 - 3x + 2 có nghiệm \(\Leftrightarrow\)x2 - 3x + 2 = 0
\(\Leftrightarrow x^2-2x-x+2=0\)
\(\Leftrightarrow x\left(x-2\right)-\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=1\\x=2\end{cases}}\)
1 và 2 là hai nghiệm của đa thức x2 - 3x + 2
Để f(x) = x4 + ax3 + bx - 1 chia hết cho x2 - 3x + 2 thì 1 và 2 cũng là hai nghiệm của đa thức f(x) = x4 + ax3 + bx - 1
Nếu x = 1 thì \(1+a+b-1=0\Leftrightarrow a+b=0\)(1
Nếu x = 2 thì \(16+8a+2b-1=0\Leftrightarrow4a+b=\frac{-15}{2}\)(2)
Lấy (2) - (1), ta được: \(3a=\frac{-15}{2}\Leftrightarrow a=\frac{-5}{2}\)
\(\Rightarrow b=0+\frac{5}{2}=\frac{5}{2}\)
Vậy \(a=\frac{-5}{2};b=\frac{5}{2}\)





 Chào bạn!
Chào bạn!










