Cho đường tròn tâm O đường kính AB , qua trung điểm I của bán kính OA kẻ dây MN vuông góc với OA
a) Tứ giác OMAN là hình gì ? Vì sao ?
b) Tam giác BMN là tam giác gì ? Vì sao
Những câu hỏi liên quan
Cho đường tròn tâm O bán kính R , đường kính AB . Dây cung CD vuông góc với OA tại M , M là trung điểm của OA.
a) Tứ giác ACOD là hình gì ? Vì sao ?
b) Tam giác ACD là tam giác gì ? Vì sao ?
BT1: Cho đường tròn tâm O, đường kính AB. Dây CD cắt AB tại M biết MC= 4cm, MD= 12cm, góc BMD= 30 độ
a/ Tính khoảng cách từ O đến CD
b/ Tính bán kính đường tròn O
BT2: Cho đường tròn tâm O bán kính R, đường kính AB, dây CD vuông góc với OA tại điểm M là trung điểm của OA
a/ Tứ giác ACOD là hình gì ? Vì sao?
b/ Tam giác BCD là tam giác gì ? Vì sao ?
Cho đường tròn (O;R) đường kính AD. Dây BC vuông góc với OA tại trung điểm I của OA.
a. Tứ giác ABOC là hình gì? Vì sao?
b. Tam giác BCD là tam giác gì? Vì sao?
Cho đường tròn (O) bán kính OA = R. Qua trung điểm của OA, kẻ dây BC vuông góc với OA.
a. Tứ giác ABOC là hình gì? Vì sao?
b. trên tia OA lấy điểm E sao cho OE = 2R. Chứng minh BE là tiếp tuyến của đường tròn (O)
a: Gọi H là trung điểm của OA
Xét (O) có
OH là một phần đường kính
BC là dây
OH⊥BC tại H
Do đó: H là trung điểm của BC
Xét tứ giác ABOC có
H là trung điểm của đường chéo AO
H là trung điểm của đường chéo BC
Do đó: ABOC là hình bình hành
mà OB=OC
nên ABOC là hình thoi
Đúng 0
Bình luận (0)
Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.
Tứ giác OCAB là hình gì? Vì sao?
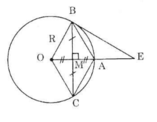
Bán kính OA vuông góc với BC nên MB = MC.
Lại có MO = MA (gt).
Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.
Lại có: OA ⊥ BC nên OBAC là hình thoi.
Đúng 0
Bình luận (0)
Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.
a) Tứ giác OCAB là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.
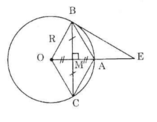
a) Bán kính OA vuông góc với BC nên MB = MC.
Lại có MO = MA (gt).
Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.
Lại có: OA ⊥ BC nên OBAC là hình thoi.
b) Ta có: OA = OB (bán kính)
OB = BA (tính chất hình thoi).
Nên OA = OB = BA => ΔAOB đều = > ∠ A O B = 60 °
Trong tam giác OBE vuông tại B ta có:
B E = O B . t g ∠ A O B = O B . t g 60 ° = R . √ 3
Đúng 0
Bình luận (0)
Cho đường tròn tâm O có bán kính OA R, dây BC vuông góc vói OA tại trung điểm M của OAa, Tứ giác OCAB là hình gì? Vì sao?b, Kẻ tiếp tuyến với đường tròn tại B, cắt đường thẳng OA tại E. Tính độ dài BE theo R
Đọc tiếp
Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc vói OA tại trung điểm M của OA
a, Tứ giác OCAB là hình gì? Vì sao?
b, Kẻ tiếp tuyến với đường tròn tại B, cắt đường thẳng OA tại E. Tính độ dài BE theo R
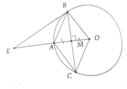
a, OA vuông góc với BC tại M
=> M là trung điểm của BC
=> OCAB là hình thoi
b, Tính được BE = R 3
Đúng 0
Bình luận (0)
Cho đường tròn tâm (O);bán kính R;đường kính AB;dây CD vuông góc OA tại M
a,Tứ giác ACOD là hình gì ? Ví sao?
b,Tam giác BCD là tam giác gì?Vì sao?
c,Cho R=4.Tính chu vi và diện tích ABCD
Cho đường tròn (O) bán kính OA = R Vẽ dây BC vuông góc với OA tại trung điểm H của OA.
a) Tứ giác ABOC là hình gì? Vì sao?
b) Gọi K là điểm đối xứng với O qua A Chứng minh rằng K, B, O, C cùng thuộc một đường tròn
a: Xét tứ giác ABOC có
H là trung điểm của OA
H là trung điểm của BC
Do đó: ABOC là hình bình hành
mà OA=OB
nên ABOC là hình thoi
Đúng 1
Bình luận (0)
Cho đường tròn (O), đường kính AD vuông góc với dây BC tại I (I thuộc bán kính OD) a) ΔABC là tam giác gì? Vì sao? b) Kẻ BE vuông góc với AC (E thuộc AC), BE cắt AD ở H. Chứng minh BH//CD c) Tứ giác BHCD là hình gì? Vì sao? d) Gọi O' là tâm đường tròn bán kính AH. Chứng minh rằng điểm E nằm trên đường tròn (O') e) Chứng muinh rằng IE là tiếp tuyến của đường tròn (O')