tìm x
8x3 - 12x2 + 8x - 1 = 0
Với mỗi phương trình sau, đã biết một nghiệm (ghi kèm theo), hãy tìm nghiệm kia:
12 x 2 - 8 x + 1 = 0 ; x 1 = 1 2
Theo định lý Vi-et ta có: phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2 thì: 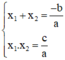
Ta sử dụng một trong hai biểu thức trên để tìm nghiệm còn lại.
Ở bài giải dưới đây ta sẽ sử dụng điều kiện: 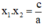
(Các bạn có thể làm cách 2 sử dụng điều kiện 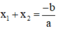 ).
).
Ta có: x 1 . x 2 = c a
Với mỗi phương trình sau, đã biết một nghiệm (ghi kèm theo), hãy tìm nghiệm kia:
a ) 12 x 2 − 8 x + 1 = 0 ; x 1 = 1 2 b ) 2 x 2 − 7 x − 39 = 0 ; x 1 = − 3 c ) x 2 + x − 2 + 2 = 0 ; x 1 = − 2 d ) x 2 − 2 m x + m − 1 = 0 ; x 1 = 2
Theo định lý Vi-et ta có: phương trình
a
x
2
+
b
x
+
c
= 0 có hai nghiệm
x
1
;
x
2
thì: 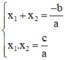
Ta sử dụng một trong hai biểu thức trên để tìm nghiệm còn lại.
Ở bài giải dưới đây ta sẽ sử dụng điều kiện: 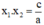
(Các bạn có thể làm cách 2 sử dụng điều kiện 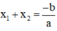 ).
).
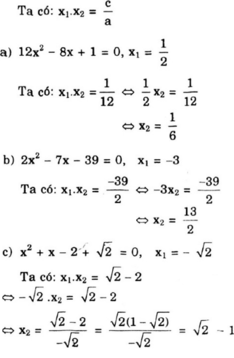
d) x 2 - 2 m x + m - 1 = 0 ( 1 )
Vì x 1 = 2 là một nghiệm của pt (1) nên:
2 2 - 2 m . 2 + m - 1 = 0
⇔ 4- 4 m+ m – 1 = 0
⇔ 3- 3m = 0
⇔ m = 1
Khi m = 1 ta có: x 1 . x 2 = m - 1 (hệ thức Vi-ét)
⇔ 2 . x 2 = 0 ( v ì x 1 = 2 và m = 1)
⇔ x 2 = 0
Tính giá trị của phân thức:
a) x 2 − 1 2 x 2 − 3 x + 1 với x ≠ 1 và x ≠ 1 2 tại 2 x + 1 = 3 ;
b) 3 x 2 − 10 x + 3 x 2 − 4 x + 3 với x ≠ 2 ; x ≠ 3 tại x 2 − 8 x + 15 = 0 .
Bài 1 :Phân tích đa thức sau thành nhân tử
(12x2+6x)(y+z)+(12x2+6x)(y-z)
Bài 2:tìm x:
x(x-6)+10(x-6)=0
1.
\(\left(12x^2+6x\right)\left(y+z\right)+\left(12x^2+6x\right)\left(y-z\right)\\ =\left(12x^2+6x\right)\left(y+z+y-z\right)\\ =2y\left(12x^2+6x\right)\\ =2y.6x\left(2x+1\right)\\ =12xy\left(2x+1\right)\)
2.
\(x\left(x-6\right)+10\left(x-6\right)=0\\ \Leftrightarrow\left(x-6\right)\left(x+10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-10\end{matrix}\right.\)
Vậy \(x\in\left\{6;-10\right\}\) là nghiệm của pt
Bài 1:
Ta có: \(\left(12x^2+6x\right)\left(y+z\right)+\left(12x^2+6x\right)\left(y-z\right)\)
\(=\left(12x^2+6x\right)\left(y+z+y-z\right)\)
\(=6x\left(2x+1\right)\cdot2y\)
\(=12xy\left(2x+1\right)\)
Bài 2:
Ta có: \(x\left(x-6\right)+10\left(x-6\right)=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-10\end{matrix}\right.\)
Tìm x biết ( 2 x 4 – 3 x 3 + x 2 ) : - 1 2 x 2 + 4 ( x – 1 ) 2 = 0
A. x = -1
B. x = 2
C. x = 1
D. x = 0
Ta có
( 2 x 4 – 3 x 3 + x 2 ) : - 1 2 x 2 + 4 ( x – 1 ) 2 = 0 ⇔ 2 x 4 : ( - 1 2 x 2 ) - 3 x 3 : ( - 1 2 x 2 ) + x 2 : ( - 1 2 x 2 ) + 4 ( x 2 - 2 x + 1 ) = 0 ⇔ - 4 x 2 + 6 x – 2 + 4 x 2 – 8 x + 4 = 0
ó -2x + 2 = 0
ó x = 1
Đáp án cần chọn là: C
tìm x biết a) ( x + 3 )2 - ( 2x + 1 ).( x+3 ) = 0 ; b) x3 - 12x2 + 36x = 0
\(a,\Leftrightarrow\left(x+3\right)\left(x+3-2x-1\right)=0\\ \Leftrightarrow\left(x+3\right)\left(2-x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\\ b,\Leftrightarrow x\left(x^2-12x+36\right)=0\\ \Leftrightarrow x\left(x-6\right)^2=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
a, (x+3)2 - ( 2x + 1 ).( x+3)=0 b, x3-12x2+36x =0
=> (x+3).(x+3-2x-1) => x(x2-12x+36) = 0
=>(x+3).(-x+2) => x(x-6)2 = 0
=> x+3=0 <=> x=-3 => x=0 <=> x=0
-x+2=0 <=> x=-2 x-6= 0 <=> x=6
Tìm a để: g(x)=x4+5x3-12x2+8x+a chia hết cho x+1
phân tích đa thức thành nhân tử
a) 1+6x-6x2-x3
b) x3-4x2+8x-8
c) x3+2x2+2x+1
d) 8x3-12x2+6x-1
a) Ta có: \(1+6x-6x^2-x^3\)
\(=\left(1-x\right)\left(x^2+x+1\right)+6x\left(1-x\right)\)
\(=\left(1-x\right)\left(x^2+7x+1\right)\)
b:Ta có: \(x^3-4x^2+8x-8\)
\(=\left(x-2\right)\left(x^2+2x+4\right)-4x\left(x-2\right)\)
\(=\left(x-2\right)\left(x^2-2x+4\right)\)
c: Ta có: \(x^3+2x^2+2x+1\)
\(=\left(x+1\right)\left(x^2-x+1\right)+2x\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+x+1\right)\)
d: Ta có: \(8x^3-12x^2+6x-1\)
\(=\left(2x\right)^3-3\cdot\left(2x\right)^2\cdot1+3\cdot2x\cdot1^2-1^3\)
\(=\left(2x-1\right)^3\)
Giải phương trình 3 x 2 + 2 x + 4 = 8 x 3 + 12 x 2 + 8 x + 1 3 x 2 + 2 x + 5
Ta có: 3 x 2 + 2 x + 4 = 8 x 3 + 12 x 2 + 8 x + 1 3 x 2 + 2 x + 5 = ( 2 x + 1 ) 3 + 2 x + 1 3 x 2 + 2 x + 5 (1)
Dễ thấy 3 x 2 + 2 x + 4 > 0 với mọi x. Đặt u = 3 x 2 + 2 x + 4 v = 2 x + 1 .
Ta có: ( 1 ) ⇔ u = v 3 + v u 2 + 1 ⇔ u 3 + u = v 3 + v ⇔ ( u − v ) ( u 2 + u v + v 2 + 1 ) = 0 ⇔ u = v
(Vì u 2 + u v + v 2 + 1 = u + v 2 2 + 3 4 v 2 + 1 > 0 )
u = v ⇔ 3 x 2 + 2 x + 4 = 2 x + 1 ⇒ 3 x 2 + 2 x + 4 = 4 x 2 + 4 x + 1 x 2 − 2 x − 3 = 0 ⇒ x = 3 h o a c x = − 1.
Thử lại, ta nhận x= 3
Tìm x biết x 3 – 12 x 2 + 48 x – 64 = 0
A. x = -4
B. x = 4
C. x = -8
D. x = 8
Ta có
x 3 – 12 x 2 + 48 x – 64 = 0 ⇔ x 3 – 3 . x 2 . 4 + 3 . x . 4 2 – 4 3 = 0 ⇔ ( x – 4 ) 3 = 0
ó x – 4 = 0 ó x = 4
Vậy x = 4
Đáp án cần chọn là: B