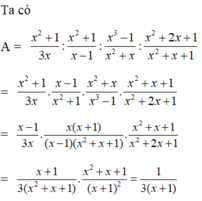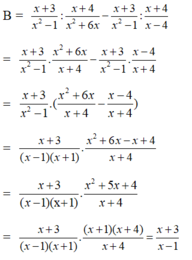1, Với x \(_{\le}\)1, hãy so sánh √x - √x-1 và √x+1 -√x

Những câu hỏi liên quan
Cho biểu thức \(P=\left(\dfrac{\sqrt{x}}{x\sqrt{x}-1}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\); \(x\ge0,x\ne1\).
a) Rút gọn P.
b) Tìm x để \(P=\sqrt{x}\).
c) Với x > 1, hãy so sánh P và \(\sqrt{P}\).
a) Ta có: \(P=\left(\dfrac{\sqrt{x}}{x\sqrt{x}-1}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}+x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{x+\sqrt{x}+1}{\sqrt{x}+1}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
Đúng 1
Bình luận (0)
Cho A
x
2
+
1
3
x
:
x
2
+
1
x
−
1
:
x
3
−
1...
Đọc tiếp
Cho A = x 2 + 1 3 x : x 2 + 1 x − 1 : x 3 − 1 x 2 + x : x 2 + 2 x + 1 x 2 + x + 1 và B = x + 3 x 2 − 1 : x + 4 x 2 + 6 x − x + 3 x 2 − 1 : x + 4 x − 4 . Khi x = 101, hãy so sánh A và B.
A. B < A
B. B > A
C.B = A
D. B ≤ A
1. Cho biểu thức P= \(\left(\frac{\sqrt{x}}{x\sqrt{x}-1}+\frac{1}{\sqrt{x}-1}\right):\frac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
a, Rút gọn và tìm ĐKXĐ.
b, Với x>1 hãy so sánh P với \(\sqrt{P}\).
a, \(P=\left(\frac{\sqrt{x}}{x\sqrt{x}-1}+\frac{1}{\sqrt{x}-1}\right):\frac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\left(\frac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\frac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right):\frac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\frac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\frac{x+\sqrt{x}+1}{\sqrt{x}+1}=\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
b, Vì x > 1, g/s : Thay x = 4 vào P ta được :
\(\frac{\sqrt{4}+1}{\sqrt{4}-1}=\frac{3}{1}=3\)
Thay x = 4 vào căn P ta được : \(\sqrt{\frac{\sqrt{4}+1}{\sqrt{4}-1}}=\sqrt{3}\)
mà \(3>\sqrt{3}\Rightarrow P>\sqrt{P}\)với x > 1
Cho x=a/b; y= c/d; z= m/n
Trong đó m= (a+c)/2; n= (b+d)/2
a) Biết x khác y hãy so sánh x với z và y với z
b) Hãy so sánh y với t biết t= a+m/b+m và ad - bc= 1; cn - dm = 1
cho x thuộc Z. Hãy so sánh 19.(x-1) và 14.(x-15)
hãy so sánh :
1+ (x + x + ... + x).x và xn-1 + (2-x)
n số x
So Sánh
{eq \x\le\ri(X+\(\frac{1}{3}\))}.+\(\frac{1}{4}\)với \(\frac{1}{5}\)
\(P=\left(\frac{2x}{x^2-1}+\frac{x-1}{2x+2}\right):\frac{x+1}{2x}\)
a. tìm điều kiện xác định của P và rút gọn P
b. tìm x để P =2
c. với 0 < x < 1 . hãy so sánh P với |P|
a. tìm điều kiện xác định của P
ĐKXĐ: \(x\ne0;x\ne\pm1\)
\(P=\left(\frac{2x}{\left(x-1\right)\left(x+1\right)}+\frac{x-1}{2\left(x+1\right)}\right):\frac{x+1}{2x}\)
\(P=\frac{4x+\left(x-1\right)^2}{2\left(x-1\right)\left(x+1\right)}\times\frac{2x}{x+1}\)
\(P=\frac{4x+x^2-2x+1}{2\left(x-1\right)\left(x+1\right)}\times\frac{2x}{x+1}\)
\(P=\frac{x^2+2x+1}{\left(x-1\right)\left(x+1\right)}\times\frac{x}{x+1}\)
\(P=\frac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}\times\frac{x}{x+1}\)
\(P=\frac{x}{x-1}\)
b. tìm x
Với P = 2 ta có:
\(\frac{x}{x-1}=2\)
=> x = 2(x-1)
=> x = 2x -2
=> 2x - x = 2
=> x = 2
Vậy với x = 2 thì P = 2
c. với 0 < x < 1 . hãy so sánh P với |P|
\(P=\frac{x}{x-1}\)
Với 0< x < 1 thì x -1 <0 ; x>0 => P <0
Suy ra P< |P| ( vì |P| >0)
Câu hỏi tương tự Đọc thêm Báo cáoToán lớp 8
Đúng 0
Bình luận (0)
A. DE P XAC DINH
<=>X^2-1 KHÁC 0<=>X KHAC -1 VÀ X KHÁC 1
<=>2X+2 KHAC 0 <=>X KHAC-1
<=>2X KHAC 0 <=>X KHAC 0
=> X KHAC O HOAC X KHAC +-1
TACO:( 2X / X^2-1 +X-1/ 2X+2 ) : X+1 / 2X
=[2X . 2 / (X+1)(X-1). 2 + (X-1)(X-1) / 2(X+1)(X-1) ] : X+1/2X
=[4X+(X-1)^2] / 2(X+1)(X-1) :X+1 / 2X
=(4X+X^2-2X+1) / 2(X+1)(X-1) : X+1/2X
=X^2+2X+1 / 2(X-1)(X+1) : X+1 / 2X
=(X+1)^2 / 2(X-1)(X+1) : X+1/2X
=(X+1) / 2(X-1) . 2X/X+1
=X/X-1
B. DE P=2
<=>X/X-1=2
<=>X=2(X-1)=2X-2=X+X-2
TA CÓ: X +X-2 = X+0
=>X-2=0
=>X=2
C .VI 0<X<1
=>X / X-1 = |X/X-1|
=>P=|P|
Đúng 0
Bình luận (0)
Không tính hãy so sánh A và B
A=1990 x 2010 + 1 và B=2000 x 2000+1
ta có: A = 1990 x 2010 + 1 = 1990 x 2000 + 1990 x 10 + 1 = 1 990 x 2000 + 19 900 + 1
B = 2000 x 2000 + 1 = 2000 x 1990 + 2000 x 10 +1 = 2000 x 1990 + 20 000 + 1 > 1 990 + 2000 + 19 000 + 1
=> A < B
Đúng 0
Bình luận (0)
Cho biểu thức:
A=\(\left(\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}-\dfrac{3x+\sqrt{x}}{\sqrt{x}}+2\right):\dfrac{\left(\sqrt{x}+1\right)^2-4\sqrt{x}}{x-\sqrt{x}}\)
a) Rút gọn A
b) Với x>1 hãy so sánh |A| với A
c) Tìm x để A=5
d) tìm min của A