Cho biểu thức P=2a2 +9a-6
Tìm giá trị nhỏ nhất của biểu thức P
Những câu hỏi liên quan
Tìm giá trị nhỏ nhất của các biểu thức sau:
C = 2a2 + b2 - 2ab + 10a + 42.
C=2a2+b2-2ab+10a+42
=a2-2ab+b2+a2+10a+25+17
=(a-b)2+(a+5)2+17
=>MIN(C)=17 <=>a-b=0 và a+5=0
<=>a=b=-5
vậy ..................
Đúng 1
Bình luận (0)
cho biểu thức P = 2014+ 540 : ( x - 6)
tìm giá trị của x để biểu thức P có giá trị lớn nhất, nhỏ nhất
tìm giá trị lớn nhất, nhỏ nhất đó
- p lon nhat khi x = 7 , p nho nhat khi x = 6
- p lon nhat = 2554 , p nho nhat = 2014
dung khong ta ?
Cho biểu thức P=2014+540:(x-6)
Tìm giá trị của x để biểu thức P có giá trị lớn nhất ,nhỏ nhất
Tìm giá trị lớn nhất nhỏ nhất đó
Cho biểu thức P=2014+540:(x-6)
Tìm giá trị của x để biểu thức P có giá trị lớn nhất ,nhỏ nhất
Tìm giá trị lớn nhất,nhỏ nhất đó
Cho A=\(\frac{39,48X17+83X39,48}{1990-72:9a-\left(a-6\right)}\)
a. TÍnh giá trị của biểu thức A khi a = 51.
b. Tìm giá trị số tự nhiên của a để biểu thức A có giá trị lớn nhất.
Cho các biểu thức A=\(\dfrac{6}{x-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\) và B=\(\dfrac{3}{\sqrt{x}-1}\) với x≥0, x≠1, x≠9
a) Tính giá trị của B khi x=4
b) Rút gọn biểu thức P=A-B
c) Tìm xϵN để biểu thức \(\dfrac{1}{P}\) đạt giá trị lớn nhất
a) Thay x=4 vào biểu thức \(B=\dfrac{3}{\sqrt{x}-1}\), ta được:
\(B=\dfrac{3}{\sqrt{4}-1}=\dfrac{3}{2-1}=3\)
Vậy: Khi x=4 thì B=3
b) Ta có: P=A-B
\(\Leftrightarrow P=\dfrac{6}{x-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{3}{\sqrt{x}-1}\)
\(\Leftrightarrow P=\dfrac{6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{6+x-\sqrt{x}-3\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{x-\sqrt{x}-3\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)-3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
Đúng 4
Bình luận (0)
1) Cho biểu thức A=2006-x/6-x. tìm giá trị nguyên của x để A đạt giá trị lớn nhất. tìm giá trị lớn nhất đó.
2) tìm giá trị nhỏ nhất của biểu thức: P=4-x/14-x;(x thuộc Z). khi đó x nhận giá trị nguyên nào ?
tach 14-x = 10-4-x roi sau do chac ban cung phai tu biet lam
Đúng 0
Bình luận (0)
Xét phương trình ax3- x2+ bx-10 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức
P
5
a
2
-
3
a
b
+
2
a
2
(
b
-...
Đọc tiếp
Xét phương trình ax3- x2+ bx-1=0 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 - 3 a b + 2 a 2 ( b - a ) .
A. 15 3
B. 8 2
C. 11 6
D. 12 3
Giả sử phương trình đã cho có 3 nghiệm
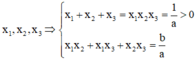
Khi đó
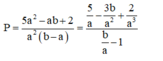
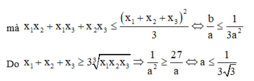
Suy ra
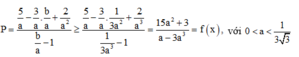
Xét hàm số:
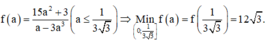
Chọn D.
Đúng 0
Bình luận (0)
a) Tìm x sao cho giá trị biểu thức dfrac{3x-2}{4}không nhỏ hơn giá trị của biểu thức dfrac{3x+3}{6}b) Tìm x sao cho giá trị của biểu thức (x+1)2 nhỏ hơn giá trị của biểu thức (x-1)2.c) Tìm x sao cho giá trị của biểu thức dfrac{2x-3}{35}+dfrac{xleft(x-2right)}{7} không lớn hơn giá trị của biểu thức dfrac{x^2}{7}-dfrac{2x-3}{5}
Đọc tiếp
a) Tìm x sao cho giá trị biểu thức \(\dfrac{3x-2}{4}\)không nhỏ hơn giá trị của biểu thức \(\dfrac{3x+3}{6}\)
b) Tìm x sao cho giá trị của biểu thức (x+1)2 nhỏ hơn giá trị của biểu thức (x-1)2.
c) Tìm x sao cho giá trị của biểu thức \(\dfrac{2x-3}{35}+\dfrac{x\left(x-2\right)}{7}\) không lớn hơn giá trị của biểu thức \(\dfrac{x^2}{7}-\dfrac{2x-3}{5}\)
a: Để \(\dfrac{3x-2}{4}\) không nhỏ hơn \(\dfrac{3x+3}{6}\) thì \(\dfrac{3x-2}{4}>=\dfrac{3x+3}{6}\)
=>\(\dfrac{6\left(3x-2\right)}{24}>=\dfrac{4\left(3x+3\right)}{24}\)
=>18x-12>=12x+12
=>6x>=24
=>x>=4
b: Để \(\left(x+1\right)^2\) nhỏ hơn \(\left(x-1\right)^2\) thì \(\left(x+1\right)^2< \left(x-1\right)^2\)
=>\(x^2+2x+1< x^2-2x+1\)
=>4x<0
=>x<0
c: Để \(\dfrac{2x-3}{35}+\dfrac{x\left(x-2\right)}{7}\) không lớn hơn \(\dfrac{x^2}{7}-\dfrac{2x-3}{5}\) thì
\(\dfrac{2x-3}{35}+\dfrac{x\left(x-2\right)}{7}< =\dfrac{x^2}{7}-\dfrac{2x-3}{5}\)
=>\(\dfrac{2x-3+5x\left(x-2\right)}{35}< =\dfrac{5x^2-7\cdot\left(2x-3\right)}{35}\)
=>\(2x-3+5x^2-10x< =5x^2-14x+21\)
=>-8x-3<=-14x+21
=>6x<=24
=>x<=4
Đúng 0
Bình luận (0)