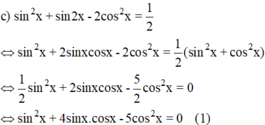
+ Xét cos x = 0 ⇒ sin2x = 1 – cos2x = 1

(1) trở thành 1 = 0 (Vô lý).

+ Xét cos x ≠ 0, chia cả hai vế cho cos2x ta được:

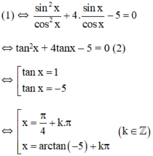
Vậy phương trình có tập nghiệm 

 (k ∈ Z)

3sin2x – 4sinx.cosx + 5cos2x = 2

⇔ 3sin2x – 4sinx.cosx + 5cos2x = 2(sin2x + cos2x)

⇔ sin2x – 4sinx.cosx + 3 cos2x = 0 (1)

+ Xét cosx = 0 ⇒ sin2x = 1.

Phương trình (1) trở thành 1 = 0 (Vô lý).

+ Xét cos x ≠ 0. Chia hai vế phương trình cho cos2x ta được

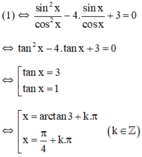
Vậy phương trình có tập nghiệm 

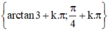 (k ∈ Z)

Đặt \(\dfrac{x}{4}=t\)

\(2sin^22t-3cost=0\)

\(\Leftrightarrow8sin^2t.cos^2t-3cost=0\)

\(\Leftrightarrow8cos^2t\left(1-cos^2t\right)-3cost=0\)

\(\Leftrightarrow-8cos^4t+8cos^2t-3cost=0\)

\(\Leftrightarrow-cost\left(8cos^3t-8cost+3\right)=0\)

\(\Leftrightarrow cost\left(2cost-1\right)\left(4cos^2t+2cost-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cost=0\\cost=\dfrac{1}{2}\\cost=\dfrac{-1+\sqrt{13}}{4}\\cost=\dfrac{-1-\sqrt{13}}{4}< -1\left(loại\right)\end{matrix}\right.\)

\(\Leftrightarrow...\)

\(\Leftrightarrow2cos2x.cos\left(\dfrac{\pi}{6}\right)-2sin2x.sin\left(\dfrac{\pi}{6}\right)+2sin2x-1=0\)

\(\Leftrightarrow\sqrt{3}cos2x+sin2x=1\)

\(\Leftrightarrow\dfrac{\sqrt{3}}{2}cos2x+\dfrac{1}{2}sin2x=\dfrac{1}{2}\)

\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{6}=\dfrac{\pi}{3}+k2\pi\\2x-\dfrac{\pi}{6}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow...\)

\(pt\Leftrightarrow\left(\frac{4}{x^2}+\frac{x^2}{4-x^2}\right)+\frac{5}{2}\left(\frac{\sqrt{4-x^2}}{x}+\frac{x}{\sqrt{4-x^2}}\right)+2=0\)

\(\Leftrightarrow\left(\frac{\sqrt{4-x^2}}{x}+\frac{x}{\sqrt{4-x^2}}\right)^2-1+\frac{5}{2}\left(\frac{\sqrt{4-x^2}}{x}+\frac{x}{\sqrt{4-x^2}}\right)+2=0\)

Đặt \(\frac{\sqrt{4-x^2}}{x}+\frac{x}{\sqrt{4-x^2}}=t\)pt thành

\(t^2-1+\frac{5}{2}t+2=0\)\(\Rightarrow\orbr{\begin{cases}t=-2\\t=-\frac{1}{2}\end{cases}}\)(loại)

-->PT vô nghiệm

\(\frac{3}{x^2}\)hay\(\frac{4}{x^2}\)

Thắng Nguyễn \(\frac{4}{x^2}\) . T làm ra r , you k cần làm nữa đâu , thanks :))