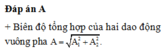Cho hai dao động điều hòa cùng phương với các phương trình lần lượt là x1 = A1cos(ωt + 0.35) cm và x2 = A2cos(ωt + 1.57) cm. Dao động tổng hợp của hai dao động này có phương trình là x = 20cos(ωt + φ). Giá trị cực đại của 3A1 + 2A2?

Những câu hỏi liên quan
Cho hai dao động điều hòa cùng phương với các phương trình lần lượt là
x
1
A
1
cos
(
ω
t
+
0
,
35
)
(cm) và
x
2
A
2
cos
(
ω
t
-
1
,
75
)
) (cm). Dao động tổng hợp của hai dao động n...
Đọc tiếp
Cho hai dao động điều hòa cùng phương với các phương trình lần lượt là x 1 = A 1 cos ( ω t + 0 , 35 ) (cm) và x 2 = A 2 cos ( ω t - 1 , 75 ) ) (cm). Dao động tổng hợp của hai dao động này có phương trình là x = 20 cos ( ω t + φ ) (cm). Giá trị cực đại của A 1 + A 2 gần giá trị nào nhất sau đây?
A. 25 cm
B. 20 cm
C. 40 cm
D. 35 cm
Đáp án D
Có A1 +A2 lớn nhất khi A1 = A2.
Có
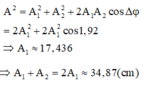
Đúng 0
Bình luận (0)
(Câu 40 Đề thi ĐH 2014 – Mã đề 319): Cho hai dao động điều hòa cùng phương với các phương trình lần lượt là
x
1
A
1
cos
(
ω
t
+
0
,
35
)
(
c
m
)
và
x
2
A...
Đọc tiếp
(Câu 40 Đề thi ĐH 2014 – Mã đề 319): Cho hai dao động điều hòa cùng phương với các phương trình lần lượt là x 1 = A 1 cos ( ω t + 0 , 35 ) ( c m ) và x 2 = A 2 . cos ( ω t - 1 , 57 ) ( c m ) . Dao động tổng hợp của hai dao động này có phương trình là x = 20 cos ( ω t + φ ) ( c m ) . Giá trị cực đại của (A1 + A2) gần giá trị nào nhất sau đây?
A. 25 cm
B. 20 cm
C. 40 cm
D. 35 cm
Đáp án D
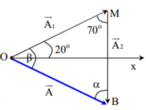
Áp dụng định lý hàm số sin ta có:
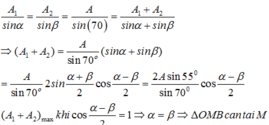
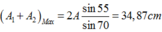
Đúng 0
Bình luận (0)
Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là
x
1
A
1
cos
(
ω
t
+
π
3
)
cm và
x
2
A
2
cos
(
ω
t...
Đọc tiếp
Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là x 1 = A 1 cos ( ω t + π 3 ) cm và x 2 = A 2 cos ( ω t - π 6 ) cm. Biên độ dao động của vật là :
A. A 1 2 + A 2 2 .
B. |A1 - A2|
C. A1 + A2
D. A 1 + A 2 2
Biên độ tổng hợp của hai dao động vuông pha
A = A 1 2 + A 2 2
Đáp án A
Đúng 0
Bình luận (0)
Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là
x
1
A
1
cos
(
ωt
+
π
3
)
cm và
x
2
A
2
cos
(
ωt
-
π...
Đọc tiếp
Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là x 1 = A 1 cos ( ωt + π 3 ) cm và x 2 = A 2 cos ( ωt - π 6 ) cm. Biên độ dao động của vật là :
![]()
![]()
![]()
![]()
Cho
x
2
A
1
cos
(
ω
t
+
π
3
)
c
m
,
x
2
A
2
cos
(
ω
t
-
π
40
)
c
m
là hai phương trình của hai dao động điều...
Đọc tiếp
Cho x 2 = A 1 cos ( ω t + π 3 ) c m , x 2 = A 2 cos ( ω t - π 40 ) c m là hai phương trình của hai dao động điều hòa cùng phương.Biết phương trình dao động tổng hợp là x = 5 cos ( ω t + φ ) cm. Để tổng biên độ của các dao động thành phần (A1 + A2) cực đại thì φ có giá trị là:
A. π / 6
B. π / 24
C. 5 π / 12
D. π / 12
- Với x = x1 + x2:
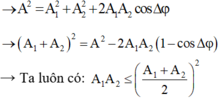
⇒ Tích A1A2 nhỏ nhất khi A1 = A2 khi đó tổng A1 + A2 là lớn nhất → Các vectơ hợp thành tam giác cân:
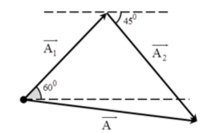
- Từ hình vẽ ta có:
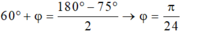
Đúng 0
Bình luận (0)
Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là x1A1cos(ωt + π/3) cm và x2 A2cos(ωt - π/6) cm. Biên độ dao động của vật là :
Đọc tiếp
Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là x1=A1cos(ωt + π/3) cm và x2 = A2cos(ωt - π/6) cm. Biên độ dao động của vật là :
![]()
![]()
![]()
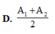
Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là
x
1
A
1
cos(ωt + π/3) cm và
x
2
A
2
cos(ωt - π/6) cm. Biên độ dao động của vật là: A.
A
1
2...
Đọc tiếp
Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là x 1 = A 1 cos(ωt + π/3) cm và x 2 = A 2 cos(ωt - π/6) cm. Biên độ dao động của vật là:
A. A 1 2 + A 2 2
B. A 1 - A 2
C. A 1 + A 2
D. A 1 + A 2 2
Đáp án A
Biên độ tổng hợp của hai dao động vuông pha A = A 1 2 + A 2 2
Đúng 0
Bình luận (0)
Hai dao động điều hòa thành phần cùng phương, có phương trình
x
1
A
1
cos
(
ω
t
+
π
3
)
c
m
,
x
2
A
2
cos
(
ω
t
-...
Đọc tiếp
Hai dao động điều hòa thành phần cùng phương, có phương trình x 1 = A 1 cos ( ω t + π 3 ) c m , x 2 = A 2 cos ( ω t - π 4 ) c m . Biết phương trình dao động tổng hợp là x = 5 cos ( ω t + φ ) c m . Để ( A1 +A2) có giá trị cực đại thì φ có giá trị là
A. π 12
B. 5 π 12
C. π 24
D. π 6
Áp dụng công thức Freshnel về tổng hợp dao động ta có:
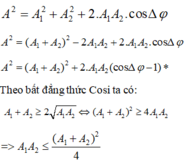
Thay vào biểu thức *, chú ý rằng biểu thức
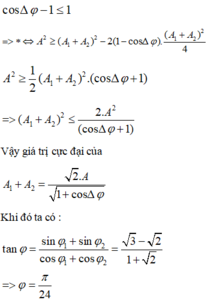
Đáp án C
Đúng 0
Bình luận (0)
Cho
x
1
A
1
cos
(
ωt
+
π
3
)
và
x
2
A
2
cos
(
ωt
-...
Đọc tiếp
Cho x 1 = A 1 cos ( ωt + π 3 ) và x 2 = A 2 cos ( ωt - π 4 ) là hai phương trình của hai dao động điều hòa cùng phương. Biết phương trình dao động tổng hợp là x = 5 cos ( ωt + φ ) . Để tổng biên độ của các dao động thành phần (A1 + A2) cực đại thì φ có giá trị là
A. π 6
B. π 24
C. 5 π 12
D. π 12
Đáp án B
![]()
![]()
![]()
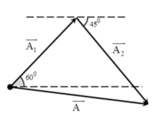
→ Ta luôn có
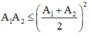
→ Tích A1 A2 nhỏ nhất khi (A1 = A2) khi đó tổng (A1 + A2) là lớn nhất
→ Các vectơ hợp thành tam giác cân.
+ Từ hình vẽ ta có:
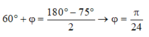
Đúng 0
Bình luận (0)
Cho hai dao động điều hòa cùng phương với các phương trình li độ lần lượt là
x
1
A
1
c
o
s
(
ω
t
+
π
/
9
)
c
m
và
x
2
A
2
c
o
s
(
ω
t
-
π
/
2
)
c
m
. Dao động tổn...
Đọc tiếp
Cho hai dao động điều hòa cùng phương với các phương trình li độ lần lượt là x 1 = A 1 c o s ( ω t + π / 9 ) c m và x 2 = A 2 c o s ( ω t - π / 2 ) c m . Dao động tổng hợp của hai dao động này có biên độ 20 cm. Đặt A = A 1 + A 2 thì giá trị lớn nhất của A gần nhất với giá trị
A. 25 cm
B. 30 cm
C. 35 cm
D. 40 cm
Chọn đáp án C
A t 2 = A 1 2 + A 2 2 + 2 A 1 A 2 cos φ ⇔ 20 2 = A 1 2 + A 2 2 + 2 A 1 A 2 cos 11 18 π
⇒ 20 2 = A 1 + A 2 2 − 2 , 68. A 1 A 2 ≥ A 1 + A 2 2 − 2 , 68. A 1 + A 2 2 4 = 0 , 33 A 1 + A 2 2
⇒ A 1 + A 2 ≤ 34 , 9 c m .
Đúng 0
Bình luận (0)