Ta có :

\(x^3-3x^2-3x+1=0\)

\(\Leftrightarrow x^3+x^2-4x^2-4x+x+1=0\)

\(\Leftrightarrow x^2\left(x+1\right)-4x\left(x+1\right)+\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^2-4x+1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x^2-4x+1=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=-1\\\left(x-2\right)^2-3=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=-1\\x=2\pm\sqrt{3}\end{cases}}\)

Vậy tập nghiệm của phương trình là : \(S=\left\{-1;2+\sqrt{3};2-\sqrt{3}\right\}\)

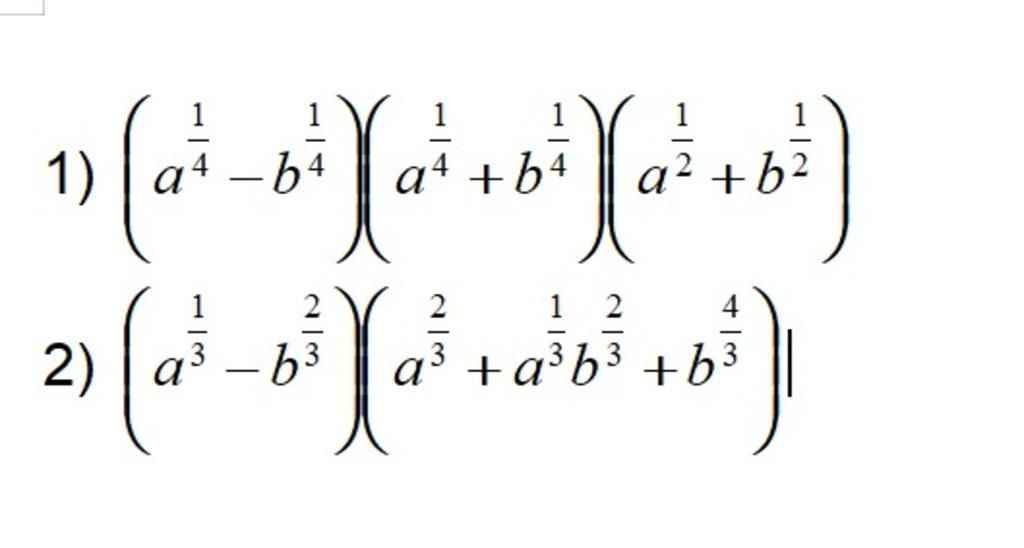
`1)(a^[1/4]-b^[1/4])(a^[1/4]+b^[1/4])(a^[1/2]+b^[1/2])`

`=[(a^[1/4])^2-(b^[1/4])^2](a^[1/2]+b^[1/2])`

`=(a^[1/2]-b^[1/2])(a^[1/2]+b^[1/2])`

`=a-b`

`2)(a^[1/3]-b^[2/3])(a^[2/3]+a^[1/3]b^[2/3]+b^[4/3])`

`=(a^[1/3]-b^[2/3])[(a^[1/3])^2+a^[1/3]b^[2/3]+(b^[2/3])^2]`

`=(a^[1/3])^3-(b^[2/3])^3`

`=a-b^2`

bài 2 :

0,25x³+x²+x=0

<=>0,25x³+0,5x²+0,5x²+x=0

<=>0,25x²(x+2)+0,5x(x+2)=0

<=>(x+2)(0,25x²+0,5x)=0

<=>(x+2)x(0,25x+0,5)=0

<=>x+2=0 hoặc x=0 hoặc 0,25x+0,5=0

=>x=-2 hoặc x=0 hoặc x=-2

vậy x=0 hoặc x=-2

2) 9x²+ 12x+ 4

<=>(3x)²+ 2.3x.2+ 2² <=>(3x+ 2)²

3) 4x⁴+ 20x²+ 25

<=>(2x²)²+ 2.2x².5+ 5² <=>(2x²+5)²

4) 25x²- 20xy+ 4y²

<=> (5x)²- 2.5x.2y+ (2y)²<=> (5x-2y)²

5) 9x⁴- 12x²y+ 4y²

<=> (3x²)²- 2.3x².2.y+ (2y)²<=> (3x²- 2y)²

6) 4x⁴- 16x²y³+ 16y⁶

<=> (2x²)²- 2.2x².4y³+ (4y³)²<=> (2x²- 4y³)²

7) 9x⁴- 12x⁵+ 4x⁶

<=> (3x²)²- 2.3x².2x³+ (2x³)²<=> (3x²- 2x³)²

a) \(=\left(x-2\right)^2\)

b) \(=\left(3x-2\right)^2\)

c) \(=\left(x-3y\right)^2\)

d) \(=\left(\dfrac{x}{2}+1\right)^2\)

e) \(=\left(x-4\right)^2\)

f) \(=\left(\dfrac{1}{2}xy^2+1\right)^2\)

g) \(=\left(x-1\right)\left(x+1\right)\)

h) \(=\left(5x-4\right)\left(5x+4\right)\)

a) x²-4x+4=\(\left(X-2\right)^2\)

b)9x²-12x+4=\(\left(3x-2\right)^2\)

c)x²-6xy+9y^{2=\(\left(x-3y\right)^2\)}

d)x²/4+x+1=\(\left(\dfrac{x}{2}+1\right)^2\)

e)-8x+16+x² =\(X^2-8x+16=\left(x-4\right)^2\)

f)xy²+1/4x²y⁴+1 => sai đề

g)x²-1=\(\left(X-1\right)\left(x+1\right)\)

h)25x²-16=\(\left(5x-4\right)\left(5x+4\right)\)

x^2 -3^2=0

(x+3).(x-3)=0

x+3=0 hoặc x-3=0

x=-3 hoặc x=3

        \(x^2-9=0\)

⇔ \(x^2-3^2=0\)

⇔ \(\left(x-3\right)\left(x+3\right)=0\)

⇒  \(\left[{}\begin{matrix}x-3=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)

Vậy \(x=\pm3\)

Đặt \(A=x-x^2-1\)\(\Rightarrow2A=2x-2x^2-2=-\left(x^2-2x+1\right)-x^2-1=-\left[\left(x-1\right)^2+x^2\right]-1< 0\)

\(\Rightarrow2A< 0\Rightarrow A< 0\)