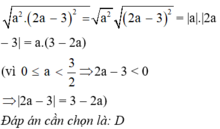\((a2+2a+3)(a2−2a+3)\)

Những câu hỏi liên quan
Rút gọn biểu thức sau:
a)(a2 + 2a + 3)(a2 + 2a -3)
b)(x - y + 6)(x + y - 6)
Mọi người trình bày cách giải giúp mình với nha,mình cảm ơn!
a,hđt số 3 = \(\left(a^2+2a\right)^2-9\)
b,hđt số 3=\(\left[x-\left(y-6\right)\right]\left[x+\left(y-6\right)\right]\)(đổi dấu làm ngoặc khi trước nó là dấu trừ)=\(x^2-\left(y-6\right)^2\)
Đúng 2
Bình luận (0)
a) \(\left(a^2+2a+3\right)\left(a^2+2a-3\right)\)
\(=\left(a^2+2a\right)^2+3.\left(-3\right)\)
\(=\left(a^2+2a\right)^2-9\)
b) \(\left(x-y+6\right)\left(x+y-6\right)\)
\(=\left[x-\left(y-6\right)\right]\left[x+\left(y-6\right)\right]\)
\(=x^2-\left(y-6\right)^2\)
Đúng 3
Bình luận (0)
Cho đa thức
A(x)=12x3+2ax+a2
B(x)=2x2-|2a+3|x+a2
Tìm a biết A(1)=B(-2)
Ta có \(A\left(1\right)=B\left(-2\right)\Leftrightarrow12+2a+a^2=8-\left|2a+3\right|\left(-2\right)+a^2\)
\(\Leftrightarrow4+2a=2\left|2a+3\right|\)
đk a >= -2
\(\left[{}\begin{matrix}4a+6=4+2a\\4a+6=-2a-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=-1\left(tm\right)\\a=-\dfrac{5}{3}\left(ktm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của:
N=a2+b2+2a-b-\(\dfrac{1}{4}\)
P=a2+2a-4ab+5b2-2b-10
a) Ta có: \(N=a^2+b^2+2a-b-\dfrac{1}{4}\)
\(=a^2+2a+1+b^2-b+\dfrac{1}{4}-\dfrac{3}{2}\)
\(=\left(a+1\right)^2+\left(b-\dfrac{1}{2}\right)^2-\dfrac{3}{2}\ge-\dfrac{3}{2}\forall a,b\)
Dấu '=' xảy ra khi a=-1 và \(b=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của:
N=a2+b2+2a-b\(-\dfrac{1}{4}\)
P=a2+2a-4ab+5b2-2b-10
a) Ta có: \(N=a^2+b^2+2a-b-\dfrac{1}{4}\)
\(=a^2+2a+1+b^2-b+\dfrac{1}{4}-\dfrac{3}{2}\)
\(=\left(a+1\right)^2+\left(b-\dfrac{1}{2}\right)^2-\dfrac{3}{2}\ge-\dfrac{3}{2}\forall a,b\)
Dấu '=' xảy ra khi a=-1 và \(b=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức (a+b/b-2b/b-a).b-a/a2+b2+(a2+1/2a-1-a/2):a+2/1-2a
Phân tích thành nhân tử :
a). a(b2 + c2 + bc) + b(c2 + a2 + ac) + c(a2 + b2 + ab);
b). (a + b + c) (ab + bc + ca) - abc
c*). a(a + 2b)3 - b(2a + b)3.
c: Ta có: \(a\left(a+2b\right)^3-b\left(2a+b\right)^3\)
\(=a^4+6a^3b+12a^2b^2+8ab^3-8a^3b-12a^2b^2-6ab^3-b^4\)
\(=a^4-2a^3b+2ab^3-b^4\)
\(=\left(a-b\right)\left(a+b\right)\left(a^2+b^2\right)-2ab\left(a^2-b^2\right)\)
\(=\left(a-b\right)^3\cdot\left(a+b\right)\)
Đúng 1
Bình luận (0)
Rút gọn biểu thức
a
2
(
2
a
-
3
)
2
với
0
≤
a
3
2
ta được: A. a (2a – 3) B.
(
3
–
2
a
)
a
2
C....
Đọc tiếp
Rút gọn biểu thức a 2 ( 2 a - 3 ) 2 với 0 ≤ a < 3 2 ta được:
A. a (2a – 3)
B. ( 3 – 2 a ) a 2
C. ( 2 a – 3 ) a 2
D. (3 – 2a) a
Rút gọn phân thức
a
2
−
2a
−
8
a
2
+
2a
ta được? A.
a
2
+
a
B.
a
−
4...
Đọc tiếp
Rút gọn phân thức a 2 − 2a − 8 a 2 + 2a ta được?
A. a 2 + a
B. a − 4 2 + a
C. -8
D. a − 4 a
Câu 87*: Biến đổi ab sqrt{dfrac{a}{3b}} - a2sqrt{dfrac{3b}{a}} msqrt{3ab}với a 0 , b 0 thì m bằng: A . dfrac{-2a}{3}; B . dfrac{2a}{3}; C.dfrac{-2}{3}; D.3a.giải hộ mik vs
Đọc tiếp
Câu 87*: Biến đổi ab \(\sqrt{\dfrac{a}{3b}}\) - a2\(\sqrt{\dfrac{3b}{a}}\)= m\(\sqrt{3ab}\)với a > 0 , b > 0 thì m bằng:
A . \(\dfrac{-2a}{3}\); B . \(\dfrac{2a}{3}\); C.\(\dfrac{-2}{3}\); D.3a.
giải hộ mik vs
\(ab\cdot\sqrt{\dfrac{a}{3b}}-a^2\sqrt{\dfrac{3b}{a}}\)
\(=a\sqrt{ab}-a^2\cdot\dfrac{\sqrt{3b}}{\sqrt{a}}\)
\(=a\sqrt{ab}-a\sqrt{a}\cdot\sqrt{3b}\)
\(=a\sqrt{ab}\left(1-\sqrt{3}\right)\)
\(\Leftrightarrow m=\dfrac{a\sqrt{ab}\left(1-\sqrt{3}\right)}{\sqrt{3ab}}=\dfrac{a\left(\sqrt{3}-3\right)}{3}\)
Đúng 0
Bình luận (0)