Cho tam giác ABC. BC=40CM, AH=45CM. Độ dài phân giác AD= 45CM. Tính AB, AC.

Những câu hỏi liên quan
tam giác ABC có BC= 40cm, đường phân giác AD dài 45cm, đường cao AH dài 36cm. Tính độ dài BD, DC
ABCEHD
+) Kẻ AE là phân giác ngoài của góc BAC
Mà AD là phân giác của góc BAC nên AD vuông góc với AE => tam giác EAD vuông tại A
+) Áp dụng ĐL Pi - ta go trong tam giác vuông AHD có: DH = √AD2−AH2=√452−362=27 cm
+) Áp dụng hệ thức lượng trong tam giác vuông EAD có: AD2 = DH. DE => DE = AD2 / DH = 452/ 27 = 75 cm
+)Áp dụng tính chất tia phân giác trong và ngoài tam giác có: BDDC =ABAC =EBEC
Đặt BD = x (0 < x < 40) => CD = 40 - x. Ta có:
x40−x =75−x75+(40−x) (do EB = DE - BD; EC = DE + DC)
=> x. (115 - x) = (40 - x).(75 - x)
<=> 115x - x2 = 3000 - 115x + x2 <=> x2 - 115x + 1500 = 0
=> x = 100 (Loại) hoặc x = 15 (thoả mãn)
Vậy BD = 15 cm hoặc BD = 40 - 15 = 25 cm (Nếu ta đổi vị trí B và C cho nhau)
Cho tam giác ABC có AB= 30cm, AC=45cm,BC=50cm.Vẽ phân giác AD.
a) Tính DB,DC,đường cao AH
b) Qua D vẽ đường thẳng song song với AB cắt AC tại E,qua D vẽ đường thẳng song song với AC cắt AB tại F.Tứ giác AEDF là hình gì ,tính độ dài các cạnh tứ giác AEDF.
Cho tam giác ABC vuông tại A vẽ đường cao AH chia cạnh huyền BC thành hai đoạn thẳng BH20cm và CH45cm a)Chứng minh tam giác HBA đồng dạng với tam giác HAC b)Tính độ dài AHc)Tính diện tích tam giác ABC d)Cho AB10 căn 3 ,AC15 căn 3 .Gọi AD là đường phân giác trong của góc A và AH là đường cao .Tính tỉ số diện tích của tam giác ABC và tam giác ACD
Đọc tiếp
Cho tam giác ABC vuông tại A vẽ đường cao AH chia cạnh huyền BC thành hai đoạn thẳng BH=20cm và CH=45cm
a)Chứng minh tam giác HBA đồng dạng với tam giác HAC
b)Tính độ dài AH
c)Tính diện tích tam giác ABC
d)Cho AB=10 căn 3 ,AC=15 căn 3 .Gọi AD là đường phân giác trong của góc A và AH là đường cao .Tính tỉ số diện tích của tam giác ABC và tam giác ACD
Cho tam giác ABC đồng dạng với tam giác A'B'C'. Cho biết AB = 6cm, BC = 10cm, AC = 14cm và chu vi tam giác A'B'C' bằng 45cm. Hãy tính độ dài các cạnh của tam giác A'B'C'
Ta có:
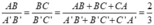
Từ đó tính được A'B' = 9cm, B'C' = 15cm, A'C' = 21cm
Đúng 0
Bình luận (0)
1/cho tam giác ABC có BC=27cm AB=36cm AC=45cm
a/cm tam giác ABC vuông
b/kẻ ah vuông góc với bc tính AH BH CH
tự vẽ hình nhé =))
a/Ta có BC2 =729; AB2 =1296; AC2 = 2025
=> BC2 + AB2 =AC2
=>729+1296=2025 ( định lý Py ta go trog tam giác )
=> vậy tam giác ABC vuông tại C
Đúng 0
Bình luận (0)
Xét tam giác ABC có:
\(AC^2=45^2=2025\)
\(AB^2+BC^2=36^2+27^2=2025\)
\(\Rightarrow AC^2=AB^2+BC^2\left(=2025\right)\)
\(\Rightarrow\)Tam giác ABC vuông tại B (Định lí Py-ta-go đảo)
Đúng 0
Bình luận (0)
Tam giác ABC có AB =30cm, AC=45cm, BC=50cm, đường phân giác BD. Tính độ dài BD
(giải = chương trình lớp 8, k sử dụng cos, sin)
BÀI 1: Tam giác ABC vuông tại A, ĐƯỜNG PHÂN GIÁC bd. Tính AB,AC biết rằng AD4cm, DC5 cmBài 2: Tam giác ABC có AB30cm, AC45cm, BC50cm, đương phân giác BDa)Tính BD, BCb)Qua D vẽ DE//AB,DF//AC, E và F thuộc AC và AB. Tính các cạnh của tứ giác AEDFBìa 3: Tam giác ABC vuông tại A, AB 36cm, AC 48cm, đường phân giác AK. Tia phân giác của góc B cắt AK tại I. Qua I kẻ đường thẳng song song với BC cắt AB ở D, cắt AC ở E.a)Tính độ dài BKb)Tính tỉ số AI/AKc) Tính độ dài DE
Đọc tiếp
BÀI 1: Tam giác ABC vuông tại A, ĐƯỜNG PHÂN GIÁC bd. Tính AB,AC biết rằng AD=4cm, DC=5 cm
Bài 2: Tam giác ABC có AB=30cm, AC=45cm, BC=50cm, đương phân giác BD
a)Tính BD, BC
b)Qua D vẽ DE//AB,DF//AC, E và F thuộc AC và AB. Tính các cạnh của tứ giác AEDF
Bìa 3: Tam giác ABC vuông tại A, AB =36cm, AC= 48cm, đường phân giác AK. Tia phân giác của góc B cắt AK tại I. Qua I kẻ đường thẳng song song với BC cắt AB ở D, cắt AC ở E.
a)Tính độ dài BK
b)Tính tỉ số AI/AK
c) Tính độ dài DE
Cho tam giác ABC có các đường phân giác BD và CE( \(D\in AC,E\in AB\)). Biết \(\frac{AD}{DC}=\frac{2}{3};\frac{AE}{EB}=\frac{5}{6}\), chu vi tam giác ABC là 45cm. Tính độ dài các cạnh của tam giác ABC.
Áp dụng định lý đường phân giác trong tam giác, ta được:
\(\frac{AB}{AD}=\frac{BC}{DC}\Rightarrow\frac{AB}{BC}=\frac{AD}{DC}=\frac{2}{3}\Rightarrow\frac{AB}{2}=\frac{BC}{3}\)(1)
Lại ap dụng định lý đường phân giác trong tam giác, ta được:
\(\frac{AC}{AE}=\frac{BC}{EB}\Rightarrow\frac{AC}{BC}=\frac{AE}{EB}=\frac{5}{6}\Rightarrow\frac{AC}{5}=\frac{BC}{6}\)(2)
Từ (1) và (2) suy ra \(\frac{AB}{4}=\frac{AC}{5}=\frac{BC}{6}=\frac{45}{15}=3\)
Vậy độ dài các cạnh của tam giác ABC lần lượt là 12;15;18 (cm)
Hình bạn tự vẽ nhé
Xét tam giác ABC có CE là đường phân giác của góc ACB (gt)
\(\Rightarrow\frac{AE}{EB}=\frac{AC}{BC}\)( tính chất đường phân giác trong của tam giác )
\(\Rightarrow\frac{AC}{BC}=\frac{5}{6}\)( Vì\(\frac{AE}{EB}=\frac{5}{6}\))
\(\Rightarrow6AC=5BC\)
Xét tam giác ABC có đường phân giác BD của góc ABC(gt)
\(\Rightarrow\frac{AD}{DC}=\frac{AB}{BC}\)( tích chất của đường phân giác trong của tam giác )
\(\Rightarrow\frac{AB}{BC}=\frac{2}{3}\)( Vì \(\frac{AD}{DC}=\frac{2}{3}\))
\(\Rightarrow3AB=2BC\)
Theo bài ra ta có: \(\hept{\begin{cases}6AC=5BC\\3AB=2BC\end{cases}}\)và \(AB+BC+CA=45\)
\(\Rightarrow\hept{\begin{cases}\frac{AC}{5}=\frac{BC}{6}\\\frac{AB}{4}=\frac{BC}{6}\end{cases}}\)
\(\Rightarrow\frac{AB}{4}=\frac{AC}{5}=\frac{BC}{6}=\frac{AB+AC+BC}{4+5+6}=\frac{45}{15}=3\)
\(\Rightarrow\hept{\begin{cases}AB=3.4=12\left(cm\right)\\AC=3.5=15\left(cm\right)\\BC=3.6=18\left(cm\right)\end{cases}}\)
Vậy ...
+) Xét tam giác ABC có : CE là đường phân giác ( GT )
\(\Rightarrow\frac{AE}{EB}=\frac{AC}{BC}=\frac{5}{6}\)( T/c đường phân giác trong tam giác )
\(\Rightarrow5BC=6AC\)
Tương tự xét tam giác ABC có BD là phân giác ( GT )
\(\Rightarrow\frac{AD}{DC}=\frac{AB}{BC}=\frac{2}{3}\)
\(\Rightarrow2BC=3AB\)
Ta có :
\(\hept{\begin{cases}5BC=6AC\\2BC=3AB\end{cases}}\)(1) và \(AB+AC+BC=45\)( Do diện tích tam giác ABC = 45cm )
Từ ( 1 )
\(\Rightarrow\hept{\begin{cases}\frac{BC}{6}=\frac{AC}{5}\\\frac{BC}{3}=\frac{AB}{2}\end{cases}\Rightarrow\hept{\begin{cases}\frac{BC}{6}=\frac{AC}{5}\\\frac{BC}{6}=\frac{AB}{4}\end{cases}\Leftrightarrow}}\frac{BC}{6}=\frac{AC}{5}=\frac{AB}{4}\)
Áp dụng TC của dãy tỉ số bằng nhau , ta có :
\(\frac{BC}{6}=\frac{AC}{5}=\frac{AB}{4}=\frac{BC+AC+AB}{6+5+4}=\frac{45}{15}=3\)
\(\Rightarrow\hept{\begin{cases}BC=18\\AC=15\\AB=12\end{cases}}\)
P/s : Bạn Châu sai chỗ nào zậy ?? k sai bừa !!
Xem thêm câu trả lời
Bài 1: Cho tam giác vuông ABC, vuông góc tại A. Chu vi tam giác là 75cm, Cạnh BC là 45cm. Hỏi:a) Tổng độ dài của cạnh AB và AC là bao nhiêu?b) Tính diện tích tam giác vuông ABC, biết cạnh AB hơn cạnh AC là 4cm. Bài 2: Cho tam giác ABC có chu vi 67cm, cạnh AB và AC có tổng độ dài 47 cm.a) Tính độ dài BC.b) Tính diện tích tam giác ABC, biết chiều cao AH là 15cm. Bài 3: Một tam giác vuông có cạnh góc vuông thứ nhất là 24cm, cạnh góc vuông thứ hai bằng 5/8 cạnh góc vuông thứ nhất. Tính di...
Đọc tiếp
Bài 1: Cho tam giác vuông ABC, vuông góc tại A. Chu vi tam giác là 75cm, Cạnh BC là 45cm. Hỏi:
a) Tổng độ dài của cạnh AB và AC là bao nhiêu?
b) Tính diện tích tam giác vuông ABC, biết cạnh AB hơn cạnh AC là 4cm.
Bài 2: Cho tam giác ABC có chu vi 67cm, cạnh AB và AC có tổng độ dài 47 cm.
a) Tính độ dài BC.
b) Tính diện tích tam giác ABC, biết chiều cao AH là 15cm.
Bài 3: Một tam giác vuông có cạnh góc vuông thứ nhất là 24cm, cạnh góc vuông thứ hai bằng 5/8 cạnh góc vuông thứ nhất. Tính diện tích tam giác vuông đó.
Bài 4: Cho tam giác vuông ABC, vuông góc tại A. Chu vi tam giác là 90cm, Cạnh BC là 45cm. Hỏi:
a) Tổng độ dài của cạnh AB và AC là bao nhiêu?
b)Tính diện tích tam giác vuông ABC, biết cạnh AC bằng 4/5 cạnh AB.
Bài 1:
a: AB+AC=75-45=30(cm)
b: AB=(30+4):2=17(cm)
=>AC=13cm
\(S=17\cdot13=221\left(cm^2\right)\)
Bài 2:
a: BC=67-47=20(cm)
b: \(S=\dfrac{15\cdot20}{2}=15\cdot10=150\left(cm^2\right)\)
Đúng 0
Bình luận (1)






















