Cho góc xOy với tia phân giác Ot. Lấy điểm M trên tia Ot, kẻ MK vuông góc với Ox tại K và MH vuông góc với Oy tại H. Chứng minh Ot là trung trực đoạn KH

Những câu hỏi liên quan
c) MN là đường trung trực của đoạn thẳng BC. Bài 4: Cho góc xOy nhọn, vẽ tia Ot là tia phân giác của góc xOy. Trên tia Ot lấy điểm M tùy ý. Từ M kẻ đường thẳng vuông góc với tia Ox cắt tia Ox tại A, cắt tia Oy tại D. Từ M kẻ đường thẳng vuông góc với tia Oy, cắt tia Oy tại B, cắt tia Ox tại C. Chứng minh : a) OAM OBM b) AC BD c) OM AB d) AB // CD Bài 5: Cho tam giác ABC (AC AB), tia phân giác của góc BAC cắt BC tại D. Trên cạnh AC lấy E sao cho AE AB. a) Chứng minh BD DE. b) Kéo dài...
Đọc tiếp
c) MN là đường trung trực của đoạn thẳng BC. Bài 4: Cho góc xOy nhọn, vẽ tia Ot là tia phân giác của góc xOy. Trên tia Ot lấy điểm M tùy ý. Từ M kẻ đường thẳng vuông góc với tia Ox cắt tia Ox tại A, cắt tia Oy tại D. Từ M kẻ đường thẳng vuông góc với tia Oy, cắt tia Oy tại B, cắt tia Ox tại C. Chứng minh : a) OAM OBM b) AC = BD c) OM AB d) AB // CD Bài 5: Cho tam giác ABC (AC > AB), tia phân giác của góc BAC cắt BC tại D. Trên cạnh AC lấy E sao cho AE = AB. a) Chứng minh BD = DE. b) Kéo dài AB và DE cắt nhau tại K. Chứng minh AKD ACD . c) Chứng minh ΔKBE = ΔCEB. d) Tìm điều kiện của tam giác ABC để DE vuông góc với AC.
Bài 5:
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE
Đúng 0
Bình luận (0)
Cho góc nhọn xOy có Ot là tia phân giác. Trên tia Ot lấy điểm M,kẻ MA vuông góc Chứng minh: tam giác OMA=tam giác OMB Chứng minh Om là đường trung trực của đoạn ab Gọi H,k lần lượt là giao điểm của AM với tia Oy và BM với tia Ox chứng minh ab // hk
Xét ΔOMA vuông tại M và ΔOMB vuông tại M có
OA=OB
OM chung
Do đó: ΔOMA=ΔOMB
Đúng 0
Bình luận (0)
Cho xOy=90 độ, Ot là tia phân giác xOy. Từ m thuộc Ot vẽ MH vuông góc với Ox tại H, MK vuông góc với Oy tại K. Lấy E nằm giữa O và H, lấy F nằm trên tia đối của tia KO có HE=KF. Tính EMH?
Cho góc nhọn xOy và Ot là tia phân giác của góc xOy. Trên tia Ot lấy điểm M, kẻ MA vuông góc với Ox tại A, MB vuông góc với Oy tại B
a) Xét tam giác vuông AMO và tam giác vuông BMO :
góc MOA = góc MOB (gt)
OM là cạnh chung
=>tam giác vuông AMO = tam giác vuông BMO (cạnh huyền + góc nhọn)
=> OA=OB ( 2 cạnh tương ứng)
b) theo a) ta có : tam giác AMO = tam giác BMO
=>góc AMO = góc BMO
=> MO là tia phân giác của góc AMB
c) gọi C là giao điểm của OM và AB
Xét tam giác OAC và tam giác OBC có:
góc AOC = góc BOC (gt)
OC là cạnh chung
OA = OB (theo a)
=>tam giác OAC = tam giác OBC
=> góc ACO = góc BCO
mà hai góc này kề bù
=> góc ACO = góc BCO = 90 độ
=> OM vuông góc với AB
Đúng 2
Bình luận (3)
Cho góc nhọn xOy và Ot là tia phân giác của góc xOy. Trên tia Ot lấy điểm M, kẻ MA vuông góc với Ox tại A, MB vuông góc với Oy tại B
cho góc xOy là góc nhọn .Kẻ tia phân giác Ot của góc xOy. lấy điểm A thuộc thía Ox , điểm B thuộc thìa Oy sao cho OAOB. Qua A kẻ đường thẳng vuông góc với Ox cắt Ot tại C.a)chứng minh tam giác OACtam giác OBCb)chứng minh CB vuông góc với Oy và OC là đường trung trực của đoạn thẳng ABc)kéo dài đường thẳng BC cắt tia Ox tại D. so sánh BC và CDd)Qua B kẻ đường thẳng cuông góc với Ox tại I và cắt Ốt tại H . kẻ HK vuông góc với Oy
Đọc tiếp
cho góc xOy là góc nhọn .Kẻ tia phân giác Ot của góc xOy. lấy điểm A thuộc thía Ox , điểm B thuộc thìa Oy sao cho OA=OB. Qua A kẻ đường thẳng vuông góc với Ox cắt Ot tại C.
a)chứng minh tam giác OAC=tam giác OBC
b)chứng minh CB vuông góc với Oy và OC là đường trung trực của đoạn thẳng AB
c)kéo dài đường thẳng BC cắt tia Ox tại D. so sánh BC và CD
d)Qua B kẻ đường thẳng cuông góc với Ox tại I và cắt Ốt tại H . kẻ HK vuông góc với Oy
Cho góc nhọn xOy. Lấy M là một điểm nằm trên tia phân giác Ot của góc xOy. Kẻ MQvuông góc với Ox(Qthuộc Ox); Mh vuông góc với Oy(H thuộc Oy)
a) Chứng minh MQ=MH
b) Nối QH cắt Ot ở G. Chứng minh GQ=GH
c) Chứng minh QH vuông góc với OM
Kí hiệu tam giác là t/g
a) Xét t/g QOM vuông tại Q và t/g HOM vuông tại H có:
OM là cạnh chung
QOM = HOM ( vì OM là p/g của HOQ)
Do đó, t/g QOM = t/g HOM ( cạnh huyền và góc nhọn kề)
=> MQ = MH (2 cạnh tương ứng) (đpcm)
b) t/g QOM = t/g HOM (câu a)
=> QMO = HMO (2 góc tương ứng)
Xét t/g QMG và t/g HMG có:
MG là cạnh chung
QMG = HMG (cmt)
MQ = HM (câu a)
Do đó, t/g QMG = t/g HMG (c.g.c)
=> QG = HG (2 cạnh tương ứng) (đpcm)
c) t/g QMG = t/g HMG (câu b)
=> QGM = HGM (2 góc tương ứng)
Mà QGM + HGM = 180o
Nên QGM = HGM = 90o
=> QH _|_ OM (đpcm)
Đúng 0
Bình luận (9)
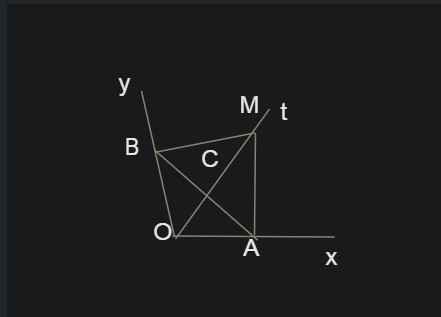
Cho góc xOy = 400 có Ot là tia phân giác. Trên Ot lấy điểm M, qua M kẻ đường vuông góc với Ot cắt Ox tại A và cắt Oy tại B. Trên tia Mt lấy điểm N sao cho MN =MO
a) Chứng minh: tam giác OMA = tam giác OMB.
b) Chứng minh: BN =BO.
c) Chứng minh: BN // OA; OAB = NBA.
d) Tính các góc của tam giác OBN.
Bài 1. Cho góc xOy nhọn. Kẻ tia phân giác Ot của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA OB. Từ A kẻ đường thẳng vuông góc với tia Ox và cắt tia Ot tại C.a) Chứng minh tam giác AOC tam giác BOC.b) Chứng minh CB I Oy.c) Chứng minh OC là đường trung trực của đoạn thẳng AB.d) Kẻ BI | Ox tại I, BI cắt OC tại H. Kẻ HK I Oy tại K. Chứng minh 3 điểm A, H, K thẳng hàng.e) Giả sử góc xOy 60° và OH 3m. Tính khoảng cách từ điểm H tới hai cạnh Ox và Oy.
Đọc tiếp
Bài 1. Cho góc xOy nhọn. Kẻ tia phân giác Ot của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Từ A kẻ đường thẳng vuông góc với tia Ox và cắt tia Ot tại C.
a) Chứng minh tam giác AOC = tam giác BOC.
b) Chứng minh CB I Oy.
c) Chứng minh OC là đường trung trực của đoạn thẳng AB.
d) Kẻ BI | Ox tại I, BI cắt OC tại H. Kẻ HK I Oy tại K. Chứng minh 3 điểm A, H, K thẳng hàng.
e) Giả sử góc xOy = 60° và OH = 3m. Tính khoảng cách từ điểm H tới hai cạnh Ox và Oy.
a: Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
=>ΔOAC=ΔOBC
b: ΔOAC=ΔOBC
=>góc OBC=90 độ
=>CB vuông góc Oy
c: OA=OB
CA=CB
=>OC là trung trực của AB
Đúng 0
Bình luận (0)
cho góc nhọn xOy. Lấy M là một điểm nằm trên tia phân giác OT của góc xOy. Kẻ MQ vuông góc với Ox ( Q thuộc Ox), MH vuông góc với Oy( H thuọc Oy)
a, Chứng Minh MQ=MH
b, Nối QH cắt Ot ở G. Chứng Minh GQ=GH
c, Chứng Minh GH=OM





















