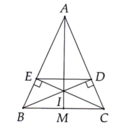
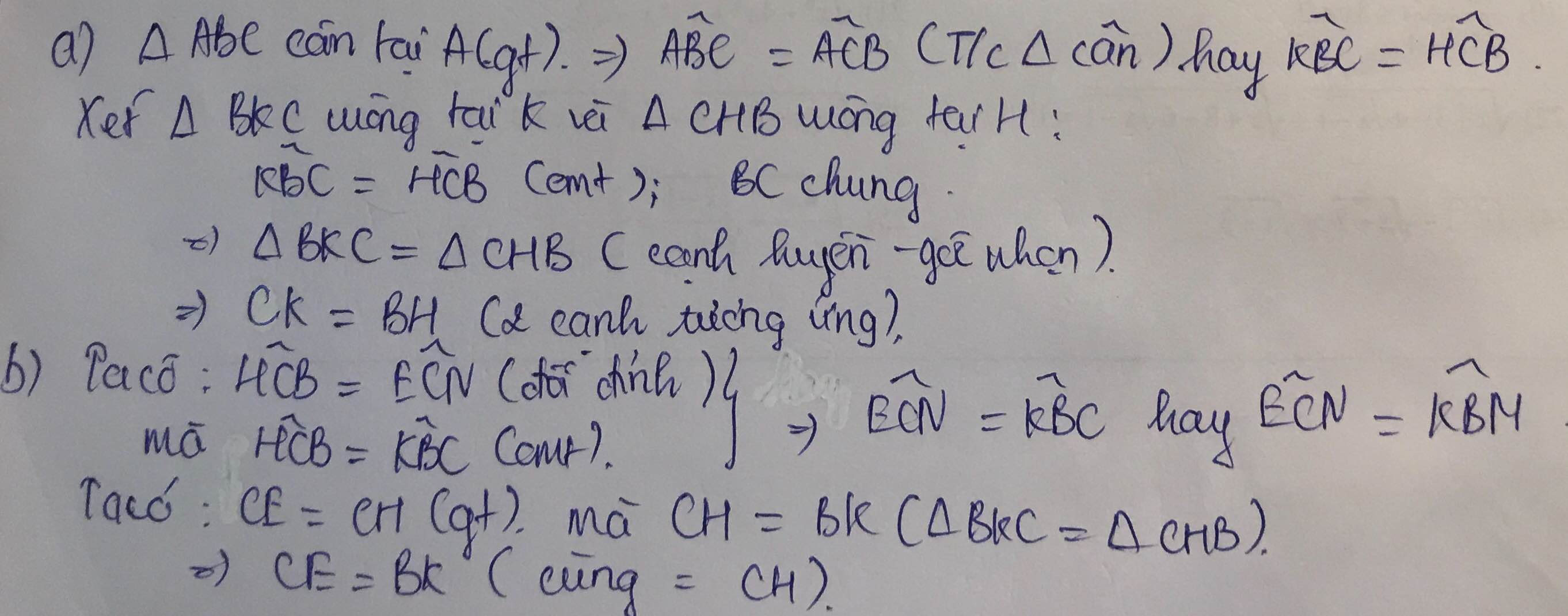Cho tam giác ABC cân tại A có Â < \(90^o\).Qua B kẻ BH vuông góc với AC (HϵAC). Qua C kẻ CE vuông góc với AB(EϵAB).Gọi M là giao điểm của BH và CE.
a) Chứng minh rằng:BE=CH
b) Chứng minh rằng:tam giác BEM = tam giác CHM
c) Chứng minh rằng:EH song song BC
d) Gọi giao điểm của AM và BC là D . CHứng minh rằng:AD vuông góc BC