Hãy chia tứ giác ABCD thành 8 tam giác cân không có miền chung.

Những câu hỏi liên quan
Cho tứ giác ABCD,hai đường chéo của tứ giác chia tứ giác làm bốn hình tam giác không có điểm cong chung,biết số đo diện tích của tam giác đều là số nguyên.Chứng minh : Tích 4 số này là số chính phương
Trong tứ giác ABCD lấy 4 điểm MNPQ sao cho 8 điểm không có 3 điểm nào thẳng hàng. Nối các điểm bới các đoạn thẳng:
a) Có bao nhiêu tứ giác không có điểm chung?
b) Có bao nhiêu tam giác không có điểm chung?
Trong tứ giác ABCD lấy 4 điểm MNPQ sao cho 8 điểm không có 3 điểm nào thẳng hàng. Nối các điểm bới các đoạn thẳng:
a) Có bao nhiêu tứ giác không có điểm chung?
b) Có bao nhiêu tam giác không có điểm chung?
Đường chéo \(AC\) chia tứ giác \(ABCD\) thành hai tam giác \(ACB\) và \(ACD\) (Hình 7). Tính tổng các góc của tam giác \(ACB\) và tam giác \(ACD\). Từ đó, ta có nhận xét gì về tổng các góc của tứ giác \(ABCD\) .

Xét \(\Delta ABC\) ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} = 180^\circ \) (tính chất tổng ba góc trong tam giác)
Xét \(\Delta DAC\) ta có:
\(\widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ \)
Ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} + \widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ + 180^\circ \)
\(\widehat B + \widehat D + \left( {\widehat {BAC} + \widehat {DAC}} \right) + \left( {\widehat {BCA} + \widehat {DCA}} \right) = 360^\circ \)
\(\widehat B + \widehat D + \widehat {BAD} + \widehat {BCD} = 360^\circ \)
Vậy tổng các góc của tứ giác \(ABCD\) bằng \(360^\circ \)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Hãy chia tứ giác đã cho thành 3 phần có diện tích bằng nhau.
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD ⁓ ΔBDC. Chọn câu sai. A.
A
B
B
D
A
D
B
C
B. ABCD là hình thang C.
B
D
2
A
B
.
D
C...
Đọc tiếp
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD ⁓ ΔBDC. Chọn câu sai.
A. A B B D = A D B C
B. ABCD là hình thang
C. B D 2 = A B . D C
D. AD // BC
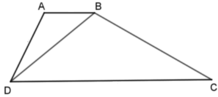
Vì ΔABD ⁓ ΔBDC (gt) nên A B D ^ = B D C ^ (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AB // CD suy ra ABCD là hình thang (dấu hiệu nhận biết) hay B đúng
Lại có ΔABD ⁓ ΔBDC nên A B B D = A D B C (cạnh tương ứng) nên A đúng
ΔABD ⁓ ΔBDC => A B B D = B D D C (cạnh tương ứng)
=> AB.CD = B D 2 hay C đúng
Chỉ có D sai
Đáp án: D
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD ⁓ ΔBDC. Cho AB = 2cm, AD = 3cm, CD = 8cm. Tính đọ dài cạnh còn lại của tứ giác ABCD.
A. BC = 6cm
B. BC = 4cm
C. BC = 5cm
D. BC = 3cm
Vì ΔABD ⁓ ΔBDC nên A B B D = B D D C = A D B C , tức là 2 B D = B D 8 = 3 B C
Ta có B D 2 = 2.8 = 16 nên BD = 4 cm
Suy ra BC = 8.3 4 = 6 cm
Vậy BD = 4cm, BC = 6cm
Đáp án: A
Đúng 0
Bình luận (0)
Cho hình thang ABCD(AB//CD) đường chéo BD chia hình thang thành 2 tam giác cân. Tam giác ABD cân tại A. Tam giác BCD cân tại B. Tính các góc của hình thang cân đó.Cho hình thang ABCD(AB//CD) đường chéo BD chia hình thang thành 2 tam giác cân. Tam giác ABD cân tại A. Tam giác BCD cân tại B. Tính các góc của hình thang cân đó.
Cho hình thang ABCD(AB//CD) đường chéo BD chia hình thang thành 2 tam giác cân. Tam giác ABD cân tại A. Tam giác BCD cân tại B. Tính các góc của hình thang cân đó.Cho hình thang ABCD(AB//CD) đường chéo BD chia hình thang thành 2 tam giác cân. Tam giác ABD cân tại A. Tam giác BCD cân tại B. Tính các góc của hình thang cân đó.
Trong hình thang cân ABCD (AB//CD) đặt m là sđ góc D (m<180 độ ) thì:D=C=m và A=B=180 độ-m
Tam giác ABD cân tại A =>^ABD=^ADB
AB//CD tạo với cát tuyến BD 2 góc so le trong ^ABD=^CDB
Suy ra ^ADB=^CDB,lại có tia DB nằm giữa 2 tia DA và DC nên tia DB là tia phân giác ^ADC=m độ
Vậy ^ABD= (1/2).m
Tam giác BCD cân tại D =>^DBC=^DCB=m độ
Tia BD nằm giữa 2 tia BA,BC nên ^ABC=^ABD+^DBC=(1/2).m+m (độ)
=(3/2).m (độ)
Mà ^ABC=180-m (độ),nên (3/2).m(độ)=180-m(độ)
hay 5/2.m=180 độ => m=360độ:5=72 độ
và 180 độ-m=108 độ
Trả lời : Trong hình thang cân ABCD kể trên,sđ 2 góc nhọn C và D là 72 độ,sđ 2 góc còn lại là 108 độ
Đúng 1
Bình luận (0)












