lý thuyết về ngữ âm

Những câu hỏi liên quan
Hôm nay, cô sẽ giới thiệu với các em về Đường cong lãng quên Ebbinghaus- đây là một lý thuyết về việc quên được phát triển bởi nhà tâm lý học người Đức Hermann Ebbinghaus vào cuối thế kỷ XIX. Theo lý thuyết này, chúng ta có xu hướng quên đi các thông tin mà chúng ta đã học trước đó theo một đường cong đặc biệt.Theo Ebbinghaus, chúng ta quên đi khoảng 50% thông tin đã học trong vòng 20 phút đầu tiên và khoảng 70% thông tin đã học trong vòng một ngày. Tuy nhiên, nếu ta lặp lại việc học các thông t...
Đọc tiếp
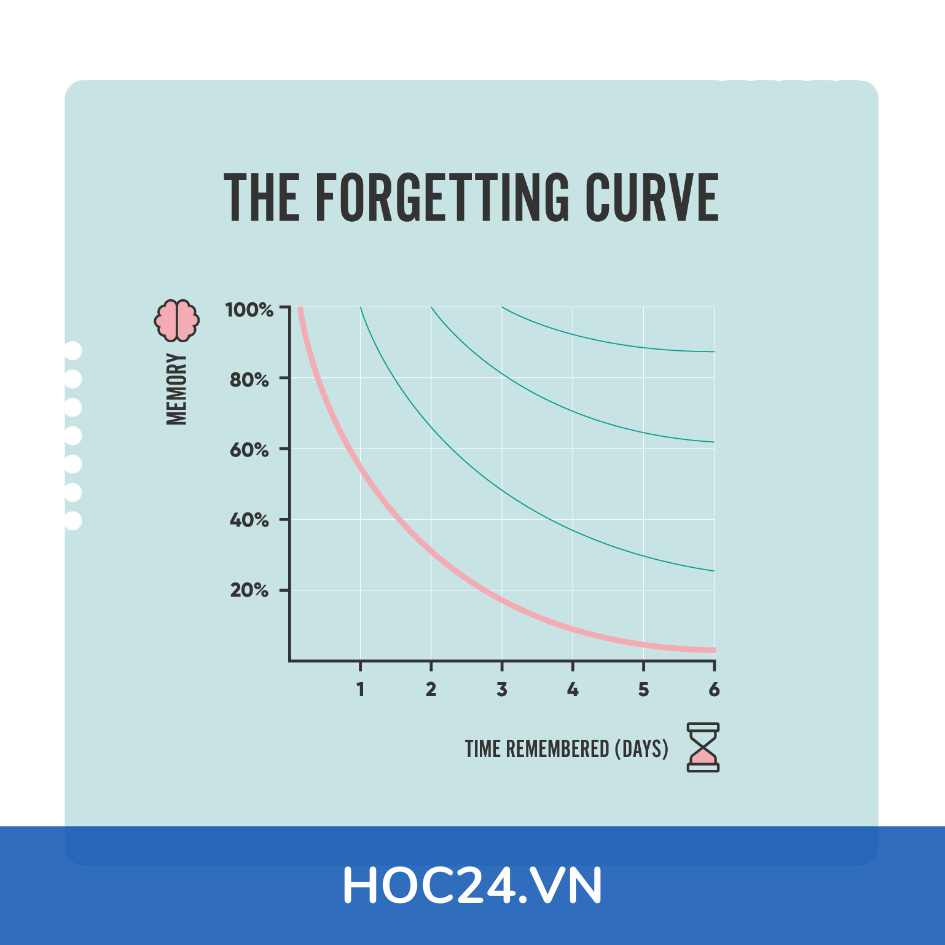
Hôm nay, cô sẽ giới thiệu với các em về "Đường cong lãng quên Ebbinghaus"- đây là một lý thuyết về việc quên được phát triển bởi nhà tâm lý học người Đức Hermann Ebbinghaus vào cuối thế kỷ XIX. Theo lý thuyết này, chúng ta có xu hướng quên đi các thông tin mà chúng ta đã học trước đó theo một đường cong đặc biệt.
Theo Ebbinghaus, chúng ta quên đi khoảng 50% thông tin đã học trong vòng 20 phút đầu tiên và khoảng 70% thông tin đã học trong vòng một ngày. Tuy nhiên, nếu ta lặp lại việc học các thông tin này trong khoảng thời gian khác nhau, chúng ta có thể giữ lại thông tin lâu hơn.
Sử dụng các kỹ thuật học tập hiệu quả và lặp lại các thông tin cần học sẽ giúp chúng ta giữ lại thông tin trong bộ nhớ lâu hơn và tránh bị lãng quên. Bạn nào có phương pháp ghi nhớ kiến thức nào hay và đã áp dụng thành công hãy chia sẻ với các bạn nhé.
Chúc các em tuần mới học tập tốt và nhiều niềm vui <3
Các tips ghi nhớ kiến thức mà mình hay áp dụng:
+ Ghi các kiến thức cần thiết vào giấy note, giấy ghi chú
+ Highlight hoặc gạch chân vào những kiến thức cần thiết
+ Hãy dành thời gian khoảng 15-30 phút để xem lại những kiến thức cần học
+ Lập một thời gian biểu rõ ràng, thời gian học các môn học
Ở trên là mấy tips chung chung còn mấy môn như Toán, Lý, Hóa thì:
+ Hãy lấy một cuốn sổ hoặc một quyển vở ghi lại những công thức (ví dụ Hóa thì ghi công thức tính số mol, Toán thì ghi 7 hằng đẳng thức đáng nhớ v.v...) và nếu được thì mỗi môn 1 quyển để đỡ rối nhé
Còn mấy môn học lý thuyết thì:
+ Highlight, gạch chân dưới những ý chính
+ Đọc to và viết ra giấy để dễ nhớ kiến thức hơn (cái này mình hay áp dụng trong kì thi)
+ Mấy môn lý thuyết thì mình nghĩ học ở những chỗ yên ắng, thoải mái sẽ dễ vào hơn á
Chúc các bạn thành công <3
Đúng 13
Bình luận (11)
Em nghĩ các bạn cũng có thể mua một quyển note A5/A6 rồi ghi chú những kiến thức cần nhớ/chưa nhớ, mấy cái quyển đấy cũng có thể mang bên người để khi nào sắp thi thì cũng ôn được ạ...
Đúng 11
Bình luận (0)
Lý thuyết về đơn thức
1. Đơn thức
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến
2. Đơn thức thu gọn
Đơn thức thu gọn là đơn thức chỉ gồm một tích của một số với các biến, mà mỗi biến đã được nâng lên lũy thừa với số mũ nguyên dương (mỗi biến chỉ được viết một lần). Số nói trên gọi là hệ số (viết phía trước đơn thức) phần còn lại gọi là phần biến của đơn thức (viết phía sau hệ số, các biến thường viết theo thứ tự của bảng chữ cái).
Các bước thu gọn một đơn thức
Bước 1. Xác định dấu duy nhất thay thế cho các dấu có trong đơn thức. Dấu duy nhất là dấu "+" nếu đơn thức không chứa dấu "-" nào hay chứa một số chẵn lần dấu "-". Dấu duy nhất là dấu "-" trong trường hợp ngược lại.
Bước 2. Nhóm các thừa số là số hay là các hằng số và nhân chúng với nhau.
Bước 3. Nhóm các biến, xếp chúng theo thứ tự các chữ cái và dùng kí hiệu lũy thừa để viết tích các chữ cái giống nhau.
3. Bậc của đơn thức thu gọn
Bậc của đơn thức có hệ số khác không là tổng số mũ của tất cả các biến có trong đơn thức đó.Số thực khác 0 là đơn thức bậc không. Số 0 được coi là đơn thức không có bậc.4. Nhân đơn thức
Để nhân hai đơn thức, ta nhân các hệ số với nhau và nhân các phần biến với nhau.
Đúng 0
Bình luận (0)
Lấy VD về lệch chuẩn ngữ âm giữa các vùng miền ( Bắc, Trung, Nam)
( về các từ ngữ giữa các vùng miền phát âm khác nhau)
Thạch Sanh đã có nững hành động nào để chống lại âm mưu của mẹ con Lý thông
ngữ văn 6
Lên h mà hỏi nhé bạn !!!!
Đảm bảo sẽ có người trả lời !!!!!
Đúng ko mấy bạn ? hihi
Đúng 0
Bình luận (0)
Lý thuyết về cộng, trừ đa thức
1. Cộng đa thức
Muốn cộng hai đa thức ta có thể lần lượt thực hiện các bước:
- Viết liên tiếp các hạng tử của hai đa thức đó cùng với dấu của chúng.
- Thu gọn các hạng tử đồng dạng (nếu có).
2. Trừ đa thức
Muốn trừ hai đa thức ta có thể lần lượt thực iện các bước:
- Viết các hạng tử của đa thức thứ nhất cùng với dấu của chúng.
- Viết tiếp các hạng tử của đa thức thứ hai với dấu ngược lại.
- Thu gọn các hạng tử đồng dạng (nếu có).
Đúng 0
Bình luận (0)
1. Cộng đa thức
Muốn cộng hai đa thức ta có thể lần lượt thực hiện các bước:
- Viết liên tiếp các hạng tử của hai đa thức đó cùng với dấu của chúng.
- Thu gọn các hạng tử đồng dạng (nếu có).
2. Trừ đa thức
Muốn trừ hai đa thức ta có thể lần lượt thực iện các bước:
- Viết các hạng tử của đa thức thứ nhất cùng với dấu của chúng.
- Viết tiếp các hạng tử của đa thức thứ hai với dấu ngược lại.
- Thu gọn các hạng tử đồng dạng (nếu có).
Đúng 0
Bình luận (0)
1. Cộng đa thức
Muốn cộng hai đa thức ta có thể lần lượt thực hiện các bước:
- Viết liên tiếp các hạng tử của hai đa thức đó cùng với dấu của chúng.
- Thu gọn các hạng tử đồng dạng (nếu có).
2. Trừ đa thức
Muốn trừ hai đa thức ta có thể lần lượt thực iện các bước:
- Viết các hạng tử của đa thức thứ nhất cùng với dấu của chúng.
- Viết tiếp các hạng tử của đa thức thứ hai với dấu ngược lại.
- Thu gọn các hạng tử đồng dạng (nếu có).
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Lý thuyết về đơn thức đồng dạng.
1. Đơn thức đồng dạng
Định nghĩa: Hai đơn thức đồng dạng là hai đơn thức có hệ số khác không và có cùng phần biến.
Chú ý: Mọi số khác 0 được coi là đơn thức đồng dạng với nhau.
2. Cộng, trừ đơn thức đồng dạng
Quy tắc: Để cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến.
Đúng 0
Bình luận (0)
Tóm tắt lý thuyết
1. Đơn thức đồng dạng
Định nghĩa: Hai đơn thức đồng dạng là hai đơn thức có hệ số khác không và có cùng phần biến.
Chú ý: Mọi số khác 0 được coi là đơn thức đồng dạng với nhau.
2. Cộng, trừ đơn thức đồng dạng
Quy tắc: Để cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến
Đúng 0
Bình luận (0)
Về lý thuyết, kết luận nào sau đây đúng ? A. Trong một loài, sự kết hợp giữa hai loại giao tử đực và cái đều có (n+1) NST luôn tạo ra con lai có bộ NST (2n+1+1) B. Trong một loài, sự kết hợp giữa giao tử đực có (n+2) NST với giao tử cái có (n) NST tạo ra con lai có bộ NST (2n+1+1) hoặc (2n+2) C. Trong một loài, sự kết hợp giữa giao tử đực có (n+2) NST với giao tử cái có (n) NST tạo ra con lai có bộ NST (2n+1+1) D. Trong một loài, sự kết hợp giữa giao tử đực và cái đều có (n+1) NST tạo ra...
Đọc tiếp
Về lý thuyết, kết luận nào sau đây đúng ?
A. Trong một loài, sự kết hợp giữa hai loại giao tử đực và cái đều có (n+1) NST luôn tạo ra con lai có bộ NST (2n+1+1)
B. Trong một loài, sự kết hợp giữa giao tử đực có (n+2) NST với giao tử cái có (n) NST tạo ra con lai có bộ NST (2n+1+1) hoặc (2n+2)
C. Trong một loài, sự kết hợp giữa giao tử đực có (n+2) NST với giao tử cái có (n) NST tạo ra con lai có bộ NST (2n+1+1)
D. Trong một loài, sự kết hợp giữa giao tử đực và cái đều có (n+1) NST tạo ra con lai có bộ NST (2n+1+1) hoặc (2n+2)
Trong một loài, sự kết hợp giữa giao tử đực và cái đều có (n+1) NST tạo ra con lai
+ Có bộ NST (2n+1+1) nếu đột biến giao tử ở hai cặp NST khác nhau
+ Có bộ NST (2n+2) nếu đột biến giao tử ở cùng một cặp NST
Đáp án D
Đúng 0
Bình luận (0)
Lý thuyết về đại lượng tỉ lệ thuận
1. Công thức.
Hai đại lượng tỷ lệ thuận x và y liên hệ với nhau bởi công thức y = kx, với k là một hằng số khác ), (y tỉ lệ thuận với x theo hệ số tỉ lệ k).
2. Tính chất.
- Tỉ số hai giá trị tương ứng của hai đại lượng tỉ lệ thuận luôn không đổi và bằng hệ số tỉ lệ.
\(\frac{y1}{x1}=\frac{y2}{x2}=\frac{y3}{x3}\)= ....= k
- TÍố hai hai giá trị bất kì của đại lượng này bằng tỉ số hai giá trị tương ứng của địa lượng kia.
\(\frac{y1}{y2}=\frac{x1}{x2}\); \(\frac{y1}{y3}=\frac{x1}{x3}\)
Đúng 0
Bình luận (0)
Hai đại lượng tỷ lệ thuận x và y liên hệ với nhau bởi công thức y = kx, với k là một hằng số khác 0 (y tỉ lệ thuận với x theo hệ số tỉ lệ k).
Đúng 0
Bình luận (0)
1. Công thức.
Hai đại lượng tỷ lệ thuận x và y liên hệ với nhau bởi công thức y = kx, với k là một hằng số khác ), (y tỉ lệ thuận với x theo hệ số tỉ lệ k).
2. Tính chất.
- Tỉ số hai giá trị tương ứng của hai đại lượng tỉ lệ thuận luôn không đổi và bằng hệ số tỉ lệ.
y1x1=y2x2=y3x3y1x1=y2x2=y3x3 = ....= k
- TÍố hai hai giá trị bất kì của đại lượng này bằng tỉ số hai giá trị tương ứng của địa lượng kia.
y1y2=x1x2;y1y3=x1x3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
câu 2 :từ "tráng sĩ" quan hệ về nghĩa hay quan hệ về âm thanh . nếu quan hệ về âm thanh thì là từ láy còn quan hệ về nghĩa là từ ghép câu 3 : muốn xác định được trạng ngữ , các em phải tách chủ ngữ , vị ngữ ra phần còn lại là trạng ngữ Mik đg thi các bn giải nhanh giúp mik ạ
Thuyết Minh về thể thơ tám chữ - ngữ văn 9 - Thuyết Minh
























