. Cho tam giác ABC cân tại A, trung tuyến AM (M thuộc BC)
. a) Chứng minh ΔABM = ΔACM
Những câu hỏi liên quan
cho tam giác ABC cân tại A, Mlaf trung điểm của BCa)chứng minh rằng ΔABMΔACM, từ đó chứng minh AM vuông góc BCb)Cho BC6cm, AM4cm. Hãy tính độ dài cạnh ACc) Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BDCE. Chứng minh ΔADE când)TỪ B và C kẻ BH và CK theo thứ tự vuông góc với AD và AE (HϵAD, KϵAE). Chứng minh rằng BHCKmình cần gấp ạ
Đọc tiếp
cho tam giác ABC cân tại A, Mlaf trung điểm của BC
a)chứng minh rằng ΔABM=ΔACM, từ đó chứng minh AM vuông góc BC
b)Cho BC=6cm, AM=4cm. Hãy tính độ dài cạnh AC
c) Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Chứng minh ΔADE cân
d)TỪ B và C kẻ BH và CK theo thứ tự vuông góc với AD và AE (HϵAD, KϵAE). Chứng minh rằng BH=CK
mình cần gấp ạ
Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC. Chứng minh: a. ΔABM = ΔACM b. AM là tia phân giác của góc BAC c. AM là đường trung trực của đoạn thẳng BC
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó:ΔABM=ΔACM
b: Ta có: ΔABM=ΔACM
nên \(\widehat{BAM}=\widehat{CAM}\)
hay AM là tia phân giác của \(\widehat{BAC}\)
c: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: MB=MC
nên M nằm trên đường trung trực của BC(2)
từ (1) và (2) suy ra AM là đường trung trực của BC
Đúng 1
Bình luận (1)
3.Cho tam giác ABC cân tại A, trung tuyến AM.Gọi E và F lần lượt là các giao điểm của các phân giác trong \(ΔABM\)và \(ΔACM\).CHứng minh EF//BC
Cho tam giác ABC cân tại A.
a. Kẻ đường trung tuyến AM (M thuộc BC).
b. Chứng minh rằng AM là đường phân giác xuất phát từ đỉnh A của tam giác ABC.
a: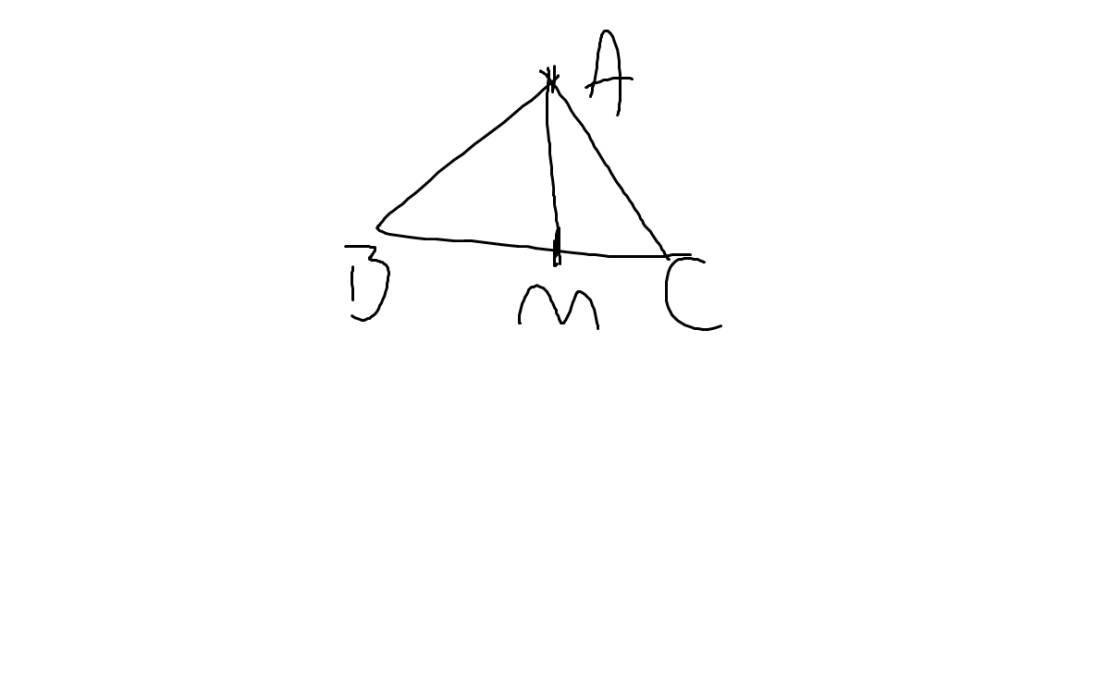 
b: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
Đúng 0
Bình luận (0)
Bài 8. Cho tam giác ABC có AB AC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BDCE. a) Chứng minh: ΔABM ΔACM. Từ đó suy ra AM ⊥ BC. b) Chứng minh ΔABD ΔACE. Từ đó suy ra AM là đường phân giác của góc DAE. c) Kẻ BK ⊥ AD (K∈AD). Trên tia đối của tia BK lấy điểm H sao cho BH AE, trên tia đối của tia AM lấy điểm N sao cho AN CE. Chứng minh MAD MBH và DN ⊥DH
Đọc tiếp
Bài 8. Cho tam giác ABC có AB = AC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE.
a) Chứng minh: ΔABM = ΔACM. Từ đó suy ra AM ⊥ BC.
b) Chứng minh ΔABD = ΔACE. Từ đó suy ra AM là đường phân giác của góc DAE.
c) Kẻ BK ⊥ AD (K∈AD). Trên tia đối của tia BK lấy điểm H sao cho BH = AE, trên
tia đối của tia AM lấy điểm N sao cho AN = CE. Chứng minh MAD = MBH và DN ⊥DH
Bài 1: Cho tam giác ABC cân tại A có các đường trung tuyến BE và CD . Chứng minh rằng BE bằng CD
Bài 2: Cho tam giác ABC có đường trung tuyến BE và CD, biết BE = CD . Chứng minh rằng tam giác ABC cân tại A
Bài 3: Cho tam giác ABC chứng minh rằng a) Nếu tam giác ABC vuông góc tại A , có trung tuyến AM =1/2 BC
b) Nếu trung tuyến AM =1/2 BC thì tam giác ABC vuông góc tại A
Bài 12: Cho tam giác ABC cân tại A, vẽ đường trung tuyến AM ( M thuộc BC ). Qua M kẻ đường thẳng song song với AB , cắt AC tại N . Gọi O là giao điểm của AM và BN . Chứng minh O là trọng tam của tam giác ABC.
Cho Tam giác ABC vuông cân tại A, trung tuyến AM. E thuộc BC, BH vuông góp với AE, CK vuông góc với AE.( H, K thuộc AE) . Chứng minh Tam giác MKH vuông cân .
cho tam giác abc vuông cân tại a , trung tuyến am . e thuộc bc , bh vuông góc với ae , ck vuông góc với ae , h và k thuộc ae . chứng minh tam giác mhk vuông cân
Cho tam giác ABC vuông cân tại A , trung tuyến AM , E thuộc BC ; BH vuông góc với AE ; CK vuông góc với AE.
Chứng minh tam giác MHK vuông cân .
Câu hỏi của Nguyễn Thị Vân - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại link bên trên nhé.
Đúng 0
Bình luận (0)
Viết một đoạn văn ngắn trong đó có sử dụng trạng ngữ, câu chủ động, câu bị động.
Đúng 0
Bình luận (0)