abcd*2=2014
Tìm abcd
Những câu hỏi liên quan
SABCD có ABCD là hình vuông cạnh bằng 2 , tam giác SAB đều , H là trung điểm AB
1, BC⊥ ( SAB)
2, SH ⊥ ( ABCD)
3, ((SBC);(ABCD))
4, ((SAD);(ABCD))
5,((SCD);(ABCD))
1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
2: ΔSAB đều
mà SH là trung tuyến
nên SH vuông góc AB
=>SH vuông góc (ABCD)
Đúng 1
Bình luận (0)
ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD
Đọc tiếp
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
bạn chia nhỏ đề ra đi ạ chứ bây giờ nhập đáp án xong kéo lên mệt lắm ạ
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD*ABCD
Đọc tiếp
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
*
A
B
C
D
Xem thêm câu trả lời
Tim so co 4 chu so abcd(abcd co gach tren dau )biet abcd=(5c+1)^2
Cho hình chiếu ABCD ABCD là hình vuông cạnh a căn 2 SC vuông góc ABCD SC = 2a
a, tam giác SAC, SAB vuông
b tính SA(ABCD) , SA(SCD) , SB(SCD)
Xem chi tiết
Xét tính đúng, sai của MĐ1.Nếu ABCD là hvuông thì ABCD là hbình hành2.Nếu ABCD là tam giác vuông thì ABC là tam giác có 1 góc bằng tổng 2 góc còn lại3.Nếu ABCD là tam giác có 1 góc bằng tổng 2 góc còn lại thì ABC là tam giác vuông4.ABCD là hvuông là đkiện cần và đủ để ABCD là hbình hành5.ABC là tam giác vuông là đkiện cần và đủ để ABC là tam giác có 1 góc tổng 2 góc còn lại6.ABCD là hcn là đkiện cần và đủ để ABCD là hvuông7.ABCD là hcn là đkiện cần để ABCD là hvuông
Đọc tiếp
Xét tính đúng, sai của MĐ
1.Nếu ABCD là hvuông thì ABCD là hbình hành
2.Nếu ABCD là tam giác vuông thì ABC là tam giác có 1 góc bằng tổng 2 góc còn lại
3.Nếu ABCD là tam giác có 1 góc bằng tổng 2 góc còn lại thì ABC là tam giác vuông
4.ABCD là hvuông là đkiện cần và đủ để ABCD là hbình hành
5.ABC là tam giác vuông là đkiện cần và đủ để ABC là tam giác có 1 góc = tổng 2 góc còn lại
6.ABCD là hcn là đkiện cần và đủ để ABCD là hvuông
7.ABCD là hcn là đkiện cần để ABCD là hvuông
1)Tứ giác ABCD có A+D=B+C.CM tứ giác ABCD là hình thang
2) Tứ giác ABCd có A=B;C=D.Cmr ABCD là hình thang cân
cho hình chóp S ABCD có đáy ABCD là hình chữ nhật. Biết AB= a căn 2; AD= a căn 3; SA vuông góc (ABCD), biết SC = a căn 7
a, tính góc giữa SB và (ABCD)
b. tính góc giữa SC và (SAD)
c, tính góc giữa (SBC) và (ABCD)
d, tính góc giữa (SBD) và (ABCD)
a: (SB;(ABCD))=(BS;BA)=góc SBA
AC=căn a^2+3a^2=2a
SA=căn SC^2-AC^2=a*căn 3
tan SBA=SA/AB=căn 3
=>góc SBA=60 độ
b: (SC;(SAD))=(SC;SD)=góc SCD
SD=căn SA^2+AD^2=2a*căn 3
cos SCD=(CS^2+CD^2-SD^2)/(2*CS*CD)=-2/căn 7
=>góc SCD=139 độ
Đúng 0
Bình luận (0)
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . Gọi chu vi tứ giác ABCD là PABCD Chứng minh
a)AC+BD>\(\dfrac{P_{ABCD}}{2}\)
b)Nếu AC<\(\dfrac{P_{ABCD}}{2}\) thì AC+BD<PABCD
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . gọi chu vi của tứ giác ABCD là PABCD . chứng minh
a) AC+BD>\(\dfrac{P_{ABCD}}{2}\)
b) Nếu AC<\(\dfrac{P_{ABCD}}{2}\) thì AC+BD<PABCD
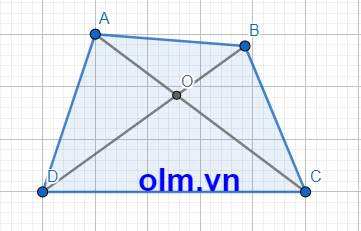
a, Xét \(\Delta\) AOB có: AO+OB > AB (trong tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Tương tự ta có: OC + OD > DC
OA + OD > AD
OB + OC > BC
Cộng vế với vế ta có:
OA+OB+OC+OD+OA+OD+OB+OC > AB +DC+AD+BC
(OA+OC)\(\times\)2 + (OB + OD)\(\times\)2 > PABCD
AC \(\times\) 2 + BD \(\times\) 2 > PABCD
AC + BD > \(\dfrac{P_{ABCD}}{2}\) (đpcm)
b, Xét \(\Delta\) ABD có: AB + AD > BD (trong tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại)
Tương tự ta có: AD + DC > AC
DC + CB > DB
CB + AB > AC
Cộng vế với vế ta có:
AB+AD+AD+DC+DC+CB+CB+AB >BD+ AC+DB+AC
2AB+2BC+2CD+2AD> 2AC + 2BD
2(AB + BC + CD + AD) > 2(AC + BD)
AB + BC + CD + AD > AC + BD
PABCD > AC + BD (đpcm)
Đúng 0
Bình luận (0)