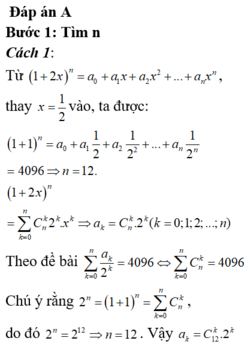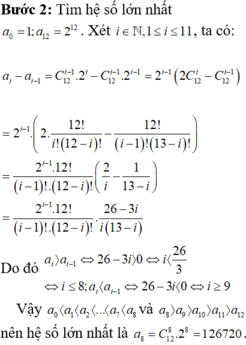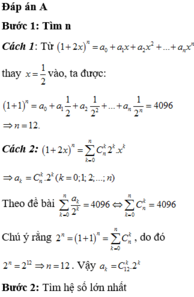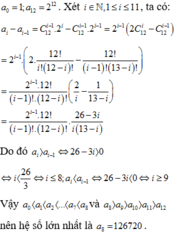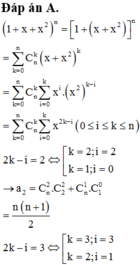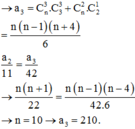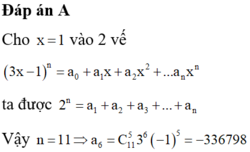cho f(x) = (2+x)1000 = ao + a1x + a2x2 + ....+ a1000x1000. Tìm hệ số lớn nhất trong khai triển

Những câu hỏi liên quan
Cho đa thức:
P
(
x
)
(
1
+
x
)
8
+
(
1
+
x
)
9
+
(
1
+
x
)
10
+
(
1
+...
Đọc tiếp
Cho đa thức: P ( x ) = ( 1 + x ) 8 + ( 1 + x ) 9 + ( 1 + x ) 10 + ( 1 + x ) 11 + ( 1 + x ) 12 . Khai triển và rú gọn ta được đa thức: P ( x ) = a o + a 1 x + a 2 x 2 + . . . + a 12 x 12 . Tìm hệ số a 8
A. 700
B. 715
C. 720
D. 730
Chọn B
Ta có a8= C88+C98+C108+C118+C128= 1+9+45+165+495= 715
Đúng 0
Bình luận (0)
Cho khai triển
1
+
2
x
n
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
n
x
n...
Đọc tiếp
Cho khai triển 1 + 2 x n = a 0 + a 1 x + a 2 x 2 + . . . + a n x n n ∈ ℕ * và các hệ số thỏa mãn a 0 + a 1 2 + . . . + a n 2 n = 4096 . Hệ số lớn nhất là
A. 126720
B. 1293600
C. 729
D. 924
Cho khai triển
(
1
+
2
x
)
n
a
0
+
a
1
x
+
a
2
x
2
+
…
+
a
n
x
n
(nÎN*) và các hệ số thỏa mãn
a
0
+...
Đọc tiếp
Cho khai triển ( 1 + 2 x ) n = a 0 + a 1 x + a 2 x 2 + … + a n x n (nÎN*) và các hệ số thỏa mãn a 0 + a 1 2 + . . . + a n 2 n = 4096 . Hệ số lớn nhất là
A. 126720
B. 1293600
C. 729
D. 924
Cho khai triển
1
+
x
+
x
2
n
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
2...
Đọc tiếp
Cho khai triển 1 + x + x 2 n = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n , biết a 2 11 = a 3 42 . Tìm số hạng chứa x 3 trong khai triển trên.
A. 210
B. 55
C. 615
D. 265
Cho khai triển
(
1
+
2
x
)
2019
a
0
+
a
1
x
+
a
2
x
2
+
.
.
....
Đọc tiếp
Cho khai triển ( 1 + 2 x ) 2019 = a 0 + a 1 x + a 2 x 2 + . . . . . + a n x n . Tính tổng các hệ số trong khai triển?
A. 2019
B. 3 2019
C. 3 2020
D. 2 2019
Chọn B
Ta có ![]()
![]()
Tổng các hệ số trong khai triển là: ![]()
Cho x = 1 ta có: ![]()
![]()
![]()
![]()
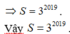
Đúng 0
Bình luận (0)
Biết tổng các hệ số trong khai triển
3
x
-
1
n
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
n
x
n
...
Đọc tiếp
Biết tổng các hệ số trong khai triển 3 x - 1 n = a 0 + a 1 x + a 2 x 2 + . . . + a n x n là 2 11 . Tìm a 6 .
A. a 6 = - 336798
B. a 6 = 336798
C. a 6 = - 112266
D. a 6 = 112266
Biết tổng các hệ số trong khai triển
3
x
−
1
n
a
0
+
a
1
x
+
a
2
x
2
+
...
a
n
x
n
là
2...
Đọc tiếp
Biết tổng các hệ số trong khai triển 3 x − 1 n = a 0 + a 1 x + a 2 x 2 + ... a n x n là 2 11 . Tìm a 6 .
A. a 6 = − 336798
B. a 6 = 336798
C. a 6 = − 112266
D. a 6 = 112266
Đáp án A
Cho x = 1 vào 2 vế 3 x − 1 n = a 0 + a 1 x + a 2 x 2 + ... a n x n ta được 2 n = a 1 + a 2 + a 3 + ... + a n
Vậy n = 11 ⇒ a 6 = C 11 5 3 6 − 1 5 = − 336798
Đúng 0
Bình luận (0)
Cho khai triển
P
x
1
+
2
x
12
a
0
+
a
1...
Đọc tiếp
Cho khai triển P x = 1 + 2 x 12 = a 0 + a 1 x + ... + a 12 x 12 . Tìm hệ số a k 0 ≤ k ≤ 12 lớn nhất trong khai triển trên.
A. C 12 8 2 8 .
B. C 12 9 2 9 .
C. C 12 10 2 10 .
D. 1 + C 12 8 2 8 .
Khai triển đa thức
1
3
+
2
3
x
10
thành đa thức
a
0
+
a
1
x
+
a
2
x
2
+
a
3...
Đọc tiếp
Khai triển đa thức 1 3 + 2 3 x 10 thành đa thức a 0 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4 + . . . + a 9 x 9 + a 10 x 10 a k ∈ ℝ , k = 0 , 1 , 2 , ... , 10
Tìm số lớn nhất trong các số a 0 , a 1 , a 2 , a 3 , ... , a 9 , a 10
A. a 8
B. a 7
C. a 5
D. a 6
Cho khai triển
1
+
x
+
x
2
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
2
n
x...
Đọc tiếp
Cho khai triển 1 + x + x 2 = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n với n ≥ 2 và a 0 , a 1 , a 2 , . . . , a 2 n là các hệ số. Tính tổng S = a 0 + a 1 + a 2 + . . . + a 2 n biết a 3 14 = a 4 41
A. S = 3 10
B. S = 3 12
C. S = 2 10
D. S = 2 12