Vẽ ΔMNP có Mˆ = 90∘
. Qua N kẻ tia Nt // MP (tia Nt thuộc nửa mặt phẳng bờ là đường
thẳng MN không chứa điểm P). Vẽ tia phân giác Px của NPM cắt MN tại I, cắt Nt tại H.
Vẽ MK ⊥ PI. Vẽ đường thẳng d là đường trung trực của đoạn thẳng HN.
Những câu hỏi liên quan
Bài 2. Vẽ hình theo yêu cầu sau:
- Vẽ có .
- Qua N kẻ tia Nt // MP (tia Nt thuộc nửa mặt phẳng bờ là đường thẳng MN không chứa điểm P).
- Vẽ tia phân giác Px của góc NPM cắt MN tại I, cắt Nt tại H.
- Vẽ
- Vẽ đường thẳng d là đường trung trực của đoạn thẳng HN
Bài 4. Cho hai đường thẳng AB và MN cắt nhau tại O sao cho 0 AOM < 90 . Trên nửa mặt phẳng bờ AB có chứa tia OM, vẽ tia OC sao cho tia OM là tia phân giác của góc AOC. Trên nửa mặt phẳng bờ AB có chứa tia ON vẽ tia OD sao cho tia ON là tia phân giác của góc BOD. Chứng tỏ rằng hai tia OC, OD là hai tia đối nhau.
Cho hai đường thẳng AB và MN cắt nhau tại O sao cho
A
O
M
^
90
°
. Trên nửa mặt phẳng bờ AB có chứa tia OM, vẽ tia OC sao cho tia OM là tia phân giác của góc AOC. Trên nửa mặt phẳng bờ AB có chứa tia ON vẽ tia OD sao cho tia ON là tia phân giác của góc BOD. Chứng tỏ rằng hai tia OC, OD là hai tia đối nhau
Đọc tiếp
Cho hai đường thẳng AB và MN cắt nhau tại O sao cho A O M ^ < 90 ° . Trên nửa mặt phẳng bờ AB có chứa tia OM, vẽ tia OC sao cho tia OM là tia phân giác của góc AOC. Trên nửa mặt phẳng bờ AB có chứa tia ON vẽ tia OD sao cho tia ON là tia phân giác của góc BOD. Chứng tỏ rằng hai tia OC, OD là hai tia đối nhau
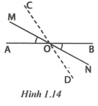
Theo đề bài ta có A O M ^ = M O C ^ , B O N ^ = D O N ^ mà A O M ^ = B O N ^ (hai góc đối đỉnh) nên M O C ^ = D O N ^ .
Ta có M O D ^ + D O N ^ = 180 ° (hai góc kề bù), suy ra M O D ^ + M O C ^ = 180 ° .
Hai góc MOD và MOC là hai góc kề, có tổng bằng 180 ° nên hai tia OC, OD đối nhau.
Chứng tỏ một tia là tia phân giác
Đúng 0
Bình luận (0)
Cho tam giác ABC, Ax là tia phân giác góc A. Qua C kẻ đường
thẳng song song Ax, cắt tia đối của tia AB tại D. Ay là tia phân giác của góc DAC. Trên nửa mặt phẳng bờ AD không chứa điểm C, vẽ tia Az sao cho góc zAD=góc ADC.
a) CMR: 𝐴𝐷𝐶 ̂ = 𝐴𝐶𝐷 ̂
Cho tam giác ABC, Ax là tia phân giác góc A. Qua C kẻ đường
thẳng song song Ax, cắt tia đối của tia AB tại D. Ay là tia phân giác của góc DAC. Trên nửa mặt phẳng bờ AD không chứa điểm C, vẽ tia Az sao cho góc zAD=góc ADC.
a) CMR: 𝐴𝐷𝐶 ̂ = 𝐴𝐶𝐷 ̂
a) Ta có:
CD//Ax(gt)CD//Ax(gt)
⇒ ˆACD=ˆCAxACD^=CAx^ (so le trong)
ˆBAx=ˆADCBAx^=ADC^ (đồng vị)
mà
Đúng 1
Bình luận (0)
a) Ta có:
CD//Ax(gt)CD//Ax(gt)
⇒ ˆACD=ˆCAxACD^=CAx^ (so le trong)
ˆBAx=ˆADCBAx^=ADC^ (đồng vị)
mà
Đúng 1
Bình luận (0)
a) Ta có:
CD//Ax(gt)CD//Ax(gt)
⇒ ˆACD=ˆCAxACD^=CAx^ (hai góc so le trong)
ˆBAx=ˆADCBAx^=ADC^ (hai góc đồng vị)
mà
Đúng 1
Bình luận (0)
Cho Tam Giác ABC có A ^{90^o}. Kẻ tia phân giác của ABC cắt AC tại M. Từ A kẻ đường thẳng song song với BM, cắt tia đối tia BC tại D.a, CM DABBDAb, Trên nửa mặt phẳng bờ AC khong chứa b, vẽ tia Ay sao cho CAyC. CM đường thẳng BM cắt đường thẳng chứa tia Ay.c, Trên nửa mặt phẳng bờ BC không chứa A, vẽ tia Bz sao cho ABz 90^o. CM CayCbz
Đọc tiếp
Cho Tam Giác ABC có A = \(^{90^o}\). Kẻ tia phân giác của ABC cắt AC tại M. Từ A kẻ đường thẳng song song với BM, cắt tia đối tia BC tại D.
a, CM DAB=BDA
b, Trên nửa mặt phẳng bờ AC khong chứa b, vẽ tia Ay sao cho CAy=C. CM đường thẳng BM cắt đường thẳng chứa tia Ay.
c, Trên nửa mặt phẳng bờ BC không chứa A, vẽ tia Bz sao cho ABz = \(90^o\). CM Cay=Cbz
cho tam giác ABC có góc A=90 . kẻ tia phân giác của ABC cắt AC tại M . từ A kẻ đường thẳng song song với BM , đường thẳng này cắt tia đối của BC tại D
a, chứng minh DAB =BDA
b, trên nửa mặt phẳng bờ AC ko chứa B vẽ tia Ay sao cho BCA =CAy. chứng minh đường thẳng MB cắt đường thẳng y
c, trên nửa mặt phẳng bờ BC ko chứa tia A vẽ tia Bz sao cho ABz=90. chứng minh CAy =CBz
Cho 4 điểmM, E, F, N lần lượt nằm trên đường thẳng a sao cho MF = NE. Gọi d là đường trung trực của MN, d cắt MN tại O.b/ Trên nửa mặt phẳng bờ chứa tia ON vẽ 2 tia Ox, Oy sao cho ON là tia phân giác của xÔy. Vẽ Oz là tia đốicủa tia Oy. CMR: Od là tia phân giác của xÔz.
Cho ΔABC có gó B50 đọ. Trên nửa mặt phẳng chứa bờ C có bở là đường thẳng AB, vẽ tia à sao cho goc BAx 130 độ. Tia phân giác của góc BAx cắt đường thẳng BC tại D. Trên nửa mặt phẳng không chứa Ccos bờ là đường thẳng AB vẽ tia By sao cho góc CByCDA. . Tia By cắt tia đốicủa tia à tại E. Tia phân giác của BAE cắt BE tại F. Qua B vẽ đường vuong góc với AD cắt Ax tại I. chứng minh rằng:a)góc ABEAEBb)Tổng số đo các góc của ΔABC180 độc) AF vuông góc với BEd) ABIAIB
Đọc tiếp
Cho ΔABC có gó B=50 đọ. Trên nửa mặt phẳng chứa bờ C có bở là đường thẳng AB, vẽ tia à sao cho goc BAx= 130 độ. Tia phân giác của góc BAx cắt đường thẳng BC tại D. Trên nửa mặt phẳng không chứa Ccos bờ là đường thẳng AB vẽ tia By sao cho góc CBy=CDA. . Tia By cắt tia đốicủa tia à tại E. Tia phân giác của BAE cắt BE tại F. Qua B vẽ đường vuong góc với AD cắt Ax tại I. chứng minh rằng:
a)góc ABE=AEB
b)Tổng số đo các góc của ΔABC=180 độ
c) AF vuông góc với BE
d) ABI=AIB