Cho hình thang ABCD có , hai đường chéo vuông góc với nhau tại H.
Biết . Khi đó độ dài HC là
Chỉ cần kết quả thôi

Những câu hỏi liên quan
Cho hình thang ABCD có B=C=90, hai đường chéo vuông góc với nhau tại H. BiếtAB=3CA5HA=3CM . Khi đó độ dài HC là cm.
Cho hình thang ABCD có , hai đường chéo vuông góc với nhau tại H.
Biết AB = 3căn 5 ,HA=3. Khi đó độ dài HC là cm.
Câu 5:
Cho hình thang ABCD có , hai đường chéo vuông góc với nhau tại H.
Biết . Khi đó độ dài HC là cm.
đề thiếu, phải ghi đủ thì mấy bạn mới làm được chứ
Đúng 0
Bình luận (0)
Cho hình thang ABCD có góc B=C=90 độ , hai đường chéo vuông góc với nhau tại H.
Biết AB=\(3\sqrt{5}\),\(HA=3\) . Khi đó độ dài HC là
hệ thức lượng \(AB^2=AH\cdot AC\)
TÌM ĐƯỢC AC=15cm
suy ra HC=AC-AH=15-3=12cm
Đúng 0
Bình luận (0)
Cho hình thang ABCD đấy là AB, CD.Hai đường chéo vuông góc với nhau tại H.Biết AC=16cm, BD=12cm.Tính chiều cao của hình thang.
Bài 3: Cho hình thang ABCD (đáy AB, CD) 𝐴̂ = 𝐷̂ = 900 có hai đường chéo vuông góc với nhau tại O, AB = 15cm, AD = 20cm.
a) Tính độ dài OB, OD
b) Tính độ dài AC
c) Tính diện tích hình thang ABCD
a: Xét ΔDAB vuông tại A có
\(DB^2=AB^2+AD^2\)
hay DB=25(cm)
Xét ΔDAB vuông tại A có AO là đường cao ứng với cạnh huyền DB
nên \(\left\{{}\begin{matrix}AD^2=DO\cdot DB\\AB^2=BO\cdot BD\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DO=16\left(cm\right)\\OB=9\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
\(a,BD=\sqrt{AB^2+AD^2}=25\left(cm\right)\left(pytago\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}AD^2=OD\cdot BD\\AB^2=OB\cdot BD\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}OD=\dfrac{AD^2}{BD}=16\left(cm\right)\\OB=\dfrac{AB^2}{BD}=9\left(cm\right)\end{matrix}\right.\)
\(b,\) Áp dụng HTL:
\(\left\{{}\begin{matrix}AO^2=DO\cdot OB=144\\AD^2=AO\cdot AC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AO=12\left(cm\right)\\AC=\dfrac{AD^2}{AO}=\dfrac{100}{3}\left(cm\right)\end{matrix}\right.\)
\(c,DC=\sqrt{AD^2+AC^2}=\dfrac{20\sqrt{34}}{3}\left(cm\right)\\ S_{ABCD}=\dfrac{1}{2}AD\left(AB+CD\right)=10\left(\dfrac{20\sqrt{34}}{3}+15\right)=\dfrac{450+200\sqrt{34}}{3}\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Cho hình thang cân ABCD có hai đường chéo vuông góc với nhau độ dài đường cao 3,(001) cm Tính diện tích của hình thag đó
Cho hình thang ABCD vuông tại A có cạnh đáy AB bằng 6cm, cạnh bên AD bằng 4cm và hai đường chéo vuông góc với nhau. Tính độ dài các cạnh DC, CB và đường chéo DB.
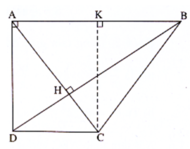
Hai đường chéo AC, BD cắt nhau tại H. Trong tam giác vuông ABD, ta có:
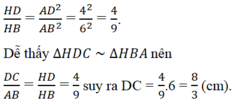
Kẻ đường cao CK của tam giác ABC, dễ thấy KB = AB – DC = 6 - 8/3 = 10/3.
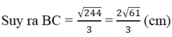
Tam giác vuông ABD có D B 2 = A B 2 + A D 2 = 6 2 + 4 2 = 52, từ đó DB = 52 = 2 13 (cm)
Đúng 0
Bình luận (0)
Hai đường chéo hình thang ABCD (AB//CD) vuông góc vs nhau tại O và có độ dài là 3,6 dm và 6 dm. Tính diện tích hình thang ABCD.
Diện tích tam giác ABD = 1/2 AO x BD
Diện tích tam giác BDC = 1/2 CO x BD
Cộng diện tích 2 tam giác này lại thì chính là diện tích hình thang ABCD = 1/2 BD x (AO+CO) = 1/2 BD x AC = 1/2x3,6 x 6 = 10.8 dm2
Đúng 0
Bình luận (0)


















