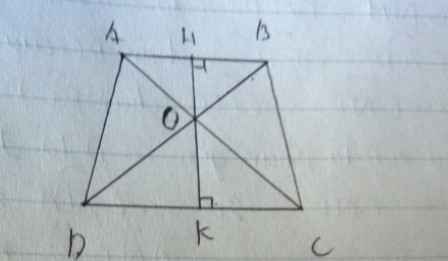
CHO hình thang ABCD có 2 đáy AB và CD ( đáy CD dài gấp 2 lần đáy nhỏ AB )
a) hãy so sánh diện tích của 2 hình tam giác ABC và BCD ?
b) hãy chứng tỏ diện tích của hai hình tam giác AOD = diện tích hình tam giác BOC?
a:bang nhau
b:bang nhau vi no co cung chieu cao ,do dai day va neu cat ra thi AOD vua khit voi BOC
Cho hình thang ABCD có đáy nhỏ AB ,hai đường chéo AC và BD của hình thang cắt nhau tại O .So sánh diện tích tam giác AOD với diện tích tam giác BOC?
Vì AB//CD
nên \(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
Ta có: \(\dfrac{S_{BOA}}{S_{BOC}}=\dfrac{OA}{OC}\)
\(\dfrac{S_{BOA}}{S_{AOD}}=\dfrac{OB}{OD}\)
mà \(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
nên \(S_{BOC}=S_{AOD}\)
Hình thang ABCD có tỉ số 2 đáy AB và CD là 2/3 . hai đường chéo cắt nhau ở điểm O .
A , So sánh diện tích tam giác AOD và diện tích tam giác BOC
B , Cho biết diện tích tam giác AOB là 4cm2. tính diện tích hình thang ABCD ?
\(ABssCD\Rightarrow\dfrac{AB}{CD}=\dfrac{OB}{OD}=\dfrac{OA}{OC}=\dfrac{2}{3}\)
a)\(S_{AOD}=\dfrac{1}{2}OA.OD.sinAOB\)
\(S_{BOC}=\dfrac{1}{2}OB.OC.sinBOC\)
\(\Rightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{OA.OD}{OB.OC}\) vì \(\widehat{AOD}=\widehat{BOC}\Rightarrow sinAOD=sinBOC\)
\(\Leftrightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{2}{3}.\dfrac{3}{2}=1\)
b) vì \(ABssCD\Rightarrow\dfrac{OH}{OK}=\dfrac{2}{3}\Rightarrow\dfrac{OH}{HK}=\dfrac{2}{5}\)
\(S_{AOB}=\dfrac{1}{2}.OH.AB\\ S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{1}{2}\left(AB+\dfrac{3}{2}AB\right).HK=\dfrac{1}{2}.\dfrac{5}{2}AB.HK\)
\(\Rightarrow\dfrac{S_{AOB}}{S_{ABCD}}=\dfrac{\dfrac{1}{2}OH.AB}{\dfrac{1}{2}HK.\dfrac{5}{2}AB}=\dfrac{2}{5}.\dfrac{1}{\dfrac{5}{2}}=\dfrac{4}{25}\)
\(\Rightarrow S_{ABCD}=\dfrac{4}{\dfrac{4}{25}}=25\)
Cho hình thang ABCD có hai đáy AB và CD( đáy lớn CD dài gấp 2 lần đáy nhỏ AB).Hai đường chéo AC và BD cắt nhau tại O.
a) Hãy so sánh diện tích của hai hình tam giác ABC và BCD ?
b) Hãy chứng tỏ diện tích của hình tam giác AOD bằng diện tích hình tam giác BOC ?
Kẻ \(AH\perp BC\)
Ta có :\(S_{ABC}=AH.BC\)
\(S_{BCD}=AH.BC\)
\(\Rightarrow S_{ABC}=S_{BCD}\)
b, Theo câu a ta có \(S_{ABC}=S_{BCD}\)
\(\Rightarrow S_{ABC}-S_{DOC}=S_{BCD}-S_{DOC}\)
\(\Rightarrow S_{AOD}=S_{BOC}\left(ĐPCM\right)\)
cho hình thang ABCD có đáy AB=1/2CD diện tích tam giác ABD là 25 cm2 . AC cắt BD tại O
a/ tính diện tích hình thang ABCD
b/ so sánh diện tích tam giác AOD và diện tích tam giác BOC
Cho 1 hình thang có 2 đáy CD bằng AB*2. Vẽ AC cách BD cách nhau tại O. Biết diện tích hình tam giác BOC là 12 cm vuông?
A. so sánh diện tích hình tam giác AOD và BOC .
B. Tính diện tích hình thang
Cho hình thang ABCD. Hai đường chéo AC và BD cắt nhau tại O. Hãy so sánh diện tích hình tam giác AOD và BOC.
Bài giải dài lắm xin lỗi bạn nha. Nếu được thì cho mình địa chỉ mail nhé. Mình gửi lời giải cho
cho hình thang ABCD có đáy AB bằng 1/3 CD. Các đoạn thẳng AC và BD cắt nhau tại điểm O. Biết diện tích hình tam giác BOC là 12cm2
a) so sánh diện tích hình tam giác BOC và tam giác ABC.
b) So sánh diện tích hình tam giác ABC với hình thang ABCD.
c) So sánh diện tích hình tam giác AD và diện tích hình tam giác BOC.
a: Xét ΔOBA và ΔODC có
góc OBA=góc ODC
góc BOA=góc DOC
=>ΔOBA đồng dạng với ΔODC
=>OB/OD=OA/OC=AB/CD=1/3
=>S ABO=1/3*S ABC
=>S BOC=2/3*S ABC
b: Kẻ CH vuông góc AB
=>S ABC=1/2*CH*AB
S ABCD=1/2*CH*(AB+CD)
=>S ABC/S ABCD=AB/(AB+CD)
cho hình thang ABCD có hai đáy là đáy bé AB=1/3 đáy lớn CD
a, so sánh diện tích tam giác ABC và ABD?
b, so sánh diện tích tam giác ACD và BCD?
c, so sánh diện tích tam giác ACD và ABC
vẽ hình cho mình nha
