Cho hàm số y=mx-2 (m≠0)
a, Xác định m để đồ thị hàm số đồng biến, nghịch biến
b, Chứng minh đồ thị hàm số luôn đi qua điểm cố định với ∀ m
Những câu hỏi liên quan
Cho hàm số y=(m-3x)
a) Với giá trị nào của m thì hàm số đồng biến ?Nghịch biến?
b) Xác định giá trị của m để đồ thị của hàm số đi qua điểm A(1:2)
c) Xác định giá trị của m để đồ thị của hàm số đi qua điểm B(1:-2)
: Cho hàm số : y = (m – 5)x
⦁ Với giá trị nào của m thì hàm số đồng biến ? Nghịch biến ?
⦁ Xác định giá trị của m để đồ thị hàm số đi qua điểm A(1 ; 2)
⦁ Vẽ đồ thị hàm số đã tìm được ở câu b)
Để hàm số y=(m-5)x là hàm số bậc nhất thì \(m-5\ne0\)
hay \(m\ne5\)
1) Để hàm số y=(m-5)x đồng biến trên R thì m-5>0
hay m>5
Để hàm số y=(m-5)x nghịch biến trên R thì m-5<0
hay m<5
2) Để đồ thị hàm số y=(m-5)x đi qua A(1;2) thì
Thay x=1 và y=2 vào hàm số y=(m-5)x, ta được:
m-5=2
hay m=7(nhận)
Vậy: Để đồ thị hàm số y=(m-5)x đi qua A(1;2) thì m=7
Đúng 2
Bình luận (1)
Cho hàm số y=(m-3)x
a)Với giá trị nào của m thì hàm số đồng biến ? Hàm số nghịch biến ?
b)Xác định giá trị của m để đồ thị hàm số đi qua A(1;2)
c)Xác định giá trị của m để đồ thị hàm số đi qua B(1;-2).giúp mình .
Cho hàm số bậc nhất : y=(m^2+1)x-1
a, Hàm số đã cho đồng biến hay nghịch biến ? Vì sao
b, Chứng tỏ rằng đồ thị hàm số đã cho luôn đi qua 1 điểm cố định ( x0;y0) với mọi m
Câu a :))
Hàm số đã cho đồng biến .
giải thích :
Do \(m^2\ge0\forall m\)
\(\Rightarrow m^2+1>0\)
Vậy hàm số trên đồng biến.
Đúng 0
Bình luận (0)
Giả sử đths đi qua điểm cố định ( x0;y0 )
Ta có y0 = ( m2 +1 )x0 - 1
<=> y0 = m2 x0 +x0 -1
<=> y0 -x0 +1 -m2x0 = 0
Để pt nghiệm đúng với mọi m \(\Leftrightarrow\hept{\begin{cases}y_0-x_0+1=0\\x_0=0\end{cases}\Leftrightarrow\hept{\begin{cases}y_0=-1\\x_0=0\end{cases}}}\)
Vậy đths luôn đi qua điểm cố định ( 0 ; -1 )
Đúng 0
Bình luận (0)
Cho hàm số y=(m-1)x-5
a) Xác định m để hàm số đồng biến nghịch biến
b) Xác định m để đô thị hàm số đi qua điểm A(1;-3)
c) Vẽ đồ thị hàm số ứng với m tìm được ở câu b
Cho hàm số : y=(m-1)x+2-m (1)
(Với m≠1) có đồ thị là d
a) tìm m để hàm số (1) đồng biến, nghịch biến
b) vẽ đồ thị hàm số khi M=0
c) tìm điểm cố định của (1) đi qua với mọi m
a: Để (1) đồng biến thì m-1>0
=>m>1
Để (1) nghịch biến thì m-1<0
=>m<1
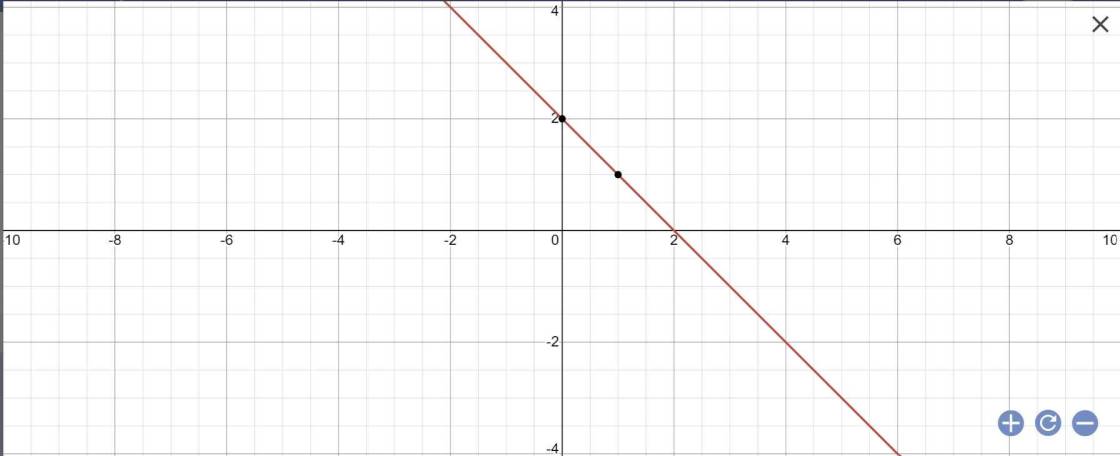
b: Khi m=0 thì (1) sẽ là y=-x+2
c: y=(m-1)x+2-m
=mx-x+2-m
=m(x-1)-x+2
Điểm mà (1) luôn đi qua là:
x-1=0 và y=-x+2
=>x=1 và y=-1+2=1
Đúng 1
Bình luận (0)
Cho hàm số y=2mx-2m-1 (m khác 0)
a) Xác định m để đò thị hàm số đi qua gốc tọa độ O
b) Gọi A, B lần lượt là giao điểm của đồ thị hàm số với các trục Ox, Oy. Xác định m để diện tích tam giác AOB bằng 4( đvdt )
c) Chứng minh rằng đồ thị hàm số luôn đi qua 1 điểm cố định
sr nha em ko làm dc
Mọi người giúp em với ạ,em cảm ơn !Bài 1: Cho đường thẳng d, y(m-1)x+ma)Tìm m để hàm số nghịch biến trên Rb) tìm m để đồ thị hàm số đi qua gốc tọa độc) Với m2,vẽ đồ thị hàm sốd) Chứng tỏ rằng đường thẳng d luôn luôn đi qua 1 điểm cố định với mọi m,Tìm điểm đóBài 2: Cho 3 điểm A(2;4),B(-3;-1),C(2;1).Hãy chứng minh 3 điểm thẳng hàngBài 3: Cho hàm số yax-4a) Tìm a biết đồ thị hàm số đi qua điểm M(2;5)b)Vẽ đồ thị hàm số vừa tìm đượcBài 4 : Tìm hàm số yax+b,biết đồ thị hàm số của nó đi qua 2 điểm A(2...
Đọc tiếp
Mọi người giúp em với ạ,em cảm ơn !
Bài 1: Cho đường thẳng d, y=(m-1)x+m
a)Tìm m để hàm số nghịch biến trên R
b) tìm m để đồ thị hàm số đi qua gốc tọa độ
c) Với m=2,vẽ đồ thị hàm số
d) Chứng tỏ rằng đường thẳng d luôn luôn đi qua 1 điểm cố định với mọi m,Tìm điểm đó
Bài 2: Cho 3 điểm A(2;4),B(-3;-1),C(2;1).Hãy chứng minh 3 điểm thẳng hàng
Bài 3: Cho hàm số y=ax-4
a) Tìm a biết đồ thị hàm số đi qua điểm M(2;5)
b)Vẽ đồ thị hàm số vừa tìm được
Bài 4 : Tìm hàm số y=ax+b,biết đồ thị hàm số của nó đi qua 2 điểm A(2;5) và B(-2;-3)
Cho hàm số y = -6x+m-1 (1) và y = (m-1)x+(3m-11) (2)
a, Hàm số (1) là hàm số đồng biến hay nghịch biến trên R ?
Xác định hàm số (1) biết rằng đồ thị hàm số (1) đi qua điểm A(-1;6)
b, Tìm m để đồ thị hàm số (1) cắt đồ thị hàm số (2) tại một điểm nằm tên trục tung , tìm tọa độ giao điểm đó .
a, Vì \(-6< 0\)nên hàm số (1) là hàm nghịch biến
Vì \(A\left(-1;6\right)\in\left(1\right)\)
\(\Rightarrow6=\left(-6\right).\left(-1\right)+m-1\)
\(\Leftrightarrow6=6+m-1\)
\(\Leftrightarrow m=1\)
b, Đths (1) cắt đths 2 tại 1 điểm trên trục tung nên
\(\hept{\begin{cases}m-1\ne3m-11\\x=0\\-6x+m-1=\left(m-1\right)x+3m-11\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m-1\ne3m-11\\m-1=3m-11\end{cases}}\)ko tìm đc m
Đúng 0
Bình luận (0)