Đường tròn (C): x 2 + y 2 + 4 x − 2 y − 4 = 0  có tâm I(-2; 1) và bán kính R = 3.

Ta có : I M = 1 + 2 2 + 2 − 1 2 = 10 > 3  nên M nằm ngoài đường tròn.

Qua M kẻ được hai tiếp tuyến đến đường tròn.

ĐÁP ÁN C

Đường tròn đã cho có tâm  I    − 3 2   ;     5 2

Bán kính đường tròn  là:   R ​ =    − 3 2 2 + ​   5 2 2 + ​ 2 = 21 2

Độ dài  I M ​ =     − 2 + ​ 3 2 2 + ​   1 − 5 2 2 =    5 2    < ​​ R

Do đó, điểm  M nằm trong đường tròn. 

Qua M không kẻ được tiếp tuyến nào đến đường tròn.

ĐÁP ÁN A

a) x2 + y2 – 4x + 8y – 5 = 0

⇔ (x2 – 4x + 4) + (y2 + 8y + 16) = 25

⇔ (x – 2)2 + (y + 4)2 = 25.

Vậy (C) có tâm I(2 ; –4), bán kính R = 5.

b) Thay tọa độ điểm A vào phương trình đường tròn ta thấy:

(–1 – 2)2 + (0 + 4)2 = 32 + 42 = 52= R2

⇒ A thuộc đường tròn (C)

⇒ tiếp tuyến (d’) cần tìm tiếp xúc với (C) tại A

⇒ (d’) là đường thẳng đi qua A và vuông góc với IA

⇒ (d’) nhận 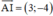 là một vtpt và đi qua A(–1; 0)

⇒ phương trình (d’): 3(x + 1) – 4(y - 0)= 0 hay 3x – 4y + 3 = 0.

c) Gọi tiếp tuyến vuông góc với (d) : 3x – 4y + 5 = 0 cần tìm là (Δ).

(d) có 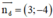 là một vtpt; 1 VTCP là ud→(4; 3)

(Δ) ⊥ (d) ⇒ (Δ) nhận 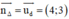 là một vtpt

⇒ (Δ): 4x + 3y + c = 0.

(C) tiếp xúc với (Δ) ⇒ d(I; Δ) = R

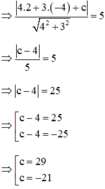
Vậy (Δ) : 4x + 3y + 29 = 0 hoặc 4x + 3y – 21 = 0.

Đáp án: D

Phương trình đường thẳng d đi qua điểm (1;2) có dạng: a(x - 1) + b(y - 2) = 0

Ta có:

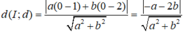
Vì d tiếp xúc với (C) nên: d(I;d) = R

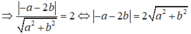
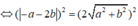
⇔  a 2  + 4ab + 4 b 2  = 4 a 2  + 4 b 2  ⇔ 3 a 2  - 4ab = 0

⇔ a(3a - 4b) = 0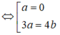 

Với a = 0 chọn b = 1 ⇒ d: y - 2 = 0

Với 3a = 4b chọn a = 4, b = 3 ⇒ d: 4(x - 1) + 3(y - 2) = 0 ⇔ 4x + 3y - 10 = 0

x 2 + y 2 + 4 x − 2 y − 4 = 0  và điểm M(-2; 4)

Đường tròn (C): x 2 + y 2 + 4 x - 2 y - 4 = 0  có tâm I(-2;1) và bán kính  R =    ( − 2 ) 2 + ​ 1 2 + ​ 4 = 3

 Phương trình tiếp tuyến tại M(- 2; 4) và nhận    I M →    ( 0 ;     3 ) ​ làm VTPT là: 

0( x +2) + 3 (y – 4) = 0 hay y = 4

ĐÁP ÁN D

ĐÁP ÁN B

Đường tròn (C): x 2   +   y 2   -     4 x   +   2 y   –   4 =   0  có tâm I(2; -1) và  bán kính  R ​ =    2 2 + ​ ( − 1 ) 2 + ​ 4 = 3

 Tiếp  tuyến qua M( -4; 2)  và nhận n →    ( a ;    b )  làm VTPT có phương trình :

a( x+ 4) + b (y – 2)= 0  hay ax + by + 4a – 2b = 0    (*)

Khoảng cách từ tâm I đến  tiếp tuyến bằng bán kính nên ta có:

d ( I ;    d ) ​ =     R ⇔ 2 a − b + ​ 4 a − ​​ 2 b a 2 + ​ b 2 = 3 ⇔ 6 a − 3 b a 2 + ​ b 2 = 3 ⇔ 2 a − b a 2 + ​ b 2 = 1 ⇔ 2 a − b = a 2 + ​ b 2 ⇔ 4 a 2 − 4 a b + ​ b 2 = a 2 + ​ b 2 ⇔ 3 a 2 − 4 a b = 0 ⇔ a ( ​ 3 a − 4 b ) = 0 ⇔ a = 0 3 a = 4 b

* Nếu a= 0 , chọn  b= 1 thay  vào (*) ta có phương trình tiếp tuyến là:  y – 2= 0

* Nếu 3a =  4b, chọn a = 4 thì b = 3 thay vào (*) ta có phương trình tiếp tuyến là: 

4x + 3y + 10 = 0

Vậy có 2 tiếp tuyến qua M là:  y – 2= 0 và 4x +3y + 10= 0

Đáp án: B

(C): x 2  + y 2  - 2x - 4y - 4 = 0 ⇔ (x - 1 ) 2  + (y - 2 ) 2  = 9

Đường tròn (C) có tâm I(1;2)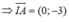 

Tiếp tuyến của đường tròn tại A là đường thẳng đi qua A và nhận IA làm vecto pháp tuyến: -3(y + 1) = 0 ⇔ y + 1 = 0

Đáp án A

a) Để tìm phương trình đường tròn © có tâm I(2,3) đi qua điểm A(5,7), ta sử dụng công thức khoảng cách từ điểm đến tâm đường tròn:

$I\hat{A} = \sqrt{(x_A - x_I)^2 + (y_A - y_I)^2}$

Với I là tâm đường tròn, A là điểm trên đường tròn.

Ta có: $x_I = 2$, $y_I = 3$, $x_A = 5$, $y_A = 7$

Thay vào công thức ta được:

$\sqrt{(5-2)^2 + (7-3)^2} = \sqrt{34}$

Vậy bán kính của đường tròn là $\sqrt{34}$.

Phương trình đường tròn © có tâm I(2,3) và bán kính $\sqrt{34}$ là:

$(x-2)^2 + (y-3)^2 = 34$

b) Để tìm phương trình tiếp tuyến của đường tròn © : $(x-1)^2 + ( y+5)^2 =4$, ta cần tìm đạo hàm của phương trình đường tròn tại điểm cần tìm tiếp tuyến.

Ta có phương trình đường tròn chính giữa:

$(x-1)^2 + (y+5)^2 = 2^2$

Đạo hàm hai vế theo x:

$2(x-1) + 2(y+5)y' = 0$

Suy ra:

$y' = -\frac{x-1}{y+5}$

Tại điểm M(x,y) trên đường tròn, ta có:

$(x-1)^2 + (y+5)^2 = 2^2$

Đạo hàm hai vế theo x:

$2(x-1) + 2(y+5)y' = 0$

Suy ra:

$y' = -\frac{x-1}{y+5}$

Vậy tại điểm M(x,y), phương trình tiếp tuyến của đường tròn là:

$y - y_M = y'(x-x_M)$

Thay $y'$ bằng $\frac{-(x-1)}{y+5}$ và $x_M$, $y_M$ bằng 1, -5 ta được:

$y + 5 = \frac{-(x-1)}{y+5}(x-1)$

Simplifying:

$x(y+5) + y(x-1) = 6$

Đường thẳng (d) có phương trình là $3x + 4y - 1 = 0$. Vì tiếp tuyến song song với đường thẳng (d) nên hệ số góc của tiếp tuyến