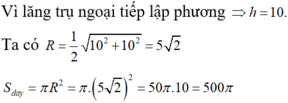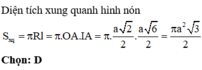một hình vuông có diện tích 50cm2.Tính thể tích hình cầu khi quay nửa đường tròn ngoại tiếp hình vuông đó

Những câu hỏi liên quan
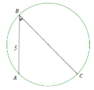
Cho tam giác ABC vuông cân tại A có cạnh góc vuông bằng a. Tính diện tích mặt cầu được tạo thành khi quay nửa đường tròn ngoại tiếp tam giác ABC một vòng quanh cạnh BC
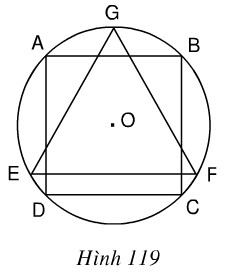
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.Hình 119
Đọc tiếp
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
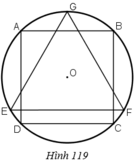
Hình 119
Cho hình vuông ABCD nội tiếp đưòng tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đuờng tròn đó, EF là dây song song với AB. Cho hình đó quay xung quanh trục GO. Chứng minh:a, Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh rab, Bình phương diện tích toàn phần của hình trụ bằng tích diện tích hình cầu và diện tích toàn phần của hình nón
Đọc tiếp
Cho hình vuông ABCD nội tiếp đưòng tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đuờng tròn đó, EF là dây song song với AB. Cho hình đó quay xung quanh trục GO. Chứng minh:
a, Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra
b, Bình phương diện tích toàn phần của hình trụ bằng tích diện tích hình cầu và diện tích toàn phần của hình nón
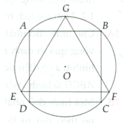
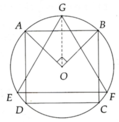
a, V h t A B C D = π AB 2 2 . BC = π AB 3 4 = π 2 2 . R 3 (1)
V h c = 4 3 πR 3 (2)
V h n = 1 3 π EF 2 2 . GH = 1 8 3 π . EF 3 . Tính được GO = 3 R
=> V h n = 1 8 3 π 3 3 R 3 = 3 8 πR 3 (3)
Từ (1), (2) và (3) => ĐPCM
b, S t p h t = 3 πR 2 (4); S h c = 4 πR 2 (5)
S t p h n = 3 4 πEF 2 = 3 4 π . 3 R 2 = 9 4 πR 2 (6)
Từ (4); (5) và (6) => ĐPCM
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB5,
A
B
C
^
30
°
. Hình cầu tạo bởi đường tròn ngoại tiếp tam giác ABC quay quanh BC có diện tích là.
Đọc tiếp
Cho tam giác ABC vuông tại A có AB=5,
A B C ^ = 30 ° . Hình cầu tạo bởi đường tròn ngoại
tiếp tam giác ABC quay quanh BC có diện tích là.
![]()
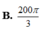
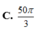
![]()
Cho tam giác ABC vuông tại A có
A
B
5
,
A
B
C
30
o
. Hình cầu tạo bởi đường tròn ngoại tiếp tam giác ABC quay quanh BC có diện tích là A.
100
π
3...
Đọc tiếp
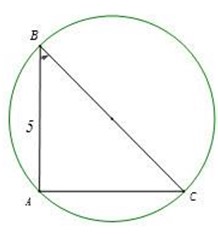
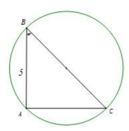
Cho tam giác ABC vuông tại A có A B = 5 , A B C = 30 o . Hình cầu tạo bởi đường tròn ngoại tiếp tam giác ABC quay quanh BC có diện tích là
A. 100 π 3
B. 200 π 3
C. 50 π 3
D. Kết quả khác
Đáp án A
Ta có đường tròn ngoại tiếp tam giác ABC có tâm là trung điểm BC
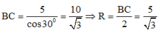

Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB5,
A
B
C
30
°
. Hình cầu tạo bởi đường tròn ngoại tiếp tam giác ABC quay quanh BC có diện tích là A.
100
π
3
B.
200
π
3
C.
50
π
3
D. Kết quả khác
Đọc tiếp
Cho tam giác ABC vuông tại A có AB=5, A B C = 30 ° . Hình cầu tạo bởi đường tròn ngoại tiếp tam giác ABC quay quanh BC có diện tích là
A. 100 π 3
B. 200 π 3
C. 50 π 3
D. Kết quả khác
Cho hình trụ có hai đường tròn đáy lần lượt ngoại tiếp hai hình vuông đối diện của một hình lập phương có cạnh 10cm. Tính thể tích khối trụ.
A
.
250
πcm
3
B
.
300
πcm
3
C
.
1000
πcm
3
D
.
500
πcm...
Đọc tiếp
Cho hình trụ có hai đường tròn đáy lần lượt ngoại tiếp hai hình vuông đối diện của một hình lập phương có cạnh 10cm. Tính thể tích khối trụ.
A . 250 πcm 3
B . 300 πcm 3
C . 1000 πcm 3
D . 500 πcm 3
Tam giác vuông cân ABC ngoại tiếp đường tròn tâm I (như hình vẽ). Cho nửa đường tròn (phần gạch sọc) và tam giác AHC quay quanh AH tạo thành các khối tròn xoay quanh có thể tích là
V
1
,
V
2
. Tính
k
V
1
V
2
.
Đọc tiếp
Tam giác vuông cân ABC ngoại tiếp đường tròn tâm I (như hình vẽ). Cho nửa đường tròn (phần gạch sọc) và tam giác AHC quay quanh AH tạo thành các khối tròn xoay quanh có thể tích là V 1 , V 2 . Tính k = V 1 V 2 .

![]()
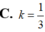
![]()
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a. Một hình nón có đỉnh là tâm của hình vuông
A
B
C
D
và có đường tròn đáy ngoại tiếp hình vuông ABCD. Tính diện tích xung quanh của hình nón đó. A.
π
a
2...
Đọc tiếp
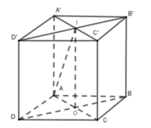
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Một hình nón có đỉnh là tâm của hình vuông A ' B ' C ' D ' và có đường tròn đáy ngoại tiếp hình vuông ABCD. Tính diện tích xung quanh của hình nón đó.
A. π a 2 2 2
B. π a 2 3
C. π a 2 2 4
D. π a 2 3 2
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h. 119). Cho hình đó quay xung quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
Đọc tiếp
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h. 119). Cho hình đó quay xung quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
-0132.jpg)
Hướng dẫn trả lời:
Hình a.
V=π(12,62)2.8,4+12.43π(12,62)3=13π(6,9)2.(8,4+12,63)=500,094π(cm3)V=π(12,62)2.8,4+12.43π(12,62)3=13π(6,9)2.(8,4+12,63)=500,094π(cm3)
Vậy Vhình a = 500,094π cm3
Hình b.
V=13π(6,9)2.20+12.43π.(6,9)3=13π(6,9)2(20+13,8)=536,406π(cm3)V=13π(6,9)2.20+12.43π.(6,9)3=13π(6,9)2(20+13,8)=536,406π(cm3)
Vậy Vhình b = 536, 406π cm3
Hình c.
V=13π.22.4+π.22.4+12.43π.23=4.22.π(13+1+13)=80π3(cm3)V=13π.22.4+π.22.4+12.43π.23=4.22.π(13+1+13)=80π3(cm3)
Vậy Vhình c =
Đúng 0
Bình luận (0)
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
Hướng dẫn trả lời:
a) Thể tích hình trụ được tạo bởi hình vuông ABCD là:
V=π(AB2)2.BCV=π(AB2)2.BC với AB là đường chéo của hình vuông có cạnh là R và AB = R√2 (=BC)
V=π(R√22)2.R√2=π.2R24.R√2=πR3√22⇒V2=(πR3√222)=2π2R62(1)V=π(R22)2.R2=π.2R24.R2=πR322⇒V2=(πR3222)=2π2R62(1)
Thể tích hình cầu có bán kính R là: V1=43πR3V1=43πR3
Thể tích hình nón có bán kính đường tròn đáy bằng EF2EF2 là:
V2=13π(EF2)2.GHV2=13π(EF2)2.GH
Với EF = R√3 (cạnh tam giác đều nội tiếp trong đường tròn (O;R))
và GH=EF√32=R√3.√32=3R2GH=EF32=R3.32=3R2
Thay vào V2, ta có: V2=13π(R√32)2.3R2=38πR3V2=13π(R32)2.3R2=38πR3
Ta có: V1V2=43πR3.38πR3=π2R62(2)V1V2=43πR3.38πR3=π2R62(2)
So sánh (1) và (2) ta được : V2 = V1. V2
b) Diện tích toàn phần của hình trụ có bán kính AB2AB2 là:
S=2π(AB2).BC+2π(AB2)2S=2π.R√22R√2+2π(R√22)2S=2πR2+πR2=3πR2⇒S2=(3πR2)2=9π2.R4(1)S=2π(AB2).BC+2π(AB2)2S=2π.R22R2+2π(R22)2S=2πR2+πR2=3πR2⇒S2=(3πR2)2=9π2.R4(1)
Diện tích mặt cầu có bán kính R là: S1 = 4πR2 (2)
Diện tích toàn phần của hình nón là:
S2=πEF2.FG+π(EF2)2=πR√32.R√3+π(R√32)2=9πR24S2=πEF2.FG+π(EF2)2=πR32.R3+π(R32)2=9πR24
Ta có: S1S2=4πR2.9πR24=9π2R4(2)S1S2=4πR2.9πR24=9π2R4(2)
So sánh (1) và (2) ta có: S2 = S1. S2
Đúng 0
Bình luận (0)