cho tam giác ABC có 3 góc A,B,C thỏa \(sinA+sinB=cosA+cosB\)
tính giá trị góc C
Những câu hỏi liên quan
cho tam giác abc có 3 góc nhọn. Vẽ đường cáo AD, BE, CF cắt nhau tại H. Chứng minh:
a) \(0< cos^2A+cos^2B+cos^2C< 1\)
b)\(2< sin^2A+sin^2B+sin^2C< 3\)
c)sinA + sinB + sinC < 2( cosA + cosB + cosC)
d)sinB . cosC + sinC . cosB = sinA
e)tanA + tanB + tanC = tanA . tanB . tanC
Tìm tính chất của tam giác ABC thỏa:
sinA+sinB+sinC=1-cosA+cosB+cosC
TL:
sinA+sinB+sinC=1-cosA+cosB+cosC => Tam giác ABC Vuông tại A
Vế trái = sinA + sinB + sinC
= 2sin(A + B)/2.cos(A - B)/2 + 2sinC/2.cosC/2
= 2cosC/2.cos(A - B)/2 + 2sinC/2.cosC/2
= 2cosC/2[cos(A - B)/2 + sinC/2]
=2.cosC/2.[cos(A - B)/2 + cos(A + B)/2]
= 4.cosC/2.cosB/2.cosA/2
Vế phải = 1 - cosA + cosB + cosC
= 2sin²A/2 + 2cos(B + C)/2.cos(B - C)/2
= 2.sinA/2[sinA/2 + cos(B - C)/2] (vì cos(B + C)/2 = sinA/2)
= 2.sinA/2[cos(B + C)/2 + cos(B - C)/2
= 4.sinA/2.cosB/2.cosC/2
Vậy sinA + sinB + sinC = 1 - cosA + cosB + cosC
<=> cosA/2.cosB/2.cosC/2 = sinA/2.cosB/2.cosC/2
<=> cosB/2.cosC/2(sinA/2 - cosA/2) = 0
mà cosB/2 ≠ 0 và cosC/2 ≠ 0
=> sinA/2 = cosA/2
<=> A/2 = 45o
<=> A = 90o
tam giác ABC vuông tại A
SinA+SinB+SinC > 2.Với A,B,C là ba góc nhọn trong tam giác.
CosA+CosB+CosC <= 2/3.Với A,B,C là ba góc nhọn trong tam giác.
CotA+CotB+CotC <= căn bậc hai của 3.Với A,B,C là ba góc nhọn trong tam giác.
Cho tam giác ABC có sinA+sinB= cosA+cosB. Chứng minh rằng tam giác ABC vuông.
1) ta co ket qua nhu sau:
sinAcosA+cosAcosB = sinAsinB+sinAcosA
<=> cosAcosB-sinAsinB=0
<=>cos(A+B)=0
<=> -cosC=0 (vi A+B+C=180)
hay cosC=0 => C=90
Đúng 0
Bình luận (0)
Cho A, B, C là 3 góc trong tam giác. Chứng minh rằng:1, sin A + sin B - sin C 4sindfrac{A}{2} sin dfrac{B}{2}sin dfrac{C}{2}2, dfrac{sinA+sinB-sinC}{cosA+cosB-cosC+1}tandfrac{A}{2}tandfrac{B}{2}tandfrac{C}{2} (ΔABC nhọn)3, dfrac{cosA+cosB+cosC+3}{sinA+sinB+sinC}tandfrac{A}{2}+tandfrac{B}{2}+tandfrac{C}{2}GIÚP MÌNH VỚI!!!
Đọc tiếp
Cho A, B, C là 3 góc trong tam giác. Chứng minh rằng:
1, sin A + sin B - sin C = 4sin\(\dfrac{A}{2}\) sin \(\dfrac{B}{2}\)sin \(\dfrac{C}{2}\)
2, \(\dfrac{sinA+sinB-sinC}{cosA+cosB-cosC+1}=tan\dfrac{A}{2}tan\dfrac{B}{2}tan\dfrac{C}{2}\) (ΔABC nhọn)
3, \(\dfrac{cosA+cosB+cosC+3}{sinA+sinB+sinC}=tan\dfrac{A}{2}+tan\dfrac{B}{2}+tan\dfrac{C}{2}\)
GIÚP MÌNH VỚI!!!
1.
\(sinA+sinB-sinC=2sin\dfrac{A+B}{2}.cos\dfrac{A-B}{2}-sin\left(A+B\right)\)
\(=2sin\dfrac{A+B}{2}.cos\dfrac{A-B}{2}-2sin\dfrac{A+B}{2}.cos\dfrac{A+B}{2}\)
\(=2sin\dfrac{A+B}{2}.\left(cos\dfrac{A-B}{2}-cos\dfrac{A+B}{2}\right)\)
\(=2sin\dfrac{A+B}{2}.2sin\dfrac{A}{2}.sin\dfrac{B}{2}\)
\(=4sin\dfrac{A}{2}.sin\dfrac{B}{2}.cos\dfrac{C}{2}\)
Sao t lại đc như này v, ai check hộ phát
Đúng 0
Bình luận (0)
Tính giá trị biểu thức P ( sina + sinb) 2+ ( cosa + cosb) 2 biết a - b
π
4
Đọc tiếp
Tính giá trị biểu thức P = ( sina + sinb) 2+ ( cosa + cosb) 2 biết a - b = π 4
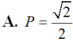
Chọn C.
Theo giả thiết ta có:
P = ( sina + sinb) 2 + ( cosa + cosb) 2
= sin2a + 2.sina.sinb + sin2b + cos2a + 2cosa. cosb + cos2b
= 2 + 2( sina.sinb + cos a. cosb)
= 2 + 2.cos( a - b) ( sử dụng công thức cộng)
Đúng 0
Bình luận (0)
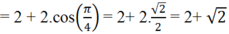
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).
a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại C . Hãy tinhs sinA,cosA,tgA,sinB,cosB,tgB,cotgB biết cotgA=1
a,cho sina+sinb=√2/2
cosa+cosb=√6/2
tinh sin(a-b)
b, cho sina+cosb=3/2
sinb+cosa=-1/3
tinh sin(a+b)