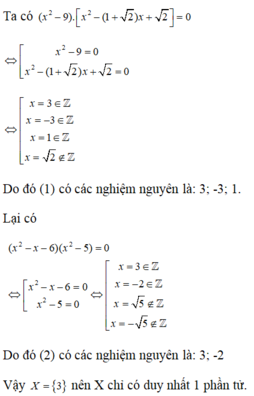X64=x63+x62+x^61+......+x2+x+2=0 Giải phương nghiệm nguyên

Những câu hỏi liên quan
Số nào trong ba số -1; 2 và -3 nghiệm đúng mỗi phương trình sau:
|x| = x (1), x2+5x+6=0(2)x2+5x+6=0(2) , 61−x=x+4(3)
Bài làm: (sai đâu chỉ giúp nha)
Trong ba số -1, 2 và -3 thì
+) x = 2 nghiệm đúng phương trình |x| = x vì |2| = 2 (đúng).
+) x = -3 nghiệm đúng phương trình 61−x=x+4(3)61−x=x+4(3)
Vì (−3)2+5.(−3)+6=0(−3)2+5.(−3)+6=0
9−15+6=09−15+6=0
0 = 0
+) x=−1x=−1 nghiệm đúng phương trình 61−x=x+461−x=x+4 vì:
61−(−1)=−1+4⇔62=3⇔3=3
Đúng 0
Bình luận (0)
1) Giải phương trình: x(x-3)-(x+2)(x-1)=3 ta được nghiệm
2) Phương trình nào sau đây có 1 nghiệm
a) x(x-1)=0 b) (x+2)(x2+1)=0
c) x2-3x=0 d) x2-2x+3=0
1. x(x-3)-(x+2)(x-1)=3 <=> x2 - 3x - x2 - x + 2 = 3 => 4x = -1 => x = 1/4
2.
a) x = 0, x=1 (2 nghiệm, loại)
b) x2 + 1 > 0 => x = - 2 (1 nghiệm, chọn b)
c) <=> x(x-3) = 0 => x = 0, x=3 (2 nghiệm, loại)
d) (x-1)2 + 2 > 0 => Vô nghiệm (loại)
Đúng 0
Bình luận (0)
Gọi X là tập hợp các nghiệm nguyên chung của hai phương trình:
(
x
2
−
9
)
.
x
2
−
(
1
+
2
)
x
+
2
0
(1) và
(
x...
Đọc tiếp
Gọi X là tập hợp các nghiệm nguyên chung của hai phương trình: ( x 2 − 9 ) . x 2 − ( 1 + 2 ) x + 2 = 0 (1) và ( x 2 − x − 6 ) ( x 2 − 5 ) = 0 (2). Số phẩn tử của X là:
A. 0
B. 3
C. 2
D. 1
Giải phương trình nghiệm nguyên : x2 + 2y2 + 3xy - x = 2
Lời giải:
PT $\Leftrightarrow x^2+x(3y-1)+(2y^2-2)=0$
Coi đây là pt bậc 2 ẩn $x$ thì:
$\Delta=(3y-1)^2-4(2y^2-2)=y^2-6y+9=(y-3)^2$. Do đó pt có 2 nghiệm:
$x_1=\frac{1-3y+y-3}{2}=-y-1$
$x_2=\frac{1-3y+3-y}{2}=2-2y$
Đến đây bạn thay vô pt ban đầu để giải pt bậc 2 một ẩn thui.
Đúng 2
Bình luận (0)
Giải phương trình nghiệm nguyên 2x+5y+1)(2|x|+y+x+x2)=105
Cho phương trình 2 x 2 - x - 7 = 0, không giải phương trình
a) Chứng tỏ rằng phương trình có 2 nghiệm phân biệt x 1 , x 2
a) Ta có: a = 2; b = -1; c = -7
Δ = b 2 - 4ac = - 1 2 - 4.2.(-7) = 57 > 0
⇒ Phương trình có 2 nghiệm phân biệt x 1 , x 2
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị m nguyên để phương trình
x
+
2
+
2
−
x
+
2
−
x
2
+
4
−
2
m
+
3
0
có nghiệm A. 1 B. 3 C. 0 D. 2
Đọc tiếp
Có bao nhiêu giá trị m nguyên để phương trình x + 2 + 2 − x + 2 − x 2 + 4 − 2 m + 3 = 0 có nghiệm
A. 1
B. 3
C. 0
D. 2
Đặt t = x + 2 + 2 − x
Điều kiện t = x + 2 + 2 − x ≥ x + 2 + 2 − x = 2 ⇒ t ≥ 2
Lại có x + 2 + 2 − x ≤ 1 2 + 1 2 . x + 2 + 2 − x = 2 2 ⇒ t ≤ 2 2
Suy ra 2 ≤ t ≤ 2 2
Ta có: t 2 = 4 + 2 4 − x 2 ⇒ 2 4 − x 2 = t 2 − 4
Phương trình trở thành: t + t 2 − 4 − 2 m + 3 = 0 ⇔ t 2 + t − 2 m − 1 = 0
⇔ t 2 + t − 1 = 2 m *
Xét hàm số f ( x ) = t 2 + t − 1 (parabol có hoành độ đỉnh x = − 1 2 ∉ 2 ; 2 2 ) trên 2 ; 2 2 , có bảng biến thiên
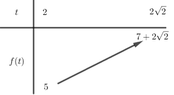
Phương trình (∗) có nghiệm thỏa 2 ≤ t ≤ 2 2 khi 5 ≤ 2 m ≤ 7 + 2 2
⇒ 5 2 ≤ m ≤ 7 + 2 2 2
5 2 ≤ m ≤ 7 + 2 2 2 → 2 , 5 ≤ m ≤ 4 , 91
Vậy có 2 giá trị m nguyên dương là m = 3 , m = 4
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
giải phương trình nghiệm nguyên : x2-x=y2-1
Giải phương trình:
20
(
x
-
2
x
+
1
)
2
-
5
(
x
+
2
x
-
1...
Đọc tiếp
Giải phương trình: 20 ( x - 2 x + 1 ) 2 - 5 ( x + 2 x - 1 ) 2 + 48 x 2 - 4 x 2 - 1 = 0 ta được các nghiệm x 1 , x 2 với x 1 < x 2 . Tính 3 x 1 - x 2
A. 25 3
B. -1
C. - 7 3
D. 1