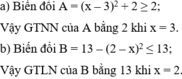Ta có: A = 4x - x2 = -(x2 - 4x) = -[(x2 - 4x + 4) - 4]

= -[(x - 2)2 - 4] = -(x - 2)2 + 4 ≤ 4

Vậy giá trị lớn nhất của A bằng 4 khi x - 2 = 0 hay x = 2.

\(x^2-4x+25\)

\(=\left(x^2-4x+4\right)+21\)

\(=\left(x-2\right)^2+21\)

\(\ge21\)

Bé hơn hoặc bằng 21 nha

Xin k

\(x^2-4x+25\)

\(=\left(x^2-4x+4\right)+21\)

\(=\left(x-2\right)^2+21\ge21\)

vậy giá trị nhỏ nhất của đa thức =21 khi x=2

Đàm Thu Thủy

x² - 4x + 25

= (x² + 4x + 4) + 21

= (x - 2)² + 21 \(\ge\) 21

Vậy giá trị nhỏ nhất của đa thức sẽ bằng 21 khi x = 2

x²-4x+25=(x²-4x+4)+21

             =(x-2)²+21

vì (x-2)²>=0 với mọi x

=>(x-2)²+21>=21 với mọi x

=>x²-4x+25>=21 với mọi x

dấu bằng xảy ra <=>(x-2)²=0

                         <=>x-2=0

                         <=>x=2

Đặt \(A=x^2-4x+25=x^2-4x+4+21=\left(x-2\right)^2+21\)

Ta co : \(\left(x-2\right)^2\ge0\forall x;\left(x-2\right)^2+21\ge21\forall x\)

Vậy GTNN A = 21 <=> x = 2 

Bài 2 : 

a, \(x^2-4x+4+1=\left(x-2\right)^2+1\ge1\)

Dấu ''='' xảy ra khi x = 2 

b, Ta có \(\left(x+1\right)^2+10\ge10\Rightarrow\dfrac{-100}{\left(x+1\right)^2+10}\ge-\dfrac{100}{10}=-10\)

Dấu ''='' xảy ra khi x = -1 

 Bài 1 : 

a, Ta có \(A\left(x\right)=x^2-4x+4=0\Leftrightarrow\left(x-2\right)^2=0\Leftrightarrow x=2\)

b, \(B\left(x\right)=x^2\left(2x+1\right)+\left(2x+1\right)=\left(x^2+1>0\right)\left(2x+1\right)=0\Leftrightarrow x=-\dfrac{1}{2}\)

c, \(C\left(x\right)=\left|2x-3\right|=\dfrac{1}{3}\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{1}{3}+3=\dfrac{10}{3}\\2x=-\dfrac{1}{3}+3=\dfrac{8}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\)

Ta có: A = 4x –  x 2  + 3

              = 7 –  x 2  + 4x – 4

              = 7 – ( x 2 – 4x + 4)

      = 7 – x - 2 2

Vì  x - 2 2  ≥ 0 với mọi x nên A = 7 –  x - 2 2  ≤ 7

Vậy giá trị của A lớn nhất là 7 khi x – 2 = 0 hay x = 2

`A=x^2-4x+1`
`=x^2-4x+4-3`
`=(x-2)^2-3>=-3`
Dấu "=" xảy ra khi x=2
`B=4x^2+4x+11`
`=4x^2+4x+1+10`
`=(2x+1)^2+10>=10`
Dấu "=" xảy ra khi `x=-1/2`
`C=(x-1)(x+3)(x+2)(x+6)`
`=[(x-1)(x+6)][(x+3)(x+2)]`
`=(x^2+5x-6)(x^2+5x+6)`
`=(x^2+5x)^2-36>=-36`
Dấu "=" xảy ra khi `x=0\or\x=-5`
`D=5-8x-x^2`
`=21-16-8x-x^2`
`=21-(x^2+8x+16)`
`=21-(x+4)^2<=21`
Dấu "=" xảy ra khi `x=-4`
`E=4x-x^2+1`
`=5-4+4-x^2`
`=5-(x^2-4x+4)`
`=5-(x-2)^2<=5`
Dấu "=" xảy ra khi `x=5`

A= x² - 4x +1

   = x² - 4x + 4 - 3

   = (x-2)² -3

Ta có (x-2)² ≥ 0 ∀ x

    ⇒ (x-2)² -3 ≥ -3 ∀ x

Vậy A_Min= -3 tại x=2

B= 4x²+4x+11

  = 4x²+4x+1+10

  = (2x+1)²+10

Ta có (2x+1)² ≥ 0 ∀ x

     ⇒ (2x+1)²+10 ≥ 10 ∀ x

Vậy B_Min=10 tại x= \(\dfrac{-1}{2}\)

C=(x-1)(x+3)(x+2)(x+6)

  = (x-1)(x+6)(x+3)(x+2)

  = (x²+5x-6) (x²+5x+6)

  = (x²+5x)² -36

Ta có (x²+5x)² ≥ 0 ∀ x
  ⇒ (x²+5x)² -36 ≥ -36 ∀ x

Vậy C_Min=-36 tại x=0 hoặc x= -5

Tính giá trị nhỏ nhất:

\(A=x^2-4x+1=(x^2-4x+4)-3=(x-2)^2-3\)

Vì $(x-2)^2\geq 0, \forall x\in\mathbb{R}$ nên $A=(x-2)^2-3\geq 0-3=-3$

Vậy $A_{\min}=-3$

Giá trị này đạt tại $(x-2)^2=0\Leftrightarrow x=2$

$B=4x^2+4x+11=(4x^2+4x+1)+10=(2x+1)^2+10\geq 0+10=10$
Vậy $B_{\min}=10$ 

Giá trị này đạt tại $(2x+1)^2=0\Leftrightarrow x=-\frac{1}{2}$
$C=(x-1)(x+3)(x+2)(x+6)$

$=(x-1)(x+6)(x+3)(x+2)$
$=(x^2+5x-6)(x^2+5x+6)$

$=(x^2+5x)^2-36\geq 0-36=-36$

Vậy $C_{\min}=-36$. Giá trị này đạt $x^2+5x=0\Leftrightarrow x=0$ hoặc $x=-5$

Tìm giá trị lớn nhất:

$D=5-8x-x^2=21-(x^2+8x+16)=21-(x+4)^2$

Vì $(x+4)^2\geq 0, \forall x\in\mathbb{R}$ nên $D=21-(x+4)^2\leq 21$

Vậy $D_{\max}=21$. Giá trị này đạt tại $(x+4)^2=0\Leftrightarrow x=-4$

$E=4x-x^2+1=5-(x^2-4x+4)=5-(x-2)^2\leq 5$

Vậy $E_{\max}=5$. Giá trị này đạt tại $(x-2)^2=0\Leftrightarrow x=2$