cho tam giác ABC,lấy D thuộc BC CM:2AD > AB + AC - BC

Những câu hỏi liên quan
cho tam giác ABC có điểm D thuộc BC
CM: 2AD>AB+AC-BC
Gọi MD là tia đối của tia AD sao cho : BD=DC
Xét tg ABD và tg DCM
có : AD=DM (DM đối vs AD)
BD=DC
D góc chung
Vậy tg ABD = tg DCM(cgc)
=> AB=MC
Nên :2AD>AC+MC+2DC
Suy ra : 2AD > AC+AB-BC
Vậy đpcm
Đúng 0
Bình luận (0)
Gọi MD là tia đối của tia AD sao cho : BD=DC
Xét tg ABD và tg DCM
có : AD=DM (DM đối vs AD)
BD=DC
D góc chung
Vậy tg ABD = tg DCM(cgc)
=> AB=MC
Nên :2AD>AC+MC+2DC
Suy ra : 2AD > AC+AB-BC
Vậy đpcm
OLM duyệt đi
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc C=40 độ, góc A vuông. Lấy D thuộc AC, E thuộc AB sao cho góc ADE = 20 độ và DE= DC. Cm: 2AD=BC
1.cho tam giác ABC có BC2AB. M là trung điểm của BC, D là trung điểm của BM.TRên tia AD lấy điểm E sao cho AE2AD. C/m: a, tam giác MAEtam giác MAC b, AC2AD2.cho tam giác ABC đều. D thuộc BC sao cho BC3BD.Vẽ DE vuông góc với BC(E thuộc AB) DF vuông góc với AC( F thuộc AC). C/m tam giác DEF đều.3. Cho tam giác ABC cân tại A.D thuộc AB. E thuộc AC sao cho ADAE. O là giao điểm của BE và CD. C/ma,BECD b, DE song song với BC
Đọc tiếp
1.cho tam giác ABC có BC=2AB. M là trung điểm của BC, D là trung điểm của BM.TRên tia AD lấy điểm E sao cho AE=2AD. C/m: a, tam giác MAE=tam giác MAC b, AC=2AD
2.cho tam giác ABC đều. D thuộc BC sao cho BC=3BD.Vẽ DE vuông góc với BC(E thuộc AB) DF vuông góc với AC( F thuộc AC). C/m tam giác DEF đều.
3. Cho tam giác ABC cân tại A.D thuộc AB. E thuộc AC sao cho AD=AE. O là giao điểm của BE và CD. C/m
a,BE=CD b, DE song song với BC
bai tinh chat tia phan giac cua mot goc
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, gọi D là trung điểm của BC, trên tia AD lấy điểm E sao cho D là trung điểm của AE. Chứng minh rằng:
1)Tam giác ABD=Tam giác ECD 2) EC vuông góc với AC
3) AB + AC > 2AD 4)BC=1/2AD
1: Xét ΔABD và ΔECD có
DA=DE
\(\widehat{ADB}=\widehat{EDC}\)
DB=DC
DO đó: ΔABD=ΔECD
2: Xét tứ giác ABEC có
D là trung điểm của AE
D là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: EC//AB
hay EC⊥AC
4:Ta có: ΔABC vuông tại A
mà AD là đường trung tuyến
nên AD=1/2BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, gọi D là trung điểm của BC, trên tia AD lấy điểm E sao cho D là trung điểm của AE. Chứng minh rằng:
1)Tam giác ABD=Tam giác ECD 2) EC vuông góc với AC
3) AB + AC > 2AD 4)BC=1/2AD
1: Xét ΔABD và ΔECD có
DA=DE
\(\widehat{ADB}=\widehat{EDC}\)
DB=DC
DO đó: ΔABD=ΔECD
2: Xét tứ giác ABEC có
D là trung điểm của AE
D là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: EC//AB
hay EC⊥AC
4:Ta có: ΔABC vuông tại A
mà AD là đường trung tuyến
nên AD=1/2BC
Đúng 1
Bình luận (0)
Cho tam giác ABC, đường phân giác AD (D thuộc BC), kẻ tia Dx song song với AB, tia Dx cắt AC tại E. Chứng minh tam giác 2AD<AB+BC+CA
2AD<AB+BC+CA
2AD bé thua AB+BC+CA
Do (hai góc ở vị trí so le trong)
Mà là đường phân giác nên
Từ 2 điều trên suy ra
cân đỉnh E (đpcm)

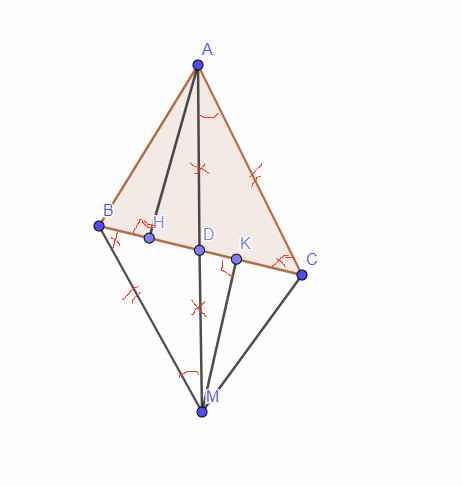
cho tam giác nhọn ABC (AB<AC).Gọi D là trung điểm của BC. Trên tia tới DA lấy diểm M sao cho DM=DA.
a)CM: tam giác ADC= tam giác MDB.
b)CM: AC= BM và AC//BM.
c) CM: tam giác ABM = tam giác MCA.
d) Kẻ AH vuông góc với BC, MK vuông góc với BC (H,K thuộc BC). CM: BK=DA.
a, Xét tam giác `ADC` và tam giác `MDB` có:
`DB=DC` `(g``t)`
\(\widehat{MDB}=\widehat{ADC}\) (2 góc đối đỉnh)
`DM=DA` `(g``t)`
`=>` Tam giác `ADC=` `MDB` `(c-``g-``c)`
`b,` vì tam giác `ADC=` Tam giác `MDB` (theo a)
`=> AC = BM` (2 cạnh tương ứng)
`=>` \(\widehat{ACD}=\widehat{MBD}\) (2 góc tương ứng)
mà 2 góc này nằm ở vị trí sole trong
`=> AC` //`BM` (d. hiệu nhận biết) (đpcm)
c, Vì Tam giác `ADC=` Tam giác `MDB` (theo a)
`=>`\(\widehat{DAC}=\widehat{DMB}\) (2 góc tương ứng)
Xét Tam giác `ABM` và Tam giác `MCA` có:
AM chung
\(\widehat{DAC}=\widehat{DMB}\) `(CMT)`
`BM = AC (CMT)`
`=>` Tam giác `ABM =` Tam giác `MCA (c-g-c)
d, *xl cậu câu này mình bí mất r:')
Đúng 4
Bình luận (1)
Bài 1: Cho tam giác ABC cân tại A. Lấy D, E thuộc BC sao cho BD = CF. CMR: tam giác ABC cân tại A.
Bài 2: Tam giác ABC cân tại A. Lấy M thuộc AB, N thuộc AC sao cho AM = AN.
a) CMR: MN//BC.
b) Cho CM cắt BN tại I. CMR: IB = IC.
Bài 3: Tam giác ABC cân tại A. Lấy M thuộc BC. Vẽ MK//AB (K thuộc AC). CMR: MK = KC.
cho tam giác ABC vuông tại A có AB=3CM , AC= 4 CM , BC=5cm
a) so sánh các góc của tam giác ABC
b) vẽ tia phân giác BD của tam giác ABC ( D thuộc AC ) trên cạnh BC lấy điểm E sao cho AB=BE. CM tâm giác ABD= tam giác EBD
c) CM: DB là phân giác của góc ADE
d) CM: DE vuông góc BC
a: AB<AC<BC
=>góc C<gócB<góc A
b: Xét ΔABD và ΔEBD có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
c,d: ΔBAD=ΔBED
=>góc ADB=góc EDB và góc BAD=góc BED=90 độ
=>DB là phân giác của góc ADE và DE vuông góc BC
Đúng 0
Bình luận (0)
















