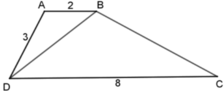
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng là tam giác ABD đồng dạng với tam giác BDC
a) cmr AB song song với CD
b) Tính các độ dài BD, BC biết AB=2cm , AD=3cm , CD=8cm
Giup minh voi
Những câu hỏi liên quan
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD và ΔBDC. Tính các độ dài BD, BC biết AB = 2cm, AD = 3cm, CD = 8cm.
A. BD = 5cm, BC = 6cm
B. BD = 6cm, BC = 4cm
C. BD = 6cm, BC = 6cm
D. BD = 4cm, BC = 6cm
Vì ΔABD ⁓ ΔBDC nên A B B D = B D D C = A D B C , tức là 2 B D = B D 8 = 3 B C
Ta có B D 2 = 2.8 = 16 nên BD = 4 cm
Suy ra BC = 8.3 4 = 6 cm
Vậy BD = 4cm, BC = 6cm
Đáp án: D
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có đg chéo BD chia tứ giác thành 2 tam giác đồng dạng. Tam giác ABD và Tam giác BDC
a, CMR. AB//CD
b, Tính BD,NC biết AB =2 cm, AD=3cm,CD=8cm.
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD ⁓ ΔBDC. Cho AB = 2cm, AD = 3cm, CD = 8cm. Tính đọ dài cạnh còn lại của tứ giác ABCD.
A. BC = 6cm
B. BC = 4cm
C. BC = 5cm
D. BC = 3cm
Vì ΔABD ⁓ ΔBDC nên A B B D = B D D C = A D B C , tức là 2 B D = B D 8 = 3 B C
Ta có B D 2 = 2.8 = 16 nên BD = 4 cm
Suy ra BC = 8.3 4 = 6 cm
Vậy BD = 4cm, BC = 6cm
Đáp án: A
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có đg chéo BD chia tứ giác thành 2 tam giác đồng dạng. Tam giác ABD và Tam giác BDCa, CMR. AB//CDb, Tính BD,NC biết AB =2 cm, AD=3cm,CD=8cm.
Bài làm
a) Vì tam giác ABD ~ tam giác CDB ( gt )
=> \(\widehat{ABD}=\widehat{BDC}\)( hai góc tương ứng )
Mà hai góc này ở vị trí so le trong
=> AB // CD
b) Vì tam giác ABD ~ tam giác CDB ( gt )
=> \(\frac{AB}{CD}=\frac{AD}{BC}=\frac{BD}{BD}\)
hay \(\frac{2}{8}=\frac{3}{BC}=\frac{BD}{BD}\)
=> BC = 8 . 3 : 2 = 12 ( cm )
Cho tứ giác abcd có đường chéo bd chia tứ giác đó thành 2 tam giác đồng dạng abd và bdc.
A, CMR ab//dc
B, Tính bd, bc biết ab= 2 cm, da=3 cm, cd=8 cm
Mong mọi người giúp đỡ và vẽ hộ hình
Cho tứ giác ABCDcos AB = 3cm, BC = 10cm, CD = 12cm, AD = 5cm và đường chéo BD = 6cm.
a) Chứng minh tam giác ABD đồng dạng với tam giác BDC
b) Chứng minh tứ giác ABCD là hình thang
c) Hai đường chéo AC và BD cắt nhau tại O. Tính DO
Cho tứ giác ABCD có AB = 3cm ; BC = 10cm ; CD = 12cm ; AD = 5cm, đường chéo BD = 6cm. Chứng minh rằng
a) Tam giác ABD đồng dạng với tam giác BCD
b) ABCD là hình thang
a: Xét ΔABD và ΔBDC có
AB/BD=BD/CD=AD/BC
=>ΔABD đồng dạng với ΔBDC
b: ΔABD đồng dạng với ΔBDC
=>góc ABD=góc BDC
=>AB//CD
Đúng 0
Bình luận (0)
Tứ giác ABCD có AB = 3cm, BC = 10cm, CD = 12cm, AD = 5cm,
đường chéo BD = 6cm.
Chứng minh rằng :
a) Tam giác ABD đồng dạng tam giác BDC rồi suy ra BD2=AB.CD
b) Tứ giác ABCD là hình thang.
Tứ giác ABCD có AB = 4cm, BC = 20cm, CD = 25cm. DA = 8cm, đường chéo BD = 10cm.
a) Nếu cách vẽ tứ giác ABCD có kích thước đã cho ở trên.
b) Các tam giác ABD và BDC có đồng dạng với nhau không? Vì sao?
c) Chứng minh rằng AB // CD.
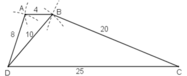
a) Cách vẽ:
- Vẽ ΔBDC:
+ Vẽ DC = 25cm
+ Vẽ cung tròn tâm D có bán kính = 10cm và cung tròn tâm C có bán kính = 20cm. Giao điểm của hai cung tròn là điểm B.
Nối DB và BC.
- Vẽ điểm A: Vẽ cung tròn tâm B có bán kính = 4cm và cung tròn tâm D có bán kính = 8cm. Giao điểm của hai cung tròn này là điểm A.
Nối DA và BA.
Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.
Đúng 0
Bình luận (0)