Cho hàm số FX có đạo hàm liên tục trên đoạn [0;1] bằng mãn f (1) = 1 và (f'(x))²+4(6x²-1).f(x)=40x⁶-44x⁴+32x²-4,Tích phân cân từ 0 đến 1 của xf(x)dx bằng
A.-13/15
B.5/12
C.13/15
B.-5/12
Những câu hỏi liên quan
Cho các mệnh đề sau:1. Nếu hàm số
y
f
x
liên tục, có đạo hàm tới cấp hai trên
a
;
b
,
x
0
∈
a
;
b
và
f
x...
Đọc tiếp
Cho các mệnh đề sau:
1. Nếu hàm số y = f x liên tục, có đạo hàm tới cấp hai trên a ; b , x 0 ∈ a ; b và f ' x 0 = 0 f ' ' x 0 ≠ 0 thì x0 là một điểm cực trị của hàm số.
2. Nếu hàm số y = f x xác định trên a ; b thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
3. Nếu hàm số y = f x liên tục trên a ; b thì hàm số có đạo hàm tại mọi x thuộc [a;b].
4. Nếu hàm số y = f x có đạo hàm trên a ; b thì hàm số có nguyên hàm trên a ; b
Số mệnh đề đúng là:
A. 2
B. 1
C. 3
D. 4
Đáp án A.
Mệnh đề 3 sai ví dụ hàm số y=|x| liên tục tại x = 0 nhưng không có đạo hàm tại điểm đó.
Mệnh đề 4 đúng vì nếu hàm số y=f(x) có đạo hàm trên [a;b] thì hàm số liên tục trên [a;b] do đó hàm số có nguyên hàm trên [a;b]
Đúng 0
Bình luận (0)
Cho hàm số
f
x
có đạo hàm và liên tục trên đoạn
4
;
8
và
f
x
≠
0
∀
x
∈
4
;
8
.
Biết rằng
∫
4
8
f...
Đọc tiếp
Cho hàm số f x có đạo hàm và liên tục trên đoạn 4 ; 8 và f x ≠ 0 ∀ x ∈ 4 ; 8 . Biết rằng ∫ 4 8 f ' x 2 f x 4 d x = 1 và f 4 = 1 4 , f 8 = 1 2 . Tính f 6 .
A. 5 8 .
B. 2 3 .
C. 3 8 .
D. 1 3 .
Đáp án D.
Ta có:
∫ 4 8 f ' x f x 2 d x = ∫ 4 8 f x − 2 d f x = f x − 1 − 1 4 8 = − 1 f 8 + 1 f 4 = − 2 + 4 = 2.
Gọi k là 1 hằng số thực. Xét
∫ 4 8 f ' x f 2 x + k 2 d x = ∫ 4 8 f ' x 2 f x 4 d x + 2 k ∫ 4 8 f ' x f 2 x d x + k 2 ∫ 4 8 d x = 1 + 2 k . k + 4 k 2 = 2 k + 1 2 .
Chọn k = − 1 2 , ta có ∫ 4 8 f ' x f 2 x − 1 2 2 d x = 0 , mà f ' x f 2 x − 1 2 2 ≥ 0 nên f ' x f 2 x − 1 2 2 = 0 ⇔ f ' x f 2 x = 1 2
⇒ ∫ f ' x f 2 x d x = x 2 + C ⇒ − 1 f x = x 2 + C .
Với x = 4 , ta có
− 1 f 4 = 2 + C ⇔ − 4 = 2 + C ⇔ C = − 6.
Do đó: f x = − 1 x 2 − 6 = 2 12 − x . Do đó f 6 = 2 12 − 6 = 2 6 = 1 3 .
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
có đạo hàm liên tục trên đoạn
0
,
1
và
f
0
+
f
1
0
. Biết
∫
0
1
f
2
x
d
x
1
2
;...
Đọc tiếp
Cho hàm số y = f x có đạo hàm liên tục trên đoạn 0 , 1 và f 0 + f 1 = 0 . Biết
∫ 0 1 f 2 x d x = 1 2 ; ∫ 0 1 f ' x cos π x d x = π 2 . Tính ∫ 0 1 f x d x
A. π
B. 3 π 2
C. 2 π
D. 1 π
Cho hàm số
f
x
có đạo hàm liên tục trên đoạn
0
;
1
thỏa mãn
f
1
0
,
∫
0
1
f
x
2
d
x
7
và
∫...
Đọc tiếp
Cho hàm số f x có đạo hàm liên tục trên đoạn 0 ; 1 thỏa mãn f 1 = 0 , ∫ 0 1 f ' x 2 d x = 7 và ∫ 0 1 x 2 f x d x = 1 3 . Tích phân ∫ 0 1 f x d x bằng
A. 7 5 .
B. 1
C. 7 4 .
D. 4
Đáp án A.
Đặt u = f x d v = 3 x 2 d x ⇒ d u = f ' x d x v = x 3 ,
khi đó ∫ 0 1 3 x 2 f x d x = x 3 f x 1 0 − ∫ 0 1 x 3 f ' x d x .
⇒ 1 = f 1 − ∫ 0 1 x 3 f ' x d x ⇒ ∫ 0 1 x 3 f ' x d x = − 1 ⇔ ∫ 0 1 14 x 3 f ' x d x = − 7.
Mà ∫ 0 1 49 x 6 d x = 7
s u y r a ∫ 0 1 f ' x 2 d x + ∫ 0 1 7 ∫ 0 1 x 3 f ' x d x + ∫ 0 1 49 x 6 d x = 0 ⇔ ∫ 0 1 f ' x + 7 x 3 2 d x = 0.
Vậy
f ' x + 7 x 3 = 0 ⇒ 0 ⇒ f x = − 7 4 x 4 + C
Đúng 0
Bình luận (0)
Cho hàm số
f
x
có đạo hàm liên tục trên đoạn
0
;
1
thỏa mãn
f
1
0
và
∫
0
1
f
x
2
d
x
∫
0...
Đọc tiếp
Cho hàm số f x có đạo hàm liên tục trên đoạn 0 ; 1 thỏa mãn f 1 = 0 và
∫ 0 1 f ' x 2 d x = ∫ 0 1 x + 1 e x d x = e 2 − 1 4 .
Tính tích phân I = ∫ 0 1 f x d x .
A. I = 2 − e
B. I = e − 2
C. I = e 2
D. I = e − 1 2
Cho hàm số
y
f
x
có đạo hàm liên tục trên đoạn
0
;
1
và thỏa mãn
f
0
0
. Biết
∫
0
1
f
2
x
d
x
9
2
v
à...
Đọc tiếp
Cho hàm số y = f x có đạo hàm liên tục trên đoạn 0 ; 1 và thỏa mãn f 0 = 0 . Biết ∫ 0 1 f 2 x d x = 9 2 v à ∫ 0 1 f ' x cos π x 2 d x = 3 π 4 . Tích phân ∫ 0 1 f x d x b ằ n g
A. 6 π
B. 2 π
C. 4 π
D. 1 π
Đặt
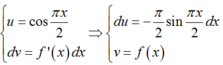
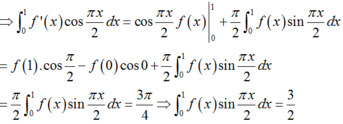
Xét tích phân
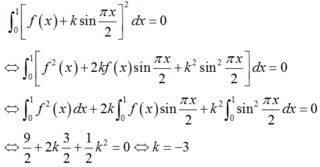
Khi đó ta có
∫ 0 1 f x = 3 sin π x 2 2 d x = 0 ⇔ f x - 3 sin π x 2 = 0 ⇔ f x = 3 sin π x 2
Vậy
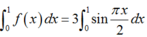
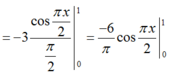
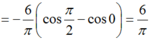
Chọn A.
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
có đạo hàm liên tục trên đoạn
0
;
π
4
và
f
π
4
0.
Biết rằng ta có điều kiện
∫
0
π
4
f
2
x...
Đọc tiếp
Cho hàm số y = f x có đạo hàm liên tục trên đoạn 0 ; π 4 và f π 4 = 0. Biết rằng ta có điều kiện ∫ 0 π 4 f 2 x d x = π 8 ; ∫ 0 π 4 f ' x sin 2 x d x = − π 4 . Tính tích phân I = ∫ 0 π 8 f 2 x d x .
A. I = 1 2
B. I = 1 4
C. I = 2
D. I = 1
Đáp án B.
Ta có ∫ 0 π 4 f ' x sin 2 x d x
Đặt u = sin 2 x d v = f ' x ⇒ d u = 2 cos 2 xdx v = f x suy ra
∫ 0 π 4 f ' x sin 2 x d x = sin 2 x f x π 4 0 − ∫ 0 π 4 2 cos 2 x . f x d x
⇒ − 2 ∫ 0 π 4 c o s 2 x . f x d x = − π 4 ⇒ ∫ 0 π 4 c o s 2 x . f x d x = π 8
Lại có: ∫ 0 π 4 c o s 2 2 x . f x d x = π 8 ⇒ ∫ 0 π 4 f x − c o s 2 x 2 d x = 0 ⇒ f x = c o s 2 x
Do đó ∫ 0 π 8 f 2 x d x = ∫ 0 π 8 c o s 4 x d x = sin 4 x 4 π 8 0 = 1 4 .
Đúng 0
Bình luận (0)
Cho hàm số
f
x
có đạo hàm cấp hai
f
x
liên tục trên đoạn [0;1] thoả mãn
f
1
f
(
0
)
1
,
f
(
0
)
2018
Mệnh đề nào dưới đây đúng ? A.
∫
0...
Đọc tiếp
Cho hàm số f x có đạo hàm cấp hai f ' ' x liên tục trên đoạn [0;1] thoả mãn f 1 = f ( 0 ) = 1 , f ' ( 0 ) = 2018 Mệnh đề nào dưới đây đúng ?
A. ∫ 0 1 f ' ' ( x ) 1 - x d x = - 2018 .
B. ∫ 0 1 f ' ' ( x ) 1 - x d x = 1 .
C. ∫ 0 1 f ' ' ( x ) 1 - x d x = 2018 .
D. ∫ 0 1 f ' ' ( x ) 1 - x d x = - 1 .
Cho hàm số
y
f
x
có đạo hàm liên tục trên đoạn
0
;
1
và
f
0
+
f
1
0.
Biết rằng tích phân
∫
0
1
f
2
x
d
x
1
2...
Đọc tiếp
Cho hàm số y = f x có đạo hàm liên tục trên đoạn 0 ; 1 và f 0 + f 1 = 0. Biết rằng tích phân ∫ 0 1 f 2 x d x = 1 2 , ∫ 0 1 f ' x . c o s π x d x = π 2 . Tính tích phân ∫ 0 1 f x d x ?
A. 3 π 2 .
B. 2 π .
C. π .
D. 1 π .
Đáp án B.
Ta có ∫ 0 1 f ' x . c o s π x d x
= ∫ 0 1 c o s π x d f x = f x . c o s π x 0 1 − ∫ 0 1 f x . c o s π x ' d x
= − f 1 + f 0 + π ∫ 0 1 f x . sin π x d x = π 2 ⇒ ∫ 0 1 f x . sin π x d x = 1 2 .
Xét ∫ 0 1 f x + k . sin π x 2 d x = 0
⇔ ∫ 0 1 f 2 x d x + 2 k . ∫ 0 1 f x . sin π x d x + k 2 . ∫ 0 1 sin 2 π x d x = 0
⇔ 1 2 k 2 + 2 k . 1 2 + 1 2 = 0 ⇔ k + 1 2 = 0 ⇔ k = − 1.
Suy ra ∫ 0 1 f x − sin π x 2 d x = 0.
Vậy f x = sin π x ⇒ ∫ 0 1 f x d x = ∫ 0 1 sin π x d x = 2 π .
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
có đạo hàm liên tục trên đoạn
-
2
;
1
thỏa mãn
f
0
1
và
f...
Đọc tiếp
Cho hàm số y = f x có đạo hàm liên tục trên đoạn - 2 ; 1 thỏa mãn f 0 = 1 và f x 2 . f ' x = 3 x 2 + 4 x + 2 . Giá trị lớn nhất của hàm số y = f x trên đoạn - 2 ; 1 là:
A. 2 16 3
B. 18 3
C. 16 3
D. 2 18 3
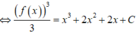
Xét hàm f x = 3 x 2 + 6 x 2 + 6 x + 1 3 trên - 2 ; 1
Ta có
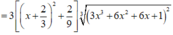
Nhận thấy f ' x > 0 , ∀ x ∈ ℝ
⇒ Hàm số đồng biến trên - 2 ; 1
Suy ra m a x [ - 2 , 1 ] f x = f 1 = 16 3
Chọn C
Đúng 0
Bình luận (0)