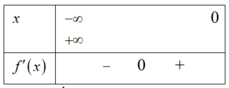
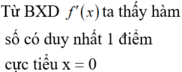Tìm cực trị của f(x,y)= 2x4 + y2 -2x2 -2y

Những câu hỏi liên quan
Cho hàm số
y
f
x
có đạo hàm
f
x
x
−
1
x
2
−
2
x
4
−
...
Đọc tiếp
Cho hàm số y = f x có đạo hàm f ' x = x − 1 x 2 − 2 x 4 − 4 . Số điểm cực trị của hàm số y = f x
A. 2
B. 3
C. 4
D. 1
Đáp án A
Vận tốc của vật có PT là:
v = s ' = 3 t 2 − 6 t + 6 = 3 t − 1 2 + 3 ≥ 3
Do đó vận tốc nhỏ nhất của vật là: v min = 3 m / s .
Đúng 0
Bình luận (0)
Tìm tất cả các nghiệm nguyên của phương trình x5-2x4+2x2-(y2+3)x+2y2-2=0
\(x^5\) - 2\(x^4\) - (y2 + 3)\(x\) + 2y2 - 2 = 0
(\(x^5\) - 2\(x^4\))- (y2 + 3)\(x\) + 2.(y2 + 3) - 8 = 0
\(x^4\).(\(x\) - 2) - (y2 + 3).(\(x\) - 2) - 8 = 0
(\(x\) - 2).(\(x^4\) - y2 - 3) = 8
8 = 23; Ư(8) = {-8; - 4; -2; - 1; 1; 2; 4; 8}
Lập bảng ta có:
| \(x-2\) | -8 | -4 | -2 | -1 | 1 | 2 | 4 | 8 |
| \(x\) | -6 | -2 | 0 | 1 | 3 | 4 | 6 | 10 |
| \(x^4\) - y2 - 3 | -1 | -2 | -4 | -8 | 8 | 4 | 2 | 1 |
| y | \(\pm\)\(\sqrt{1294}\) | \(\pm\)\(15\) | \(\pm\)1 | \(\pm\)\(\sqrt{6}\) | y2 = -10 (ktm) | \(\pm\)\(\sqrt{249}\) | \(\pm\)\(\sqrt{1291}\) | \(\pm\)\(\sqrt{9996}\) |
vì \(x\); y nguyên nên theo bảng trên ta có các cặp \(x\); y thỏa mãn đề bài là:
(\(x\); y) = (0; -1;); (0; 1)
Đúng 0
Bình luận (0)
Cho hệ phương trình
x
+
y
m
-
2
x
2
+
y
2
+...
Đọc tiếp
Cho hệ phương trình x + y = m - 2 x 2 + y 2 + 2 x + 2 y = - m 2 + 4 (trong đó m là tham số). Tìm tất cả các giá trị của m để hệ có nghiệm
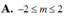
![]()
![]()
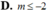
![]()
Cho số phức
z
x
+
y
i
(
x
,
y
∈
R
)
thỏa mãn
z
-
2
+
i
z
+
2
+
5
i
và biểu thức
H
x...
Đọc tiếp
Cho số phức z = x + y i ( x , y ∈ R ) thỏa mãn z - 2 + i = z + 2 + 5 i và biểu thức H = x 2 + y 2 - 3 y + 1 x 2 + y 2 + 2 x - 2 y + 2 x 2 + y 2 - 2 x - 4 y + 5 đạt giá trị nhỏ nhất. Giá trị của 2x + y bằng
A. -6
B. - 6 + 5
C. - 3 - 5
D. - 6 - 5
tìm cực trị của f= x+2y+2z, với điều kiện x^2+y^2+z^2=9
Tìm x,y là số nguyên :
c) 2x2+y2-2xy+2y-6x=5
e) x2+y2=9x+13y-20
Cho F(x)
x
4
-
2
x
2
+
1
là một nguyên hàm của hàm số
f
(
x
)
-
4
x
. Hàm số
y
f
(
x
)
có tất cả bao nhiêu điểm cực trị?
Đọc tiếp
Cho F(x)= x 4 - 2 x 2 + 1 là một nguyên hàm của hàm số f ' ( x ) - 4 x . Hàm số y = f ( x ) có tất cả bao nhiêu điểm cực trị?
![]()
![]()
![]()
![]()
tìm cặp số nguyên (x;y) thỏa mãn: 2x2+y2+2xy-6x-2y=8
Lời giải:
$2x^2+y^2+2xy-6x-2y=8$
$\Leftrightarrow (x^2+y^2+2xy)+x^2-6x-2y=8$
$\Leftrightarrow (x+y)^2-2(x+y)+x^2-4x=8$
$\Leftrightarrow (x+y)^2-2(x+y)+1+(x^2-4x+4)=13$
$\Leftrightarrow (x+y-1)^2+(x-2)^2=13$
$\Rightarrow (x-2)^2=13-(x+y-1)^2\leq 13$
Mà $(x-2)^2$ là scp với mọi $x$ nguyên nên $(x-2)^2\in\left\{0; 1; 4; 9\right\}$
Nếu $(x-2)^2=0\Rightarrow (x+y-1)^2=13-(x-2)^2=13$ (không là scp - loại)
Nếu $(x-2)^2=1\Rightarrow (x+y-1)^2=12$ (không là scp - loại)
Nếu $(x-2)^2=4\Rightarrow (x+y-1)^2=9$
$\Rightarrow x-2=\pm 2$ và $x+y-1=\pm 3$
TH1: $x-2=2; x+y-1=3\Rightarrow x=4; y=0$
TH2: $x-2=2; x+y-1=-3\Rightarrow x=4; y=-6$
TH3: $x-2=-2; x+y-1=3\Rightarrow x=0; y=4$
TH4: $x-2=-2; x+y-1=-3\Rightarrow x=0; y=-2$
Nếu $(x-2)^=9\Rightarrow (x+y-1)^2=4$ (bạn cũng làm tương tự trên)
Đúng 2
Bình luận (2)
Tìm điểm cực trị M của đồ thị hàm số
y
x
+
2
x
2
+
1
Đọc tiếp
Tìm điểm cực trị M của đồ thị hàm số y = x + 2 x 2 + 1
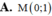
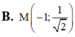
![]()
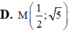
Cho hàm số
y
−
x
4
+
2
x
2
+
3
có giá trị cực tiểu lần lượt là
y
1
,
y
2
.
Khi đó
y
1
+
y
2
bằng A. 7 B. 1 C. .3 D. -1
Đọc tiếp
Cho hàm số y = − x 4 + 2 x 2 + 3 có giá trị cực tiểu lần lượt là y 1 , y 2 . Khi đó y 1 + y 2 bằng
A. 7
B. 1
C. .3
D. -1
Chọn A.

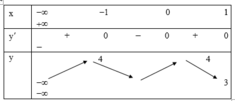
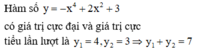
Chú ý: Cần phân biệt điểm cực đại và giá trị cực đại cũng như điểm cực tiểu và giá trị cực tiểu của hàm số.
Đúng 0
Bình luận (0)