Câu 7. Một viên vi thả lăn không vận tốc ban đầu trên một mặt phẳng nghiêng, chuyển động thẳng nhanh dần đều, sau 2 giây đi được 20m.
a/ Tính vận tốc và quãng đường bi được trong 4 giây.
b/ Tính quãng đường bi được trong giây thứ 4.
1 viên bi được thả cho lăn không vận tốc đầu trên 1 mặt phẳng nghiêng ,chuyển động thẳng nhanh dần đều ,sau 4s đi được 80cm.
a,tính vận tốc và quãng đường đi được sau 6s
b,tính quãng đường viên bi đi được trong giây thứ 6
giúp em vs em cần lúc 5h em cần gấp
a, Ta có: \(v^2-v_0^2=2aS\Leftrightarrow4^2-0=2.a.80.10^{-2}\)
\(\Leftrightarrow a=10\left(\dfrac{m}{s^2}\right)\)
Vận tốc của vật sau 6s là: v=v0+at=10.6=60(m/s)
Quãng đường vật đi được sau 6s là:
\(s=\dfrac{v^2-v_0^2}{2a}=\dfrac{60^2-0}{2.10}=180\left(m\right)\)
b, Quãng đường viên bi đi được trong giây thứ 6 là:
x=v0t+\(\dfrac{1}{2}at^2\)=\(\dfrac{1}{2}.10.6^2=180\left(m\right)\)
Bạn tham khảo nha
Bài 2: (Biến đổi đều) Một viên bi được thả lăn không vận tốc ban đầu trên mặt
phẳng nghiêng chuyển động nhanh dần đều sau 4s thì đi được quãng đường
80cm.
a. Gia tốc của viên bi
b. Vận tốc của bi sau 5s là bao nhiêu?
c. Quãng đường đi được sau 5s là bao nhiêu?
giúp em với ạ em cần gấp, lúc 6h có bài cho em liền nhé, em cần gấp lắm ạ. Em cảm ơn nhiều ạ
a) Gia tốc viên bi: \(S=\dfrac{1}{2}at^2\Rightarrow a=\dfrac{2\cdot0,8}{4^2}=0,1\)m/s2
b) Vận tốc của bi sau 5s: \(v=at=0,1\cdot5=0,5s\)
c) Quãng đường vật đi được sau 5s:
\(S=\dfrac{1}{2}at^2=\dfrac{1}{2}\cdot0,1\cdot5^2=1,25m\)
Một viên bi chuyển động thẳng nhanh dần đều với gia tốc a, không vận tốc đầu trên máng nghiêng và trong giây thứ năm nó đi được quãng đường bằng 36 cm. Quãng đường viên bi đi được sau 5 giây kể từ khi nó bắt đầu chuyển động là s5. Độ lớn của s5/a bằng
A. 8,6 s2.
B. 12,5 s2
C. 10 s2
D. 75 s2
Một viên bi chuyển động thẳng nhanh dần đều với gia tốc a, không vận tốc đầu trên máng nghiêng và trong giây thứ năm nó đi được quãng đường bằng 36 cm. Quãng đường viên bi đi được sau 5 giây kể từ khi nó bắt đầu chuyển động là s5. Độ lớn của s5/a bằng
A. 8,6 s2.
B. 12,5 s2
C. 10 s2
D. 75 s2
Một viên bi lăn từ đỉnh một mặt phẳng nghiêng xuống với gia tốc 0 , 45 m / s 2
a)Tính vận tốc của bi sau 2 giây kể từ lúc chuyển động.
b) Sau bao lâu từ lúc thả lăn, viên bi đạt vận tốc 6,3m/s. Tính quãng đường bi đi được từ lúc thả đến khi bi đat vận tốc 6,3m/s (nếu mặt nghiêng đủ dài).
Chọn chiều dương là chiều chuyển động.
a) Vận tốc tại t = 2 s s: v t = a t = 0 , 45.2 = 0 , 9 m/s.
b) Thời gian: t = v 1 a = 6 , 3 0 , 45 = 14 s.
Từ công thức v 2 − v 0 2 = 2 a s ⇒ quãng đường s = 6 , 3 2 0 , 45 = 44 , 1 m.
một viên bi chuyển động thẳng nhanh dần đều không vận tốc đầu trên máng nghiêng và trong giây thứ năm nó đi được quãng đường 36cm.
a) Tính gia tốc của viên bi chuyển động trên máng nghiêng.
b) Tính quãng đường viên bi đi được sau 5s kể từ khi nó bắt đầu chuyển động.![]()
Chọn chiều dương là chiều chuyển động của bi
a) Từ công thức tính quãng đường: \(s=\frac{at^2}{2}\)
Quãng đường đi được trong 4s đầu tiên: \(s_4=\frac{\text{a4}^2}{2}=8a\)
Quãng đường đi được trong 5s đầu tiên
\(s_5=\frac{\text{a5}^2}{2}=12,5a\)
Quãng đường đi được trong giây thứ 5:
\(\Delta s=s_5-s_4=12,5a-8a=4,5a\)
Ta có: \(\Delta s=0,36m\Rightarrow a=\frac{0,36}{4,5}=0,08\) m/s2
b) Với a = 0,08m/s2 có 5s = 12,5a = 12,5 . 0,08 = 1m
Từ công thức v = at => Vận tốc ở cuổi quãng đường v = 0,8.5 = 0,4 m/s
một xe chuyển động thẳng nhanh dần đều với vận tốc ban đầu Vo=24km/h. Trong giây thứ 6 kể từ lúc bắt đầu chuyển động nhanh dần xe đi được quãng đường 18m. Tính gia tốc của xe và quãng đường xe đi được sau 15s và trong giây thứ 12
Một viên bi được thả lăn không vận tốc ban đầu trên một mặt phẳng nghiêng, chuyển động thẳng nhanh dần đều sau 4s đi được 80cm
a) Tính vận tốc và quãng đường đi được sau 6s
b) Tính quãng đường viên bi đ được trong giây thứ 6
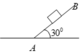
Một viên bi khối lượng m chuyển động ngang không ma sát với vận tốc 2 m/s rồi đi lên mặt phẳng nghiêng góc nghiêng 30o.
a.Tính quãng đường s mà viên bi đi được trên mặt phẳng nghiêng
b. Ở độ cao nào thì vận tốc của viên bi giảm còn một nửa.
c. Khi vật chuyển động được quãng đường là 0,2 m lên mặt phẳng nghiêng thì vật có vận tốc bao nhiêu.
Chọn mốc thế năng tại A, giả sử lên đén B vật dừng lại
a. Theo định luật bảo toàn cơ năng
W A = W B ⇒ 1 2 m v A 2 = m g z B ⇒ z B = v A 2 2 g ⇒ z = 2 2 2.10 = 0 , 2 ( m ) ⇒ sin 30 0 = z B s ⇒ s = z B sin 30 0 = 0 , 2 1 2 ⇒ s = 0 , 4 ( m )
b. Gọi C là vị trí mà vận tốc giảm đi một nửa tức là còn 1 m/s
Theo định luật bảo toàn cơ năng
W A = W B ⇒ 1 2 m v A 2 = m g z c + 1 2 m v C 2 ⇒ z C = 1 2 g ( v A 2 − v C 2 ) ⇒ z C = 1 2.10 ( 2 2 − 1 2 ) = 0 , 15 ( m )
Vật chuyển động được một quãng đường
s = z C sin 30 0 = 0 , 3 ( m )
c. Khi vật đi được quãng đường 0,2m thì vật có độ cao
z D = s / . sin 30 0 = 0 , 2. 1 2 = 0 , 1 ( m )
Theo định luật bảo toàn cơ năng
W A = W D ⇒ 1 2 m v A 2 = m g z D + 1 2 m v D 2 ⇒ v D = v A 2 − 2 g z D ⇒ v D = 2 2 − 2.10.0 , 1 = 2 ( m / s )