Cho tam giác ABC, đường phân giác AD (D thuộc BC), kẻ tia Dx song song với AB, tia Dx cắt AC tại E. Chứng minh tam giác 2AD<AB+BC+CA

Những câu hỏi liên quan
Bài 4: Cho tam giác ABC, đường phân giác AD (D thuộc BC), kẻ tia Dx song song với AB, tia Dx cắt AC tại E. Chứng minh tam giác ADE là tam giác cân
cho tam giác ABC, tia phân giác ABC cắt AC tại D. Qua D kẻ Dx song song và AB, Dx cắt BC tại M, gọi My là tia phân giác góc DMC, Bz là tia phân giác ngoài của B. Chứng minh rằng Bz vuông góc My
1. Cho tam giác AB, tia phân giác của góc B cắt AC tại D. Qua D kẻ tia Dx song song với AB, Dx cắt BC tại M. kẻ tia My là phân giác của góc DMC, Bz là tia phân giác của góc ngoài tại đỉnh B. Chứng minh: Bz vuông góc My.2. Cho tam giác ABC vuông tại A, đường cao AH, có AB 12cm, BC 15cm. a, Tính AC, AH. b, So sánh HB và HC. c, Trên đoạn thẳng HC lấy điểm M bất kỳ. Qua M kẻ đường thẳng song song với AC cắt AH tại D. Chứng minh: BD vuông góc AM
Đọc tiếp
1. Cho tam giác AB, tia phân giác của góc B cắt AC tại D. Qua D kẻ tia Dx song song với AB, Dx cắt BC tại M. kẻ tia My là phân giác của góc DMC, Bz là tia phân giác của góc ngoài tại đỉnh B. Chứng minh: Bz vuông góc My.
2. Cho tam giác ABC vuông tại A, đường cao AH, có AB = 12cm, BC = 15cm.
a, Tính AC, AH.
b, So sánh HB và HC.
c, Trên đoạn thẳng HC lấy điểm M bất kỳ. Qua M kẻ đường thẳng song song với AC cắt AH tại D. Chứng minh: BD vuông góc AM
Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.
Đúng 0
Bình luận (0)
cho tam giác ABC, tia phân giác ABC cắt cạnh Ac tại điểm D, qua điểm D kẻ tia Dx song song với AB, tia Dx cắt BC tại điểm M, gọi tia My là tia phân giác của góc DMC; Bz là tia phân giác cung2 góc ngoài đỉnh B của Tam giác ABC
Chứng mính Bz vuông với My
cho tam giác ABC đường phân giác AD (D thuộc BC) kẻ tia DX song song vói AB, tia Dx cắt AC tại E chứng minh tam giác DEA cân
Vì DE//AB => \(\widehat{BAD}\) = \(\widehat{ADE}\) (so le trong ) (1)
Vì AD là tia phân giác \(\widehat{BAC}\)
=> \(\widehat{BAD}\) = \(\widehat{DAC}\) = \(\frac{1}{2}\) \(\widehat{BAC}\) (2)
Từ(1) và (2) => \(\widehat{ADE}\) = \(\widehat{DAC}\) hay \(\widehat{ADE}\) = \(\widehat{DAE}\)
Trong \(\Delta\)AED có \(\widehat{ADE}\) = \(\widehat{DAE}\) nên \(\Delta\)AED là tam giác cân tại E
Đúng 0
Bình luận (1)
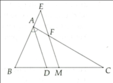
Cho tam giác ABC (AB < AC), đường phân giác AD của B A C ^ (với D ∈ B C ). Từ trung điểm M của BC, kẻ một đường thẳng song song với AD, cắt AC tại F và cắt tia đối của tia AB tại E. Chứng minh BE = CF
Cho tam giác ABC có AB lớn hơn AC tia phân giác của góc A cắt BC tại D qua B kẻ đường thẳng vuông góc với AC cắt AC tại E
a Chứng minh AB =AE
b qua qua e kẻ đường thẳng song song với BC cắt AD tại F kẻ đường hai đường thẳng song song với BC tại K
Gọi Bx là tia đối của tia BA. Lấy E trên AC sao cho AB = AE
Xét tam giác BAD=EAD c-g-c => BD = DE và DEC = CBx
Trong tam giác ABC, BAC + ABC + ACB = 180 => ACB = 180 - BAC - ABC => ACB < 180 - ABC
Ta có DBx + ABC = 180 (hai góc kề bù) => DBx = 180 - ABC
=>ACB < DBx => ACB < DEC => Trong tam giác DEC, DC > DE (Quan hệ giữa góc và cạnh)
Vậy BD < DC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB < AC kẻ đường cao AH. Trên tia đối của tia AH lấy điểm D sao cho HD = HA a) Chứng minh tam giác ABH = tam giác DBH b) Chứng minh CB là tia phân giác góc ACD c) Qua A kẻ đường thẳng song song với BD, cắt cạnh BC tại E. Chứng minh DE // AB d) Đường thẳng AE cắt đường thẳng CD tại K. Chứng minh HK = 1/2AD
lam ho mk cau d
help me
Cho tam giác ABC kẻ EF song song với BC (E thuộc AB, F thuộc AC) sao cho AE =CF. Qua E kẻ 1 đường thẳng song song với AC cắt BC tại D a, chứng minh AD là tia phân giác của góc A b, hãy dựng 1 đường thẳng MN song song với (M thuộc AB, N thuộc AC) sao cho BM =AN c, tam giác ABC phải có điều kiện gì để tứ giác MNDB là hình thoi