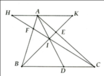
Cho \(\Delta\)ABC có trọng tâm G. Đường thẳng d đi qua G cắt tia BC ở \(A_1\) ( \(A_1\) nằm ngoài cạnh BC) và cắt các cạnh CA, AB thứ tự ở \(B_1,C_1\). Kẻ GF // BC ( F thuộc BC). CMR: \(\frac{1}{GA_1}+\frac{1}{GB_1}=\frac{1}{GC_1}\)

Những câu hỏi liên quan
Bài 6: Cho hình thang ABCD có hai đáy là AB và CD. Một đường thẳng song song với AB cắt các cạnh bên AD, BC theo thứ tự ở E và F. a) Chứng minh ED/AD + BF/BC 1b) Các đường chéo của hình thang cắt nhau tại O. Chứng minh OA.OD OB.OC.Bài 7: Cho tam giác ABC nhọn, M là trung điểm của BC, E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với AC cắt AB ở D, cắt AM ở K. Qua E kẻ đường thẳng song song với AB cắt AC ở F.a) Chứng minh CF DKb) Gọi H là trực tâm của tam giác ABC. Đường thẳng qua H vu...
Đọc tiếp
Bài 6: Cho hình thang ABCD có hai đáy là AB và CD. Một đường thẳng song song với AB cắt các cạnh bên AD, BC theo thứ tự ở E và F.
a) Chứng minh ED/AD + BF/BC = 1
b) Các đường chéo của hình thang cắt nhau tại O. Chứng minh OA.OD = OB.OC.
Bài 7: Cho tam giác ABC nhọn, M là trung điểm của BC, E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với AC cắt AB ở D, cắt AM ở K. Qua E kẻ đường thẳng song song với AB cắt AC ở F.
a) Chứng minh CF = DK
b) Gọi H là trực tâm của tam giác ABC. Đường thẳng qua H vuông góc với MH cắt AB và AC theo thứ tự ở I và K’. Qua C kẻ đường thẳng song song với IK’, cắt AH và AB theo thứ tự ở N và P. Chứng minh NC = NP và HI = HK’.
Bài 8: Cho tam giác ABC, điểm M bất kì trên cạnh AB. Qua M kẻ đường thẳng song song với BC cắt AC ở N biết AM = 11 cm, MB = 8 cm, AC = 38 cm. Tính độ dài các đoạn thẳng AN, NC.
Bài 9: Cho góc xAy, trên tia Ax lấy hai điểm D và E, trên tia Ay lấy hai điểm F và G sao cho FD song song với EG. Đường thẳng qua G song song với FE cắt tia Ax tại H. Chứng minh AE 2 = AD.AH.
Bài 10: Cho hình bình hành ABCD. Gọi E là một điểm bất kì trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC ở F và kẻ đường thẳng song song với BD cắt AD ở H. Đường thẳng kẻ quá F song song với BD cắt CD ở G. Chứng minh AH.CD = AD.CG.
Bài 6 :
Tự vẽ hình nhá :)
a) Gọi O là giao điểm của AC và EF
Xét tam giác ADC có :
EO // DC => AE/AD = AO/AC (1)
Xét tam giác ABC có :
OF // DC
=> CF/CB = CO/CA (2)
Từ (1) và (2) => AE/AD + CF/CB = AO/AC + CO/CA = AO + CO/AC = AC/AC = 1 => đpcm
Bài 7 :
a) Do EF // AB => CF / CA = EF / AB => CF / EF = AC / AB (1)
Dựng MG // AC và M là trung điểm của cạnh BC => GM là đường trung bình của tam giác ABC => G là trung điểm của cạnh AB =>AG = BG
Do DK // GM => AD / AG = DK / GM => AD / BG = DK / GM
=> DK / AD = GM / BG = \(\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB} \left(2\right)\)
Từ (1) và (2) => CF / EF = DK / AD
Mà tứ giác ADEF là hình bình hành ( vì EF // AD và DE // AF ) nên AD = È
=> CF = DK ( đpcm )
Bài 8 :
Ta có : AB = AM + MB = 11 + 8 = 19 ( cm )
Áp dụng hệ quả định lí Ta-lét vào tam giác ABC, ta có :
AM / AB = AN / AC => AM + AB / AB = AN + AC / AC => 19 + 11 / 19 = AN + 38 / 38 => 30/19 = 38 + AN / 38
=> 1140 = 19.AN + 722
=> AN = ( 1140 - 722 ) / 19 = 22 ( cm )
=> NC = 38 - 12 = 26 ( cm )
chắc sang năm mới làm xong mất
sang năm mk giúp bn na
Xem thêm câu trả lời
Bài 1 : Cho tam giác đều ABC . Lấy các điểm D,E,F theo thứ tự thuộc các cạnh AB,BC,CA sao cho AD=BE=CF . CMR tam giác DEF là tam giác đều
Bài 2 Cho tam giác ABC . Các tia p/g của các góc B,C cắt nhau ở I . Qua I kẻ đường thẳng //BC . Gọi giao điểm của đường thẳng này với AB , AC theo thứ tự là D, E . CMR DE=BD+CE
CÁC BÀI GIÚP MK VỚI BÀI NÀO CŨNG ĐƯỢC MK ĐG CẦN GẤP
Cho tam giác abc có trung tuyến AD trọng tâm G và AB bằng 18 cm BC = 16 cm
a> một đường thẳng d1 đi qua G và song song vs cạnh BC cắt AB tại M .Tính độ dài đoạn thẳng BM
b>Kẻ đường thẳng d2 đi qua G và song song vs cạnh DM cắt cạnh BC tại N . Tính độ dài đoạn BN
Đề năm 2008-2009 ai thần đồng giúp
1.Hinh thang ABCD đáy lớn ;CD. Qua A vẽ đường thẳng AK // BC cắt BD tại E. Qua B vẽ đường thẳng BI // AD cắt AC tại F ( K; I thuộc CD). CMR
a, EF//AB
b, _{AB^2}CD.EF
2. Cho 1 điểm M nằm tring tam giác ABC. Đương thẳng qua M và trọng yaam G của tam giác cắt BC , CA và AB theo thứ tự D,E,F. CMR frac{MD}{GD}+frac{ME}{GE}+frac{MF}{GF}3
3.Cho tam giác ABC cân tại A. Hai điểm D và E theo thứ tự thay đổi trên AB và BC. Kẻ DF vuông góc BC. CMR: nếu EFfrac{BC}{2}thì đường thẳng qua E và vuông góc...
Đọc tiếp
1.Hinh thang ABCD đáy lớn ;CD. Qua A vẽ đường thẳng AK // BC cắt BD tại E. Qua B vẽ đường thẳng BI // AD cắt AC tại F ( K; I thuộc CD). CMR
a, EF//AB
b, \(_{AB^2}\)=CD.EF
2. Cho 1 điểm M nằm tring tam giác ABC. Đương thẳng qua M và trọng yaam G của tam giác cắt BC , CA và AB theo thứ tự D,E,F. CMR \(\frac{MD}{GD}+\frac{ME}{GE}+\frac{MF}{GF}=3\)
3.Cho tam giác ABC cân tại A. Hai điểm D và E theo thứ tự thay đổi trên AB và BC. Kẻ DF vuông góc BC. CMR: nếu EF=\(\frac{BC}{2}\)thì đường thẳng qua E và vuông góc với DE luôn đi qua I diểm cố định.
4. Cho tam giác ABC trọng tâm G , đường thẳng d qua G cắt các cạnh AB và AC tại M<N. CMR:AM.AN=AM.NC+AN.MB
5. Cho tam giác Abc vuông tại A. Giả sử đường cao AH , trung tuyến BM, và phân giác trong CN đồng quy. CMR BH=AC
6. CHo tâm giác ABC. AM, AN và CP cắt nhau tại I. TÌm I để\(\frac{AI}{IM}+\frac{BI}{IN}+\frac{CI}{IP}\) nhỏ nhất
7. Cho tứ giác ABCD. Đường thẳng A// BC tại P và đường thẳng qua B// AD cắt AC ở Q.CMr PQ//CD
1. Cho tam giác ABC, điểm D thuộc cạnh BC. Qua D kẻ các đường thẳng song song AB và AC chúng cắt AB,AC theo thứ tự ở E và F. Chứng minh hệ thức: AE/AB+AF/AC12. Cho tam giác ABC, 1 đường thẳng song song với BC cắt các cạnh AB, AC theo thứ tự ở D và E. Qua C kẻ đường thẳng song song với EB cắt AB ở F. Chứng minh hệ thức AB2AD*AF3.Cho tam giác ABC( ABAC) đường phân giác AD. Qua trung điểm M của BC kẻ đường thẳng song song với AD cắt AC và AB theo thứ tự ở E và K. Chứng minh rằng:a. AEAKb. DKCE
Đọc tiếp
1. Cho tam giác ABC, điểm D thuộc cạnh BC. Qua D kẻ các đường thẳng song song AB và AC chúng cắt AB,AC theo thứ tự ở E và F. Chứng minh hệ thức: AE/AB+AF/AC=1
2. Cho tam giác ABC, 1 đường thẳng song song với BC cắt các cạnh AB, AC theo thứ tự ở D và E. Qua C kẻ đường thẳng song song với EB cắt AB ở F. Chứng minh hệ thức AB2=AD*AF
3.Cho tam giác ABC( AB<AC) đường phân giác AD. Qua trung điểm M của BC kẻ đường thẳng song song với AD cắt AC và AB theo thứ tự ở E và K. Chứng minh rằng:
a. AE=AK
b. DK=CE
(Bài này làm như nào vậy mn?)Cho tứ diện với 4 đỉnh là A, B, C, D. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, CD, AC, BD, AD, BC; A_1,B_1,C_1,D_1 lần lượt là trọng tâm các mặt BCD, ACD, ABD, ABC và G là trọng tâm tứ diện. Chọn ngẫu nhiên 5 điểm trong số 15 điểm trên. Khi đó, xác suất để 5 điểm được chọn cùng nằm trên một mặt phẳng bằng bao nhiêu?A. 71/1001B. 75/1001C. 74/1001D.10/143
Đọc tiếp
(Bài này làm như nào vậy mn?)
Cho tứ diện với 4 đỉnh là A, B, C, D. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, CD, AC, BD, AD, BC; \(A_1,B_1,C_1,D_1\) lần lượt là trọng tâm các mặt BCD, ACD, ABD, ABC và G là trọng tâm tứ diện. Chọn ngẫu nhiên 5 điểm trong số 15 điểm trên. Khi đó, xác suất để 5 điểm được chọn cùng nằm trên một mặt phẳng bằng bao nhiêu?
A. 71/1001
B. 75/1001
C. 74/1001
D.10/143
(Bài này làm như nào vậy mn?)Cho tứ diện với 4 đỉnh là A, B, C, D. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, CD, AC, BD, AD, BC; A_1,B_1,C_1,D_1 lần lượt là trọng tâm các mặt BCD, ACD, ABD, ABC và G là trọng tâm tứ diện. Chọn ngẫu nhiên 5 điểm trong số 15 điểm trên. Khi đó, xác suất để 5 điểm được chọn cùng nằm trên một mặt phẳng bằng bao nhiêu?A. 71/1001B. 75/1001C. 74/1001D.10/143
Đọc tiếp
(Bài này làm như nào vậy mn?)
Cho tứ diện với 4 đỉnh là A, B, C, D. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, CD, AC, BD, AD, BC; \(A_1,B_1,C_1,D_1\) lần lượt là trọng tâm các mặt BCD, ACD, ABD, ABC và G là trọng tâm tứ diện. Chọn ngẫu nhiên 5 điểm trong số 15 điểm trên. Khi đó, xác suất để 5 điểm được chọn cùng nằm trên một mặt phẳng bằng bao nhiêu?
A. 71/1001
B. 75/1001
C. 74/1001
D.10/143
Cho tam giác ABC, điểm I nằm trong tam giác, các tia AI, BI, CI cắt các cạnh BC, AC, AB theo thứ tự ở D, E, F. Qua A kẻ đường thẳng song song với BC cắt tia CI tại H và cắt tia BI tại K. Chứng minh:a)
A
K
B
D
H
A
D
C
;
b)
A
F...
Đọc tiếp
Cho tam giác ABC, điểm I nằm trong tam giác, các tia AI, BI, CI cắt các cạnh BC, AC, AB theo thứ tự ở D, E, F. Qua A kẻ đường thẳng song song với BC cắt tia CI tại H và cắt tia BI tại K. Chứng minh:
a) A K B D = H A D C ;
b) A F B F + A E C E = A I I D .
Cho tam giác ABC có G là trọng tâm. Một đường thẳng đi qua G cắt các cạnh AB, AC theo thứ tự ở C', B' và cắt tia đối của tia CB ở A'. Cmr:
1/GA' +1/GB'=1/GC'