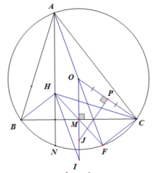
cho tam giác ABC nội tiếp (O), \(\widehat{BOC}=120\)độ, H là trực tâm của tam giác. Gọi M là 1 điểm trên cung BC không chứa điểm A, N là điểm đối xứng của M qua AB, P là điểm đối xứng của M qua AC. Tính Min của \(\frac{1}{MB}+\frac{1}{MC}\)

Những câu hỏi liên quan
cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm O. H là trực tâm của tam giác. Gọi M là một điểm trên cung BC không chứa điểm A( M không trùng với B và C). Gọi N và P lần lượt là điểm đối xứng của M qua các đường thẳng AB và AC. câu a: chúng minh N, H, P thẳng hàng. câu b: Khi góc BOC = 120 độ, xác định vị trí của điểm M sao cho 1/MB + 1/ MC đạt giá trị nhỏ nhất
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). H là trực tâm của tam giác ABC. Lấy 1 điểm M bất kì trên cung BC không chứa điểm A (M không trùng với B,C). Lấy điểm P đối xứng với điểm M qua cạnh AC. Chứng minh rằng AHCP nội tiếp đường tròn
Chú ý góc APC = góc AMC ( t/c đối xứng)
Mà góc AMC = Góc ABC
Chú ý : CH vuông góc AB
Từ đây có ngay kết quả nhe
Đúng 0
Bình luận (0)
cho tam giác abc nhọn .vẽ các đường cao bd ce gọi h là trực tâm của tam giác abc .a)chưng minh tứ giác bedc nội tiếp. b) gọi m là điểm đối xứng h qua bc chứng minh tứ giác abmc nội tiếp. c) gọi n là điểm đối xứng của h qua trung điểm I của bc chứng minh abnc nội tiếp
a: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
b: góc HBC+góc HCB=90 độ-góc ABC+90 độ-góc ACB
=góc BAC
=>góc BHC=180 độ-góc BAC
=>góc BHC+góc BAC=180 độ
H đối xứng M qua BC
=>BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM
HC=MC
BC chung
=>ΔBHC=ΔBMC
=>góc BMC=góc BHC
=>góc BMC+góc BAC=180 độ
=>ABMC nội tiếp
c: Xét tứ giác BHCN có
BC cắt HN tại trung điểm của mỗi đường
=>BHCN là hìnhbình hành
=>góc BHC=góc BNC
=>góc BNC+góc bAC=180 độ
=>ABNC nội tiếp
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O), trực tâm H. Giả sử M là một điểm trên cung BC không chứa A. Gọi N, P lần lượt là điểm đối xứng của M qua AB, AC
a. cmr tứ giác AHCP nội tiếp
b. chứng minh ba điểm N, H, P thẳng hàng
Giúp mình với nha. cảm ơn nhiều!
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O) với trực tâm là H. Giả sử M là một điểm trên cung BC không chứa A (M khác B, M khác C). Gọi N, P theo thứ tự là điểm đối xứng của M qua các đường thẳng AB, AC.
a) Chứng minh tứ giác AHCP nội tiếp.
b) Chứng minh ba điểm N, H, P thẳng hàng.
c) Tìm vị trí của M để độ dài NP lớn nhất.
1. Gọi giao điểm của CH với AB là I, AH với BC là K,Ta có tứ giác BIHK nội tiếp mà (1) Ta lại có (hai góc nội tiếp cùng chắn một cung)
(t/c đối xứng) (2)Từ (1) và (2) Suy ra tứ giác AHCP nội tiếp.2. Tứ giác AHCP nội tiếp Ta lại có mà
(3)Chứng minh tương tự câu 1) ta có tứ giác AHBN nội tiếp
(4)
Từ (3) và (4) N, H, P thẳng hàng
3.
=> (<180độ) không đổi
Có AN = AM = AP, cần chứng minh NP = 2.AP.sinBAC
=> NP lớn nhất <=> AP lớn nhất mà AP = AM
AM lớn nhất <=> AM là đường kính của đường tròn (O)
Vậy NP lớn nhất <=> AM là đường kính của đường tròn.
a)gọi I là giao điểm của CH và AB
K là giao điểm AH và BC
ta có :góc IBK+ AHC=180 độ
mà góc IBK= APC
=> tứ giác AHCP nội tiếp
b)Ta có Góc AHP= ACP cùng chắn cung AP (
mà góc ACP=ACM (1)
=> góc ACP= AHP
cmtt
gócAHN=ABN cùng chắn cung AP
mà ABN=ABM => AHN=ABM(2)
Xét tứ giác ABMC nội tiếp
gócACM+ABM=180 độ (3)
từ (1)(2)(3) =>
góc AHP+AHN=180 độ
=> N,H,P thẳng hàng
ta có góc MAN=2BAM,
góc MAP=2MAC
=> NAP=2(BAM+MAC)
=2 x góc BAC (ko đổi )
ta có AM=AN=AP
NP=2AP.sin BAC=2AM.sinBAC
=> NP lớn nhất <=> AM Max
Xem thêm câu trả lời
Cho tam giác ABC nhọn (AB AC) nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. Gọi M là trung điểm của BCc) Gọi N là giao điểm của AH với đường tròn (O) (N khác A). Gọi D là điểm bất kì trên cung nhỏ NC của đường tròn tâm (O) (D khác N và C). Gọi E là điểm đối xứng với D qua AC, K là giao điểm của AC và HE. Chứng minh rằng ACH ADK.
Đọc tiếp
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. Gọi M là trung điểm của BC
c) Gọi N là giao điểm của AH với đường tròn (O) (N khác A). Gọi D là điểm bất kì trên cung nhỏ NC của đường tròn tâm (O) (D khác N và C). Gọi E là điểm đối xứng với D qua AC, K là giao điểm của AC và HE. Chứng minh rằng ACH = ADK.
Ta có NHC = ABC (cùng phụ với HCB) (1)
Vì ABDC là tứ giác nội tiếp nên ABC = ADC (2)
Vì D và E đối xứng nhau qua AC nên AC là trung trực DE suy ra
∆ADC = ∆AEC (c.c.c) => ADC = AEC (3)
Tương tự ta có AEK = ADK
Từ (1), (2), (3) suy ra NHC = AEC => AEC + AHC = NHC + AHC = 180o
Suy ra AHCE là tứ giác nội tiếp => ACH = AEK = ADK (đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp (O). Gọi H là trực tâm của tam giác ABC, E là điểm đối xứng của H qua BC; F là điểm đối xứng của H qua trung điểm I của BC.
giúp mình với:
cho đường tròn (O) ngoại tiếp tam giác ABC với trực tâm H, M là một điểm bất kì trên cung BC không chứa A.
a) Xác định vị trí M để tứ giác BHCM là hình bình hành.
b) gọi các điểm đối xứng của M qua AB, AC lần lượt là N, E. chứng minh tứ giác AHBN, AHCE nội tiếp được.
c) chứng minh ba điểm N, H, E thẳng hàng.
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (o) có trực tâm là H. Gọi M là diểm trên cung BC không chứa diểm A ( M khác B,C). Gọi N, P theo thứ tự là điểm đối xứng của M qua các đường thẳng AB AC
Chứng minh tứ giác AHCP là tứ giác nội tiếp
N, H, P thẳng hàng
Tìm vị trí của M dể ộ dài doạn NP lớn nhất


















