câu1:cho phương trình bậc hai:X2+4X-m+3=0(1). Tìm m để
1)Pt(1) có hai nghiệm trái dấu
2) Pt (1) có hai nghiệm x1,x2, thoả mãn X21+X22=16
Những câu hỏi liên quan
Cho phương trình bậc hai x 2 + 4x + m = 0 (1)
c) Xác định m để phương trình (1) có hai nghiệm x 1 và x 2 thỏa mãn x 1 2 + x 2 2 = 10.
c) Để phương trình (1) có hai nghiệm x1 và x2 ⇔ Δ' ≥ 0 ⇔ 4 - m ≥ 0 ⇔ m ≤ 4
Theo Vi-et ta có: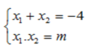 
Ta có: x 1 2 + x 2 2 = 10 ⇔ x 1 + x 2 2 - 2x1x2 = 10
⇔ - 4 2 - 2m = 10 ⇔ 16 - 2m = 10 ⇔ m = 3 (TM)
Vậy với m = 3 thì phương trình (1) có hai nghiệm thõa mãn: x 1 2 + x 2 2 = 10
Đúng 0
Bình luận (0)
Cho pt xã -4x4 m=0 (*). Tìm m để phương trình (*) có 2 nghiệm x1, x2 thỏa mãn hệ thức 2x1 + x2 = 1 Cho pt: 2x2 3x-2m +3 = 0 ("). Tìm m để phương trình (") có 2 nghiệm phân biệt x1, x2 thỏa mãn hệ thức x1/x2 + xz/x1 =3 Cho pt xã 4x - m + 3 = 0 (*). Tìm m để phương trình (*) có 2 nghiệm x1, x2 thỏa mãn hệ thức x1-x2=7 Giải gấp chi tiết giúp e vs ạ
cho phương trình x2-2x+3m-2=0 (1).
Tìm m để pt có hai nghiệm x1,x2 TM:x12+x22=20
Để PT có hai nghiệm x1,x2 thì:
Δ' = (-1)2 - 1.(3m-2) > 0
<=> m <1
Áp dụng Viet, ta có :
x1 + x2 = -2
x1.x2 = 3m-2
Ta có :
x12 + x22 = (x1 + x2)2 - 2x1.x2 = (-2)2 - 2(3m-2) = 20
<=> 4 -6m + 4 = 20
<=> m = -2 (thỏa mãn)
Vậy m = -2
Đúng 2
Bình luận (0)
Cho phương trình bậc hai, ẩn số là x : x2 – 3x + k – 1 = 0.
Tìm giá trị của k sao cho phương trình đã cho có hai nghiệm x1, x2 thoả mãn điều kiện
x12 – x22 = 15.
\(\Delta=9-4\left(k-1\right)=13-4k\ge0\Rightarrow k\le\dfrac{13}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=k-1\end{matrix}\right.\)
\(\left(x_1-x_2\right)\left(x_1+x_2\right)=15\Leftrightarrow x_1-x_2=5\)
Kết hợp hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1-x_2=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=4\\x_2=-1\end{matrix}\right.\)
\(x_1x_2=k-1\Rightarrow k-1=-4\Rightarrow k=-3\)
Đúng 1
Bình luận (2)
Cho phương trình: x2+mx+1=0 (1), m là tham số
a)Giải phương trình (1) khi m=4.
b)Tìm giá trị m để pt (1) có 2 nghiệm x1,x2 thõa mãn: x12/x22 + x22/x12 >7
Xem chi tiết
Cho phương trình (m-1)x2 + (m+1)x+2=0 với m \(\ne\) 0.
Tìm giá trị của m để hai nghiệm x1, x2 của phương trình thoả mãn | x12- x22 | = 3.
Bổ sung thêm điều kiện đề với \(m\ne1\) nữa nhé: )
Nhẩm nghiệm: \(a-b+c=0\) \(\left(m-1-m-1+2=0\right)\)
\(\Rightarrow\) PT có 2 nghiệm \(x_1=-1;x_2=\dfrac{2}{m-1}\)
Nếu \(x_1^2-x_2^2=3\):
\(\left(-1\right)^2-\left(\dfrac{2}{m-1}\right)^2=3\)
=> Không có giá trị m thỏa mãn.
Nếu \(x_1^2-x_2^2=-3\):
\(\left(-1\right)^2-\left(\dfrac{2}{m-1}\right)^2=-3\\ \Rightarrow m=2\left(TM\right)\)
Đúng 3
Bình luận (0)
Cho pt: x2 - (m + 2) + 7m - 2m2 - 3 = 0 (với x là ẩn số) (1)
a) Chứng tỏ phương trình (1) luôn có 2 nghiệm phân biệt.
b) Tìm m để phương trình (1) có hai nghiệm x1 , x2 thỏa hệ thức:
2(x12 - x22) - 5x1x2 = 2
phương trình bạn copy thiếu ak bạn ơi?
Đúng 0
Bình luận (3)
Cho pt: x^2+4x-m^2-1=0 Tìm m để pt có nghiệm x1,x2 thoả mãn x1/x2+x2/x1= -5/2
Lời giải:
$\Delta'=4+m^2+1=5+m^2>0$ với mọi $m\in\mathbb{R}$ nên pt luôn có 2 nghiệm phân biệt với mọi $m\in\mathbb{R}$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=-4\\ x_1x_2=-(m^2+1)\end{matrix}\right.\)
Khi đó:
\(\frac{x_1}{x_2}+\frac{x_2}{x_1}=\frac{-5}{2}\Leftrightarrow \frac{x_1^2+x_2^2}{x_1x_2}=-\frac{5}{2}\)
\(\Leftrightarrow \frac{(x_1+x_2)^2-2x_1x_2}{x_1x_2}=\frac{-5}{2}\Leftrightarrow \frac{(x_1+x_2)^2}{x_1x_2}=-\frac{1}{2}\)
\(\Leftrightarrow \frac{16}{-(m^2+1)}=\frac{-1}{2}\Leftrightarrow m^2+1=32\)
\(\Rightarrow m=\pm \sqrt{31}\)
Đúng 1
Bình luận (1)
Cho phương trình: x^2 + 4x + m + 1 = 0. Tìm m để pt có 2 nghiệm x1, x2 thỏa mãn pt \(\dfrac{x1}{x2}+\dfrac{x2}{x1}=\dfrac{10}{3}\)
PT có 2 nghiệm `<=> \Delta' >0 <=> 2^2-1.(m+1)>0<=> m<3`
Viet: `x_1+x_2=-4`
`x_1 x_2=m+1`
`(x_1)/(x_2)+(x_2)/(x_1)=10/3`
`<=> (x_1^2+x_2^2)/(x_1x_2)=10/3`
`<=> ((x_1+x_2)^2-2x_1x_2)/(x_1x_2)=10/3`
`<=> (4^2-2(m+1))/(m+1)=10/3`
`<=> m=2` (TM)
Vậy `m=2`.
Đúng 1
Bình luận (0)