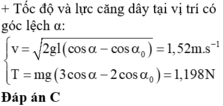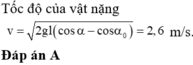Một con lắc đơn gồm hòn bi nặng 100g và sợi dây dài 1 m. Kéo cho dây làm với đường thẳng đứng 600 rồi thả nhẹ. Tính vận tốc của con lắc và lực căng của dây treo khi nó đi qua vị trí mà dây hợp với phương thẳng đứng 1 góc 0,30,45 .

Những câu hỏi liên quan
Một con lắc đơn gồm vật nặng khối lượng m 1 kg treo vào sợi dây có chiều dài l 40 cm. Kéo vật đến vị trí dây làm với đường thẳng đứng một góc
α
0
60
0
rồi thả nhẹ. Bỏ qua sức cản không khí. Lấy g 10
m
/
s
2
. Tìm vận tốc của con lắc và lực căng của sợi dây khi nó đi qua: a) Vị trí ứng với góc
α
30
0...
Đọc tiếp
Một con lắc đơn gồm vật nặng khối lượng m = 1 kg treo vào sợi dây có chiều dài l = 40 cm. Kéo vật đến vị trí dây làm với đường thẳng đứng một góc α 0 = 60 0 rồi thả nhẹ. Bỏ qua sức cản không khí. Lấy g = 10 m / s 2 . Tìm vận tốc của con lắc và lực căng của sợi dây khi nó đi qua:
a) Vị trí ứng với góc α = 30 0 .
b) Vị trí cân bằng.
Một CLĐ dây treo dài 90 cm, vật nặng 400 gam. Kéo vật sao cho dây treo hợp với phương thẳng đứng góc 30o rồi thả nhẹ. Lấy g = 10 m/s2
a. Tính vận tốc vật nặng khi nó qua vị trí cân bằng
b. Tính vận tốc vật và lực căng dây khi con lắc có li độ góc là 12o
c. Tính lực căng dây khi con lắc ở vị trí cao nhất trong quá trình dao động
Một con lắc đơn có sợi dây dài 1m và vật nặng có khối lượng 500g. Kéo vật lệch khỏi vị trí cân bằng sao cho cho dây làm với đường thẳng đứng một góc 60o rồi thả nhẹ. Lấy
g
10
(
m
/
s
2
)
a. Xác định cơ năng của con lắc đơn trong quá trình chuyển độngb. Tính vận tốc của con lắc khi nó đi qua vị trí mà dây làm với đường thẳng đứng góc
3...
Đọc tiếp
Một con lắc đơn có sợi dây dài 1m và vật nặng có khối lượng 500g. Kéo vật lệch khỏi vị trí cân bằng sao cho cho dây làm với đường thẳng đứng một góc 60o rồi thả nhẹ. Lấy g = 10 ( m / s 2 )
a. Xác định cơ năng của con lắc đơn trong quá trình chuyển động
b. Tính vận tốc của con lắc khi nó đi qua vị trí mà dây làm với đường thẳng đứng góc 30 0 ; 45 0 và xác định lực căng của dây ở hai vị trí đó. Lấy g=10m/s2
c. Xác định vị trí để vật có v= 1,8 m/s
d. Ở vị trí vật có độ cao 0,18m vật có vận tốc bao nhieu
e. Xác định vận tốc tại vị trí 2 w t = w đ
f. Xác định vị trí để 2 w t = 3 w đ , tính vận tốc và lực căng khi đó
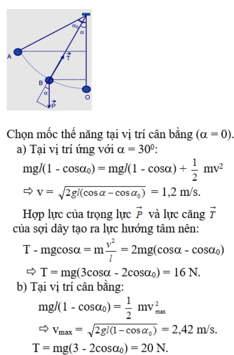
Chọn mốc thế năng ở vị trí cân bằng
a. Ta có cơ năng
W = m g z = m g l ( 1 − cos 60 0 ) = 0 , 5.10.1 ( 1 − 0 , 5 ) = 2 , 5 ( J )
b. Theo định luật bảo toàn cơ năng
W A = W B ⇒ m g z A = 1 2 m v B 2 + m g z B ⇒ v B = 2 g ( z A − z B ) ( 1 ) M à z A = H M = l − O M = l − l cos α 0 z B = l − l cos α
Thay vào ( 1 ) ta có
v B = 2 g l ( cos α − cos α 0 ) + K h i α = 30 0 ⇒ v B = 2 g l ( cos 30 0 − cos 60 0 ) ⇒ v B = 2.10.1 ( 3 2 − 1 2 ) ≈ 2 , 71 ( m / s )
+ K h i α = 45 0 ⇒ v B = 2 g l ( cos 45 0 − cos 60 0 ) ⇒ v B = 2.10.1 ( 2 2 − 1 2 ) ≈ 2 , 035 ( m / s )
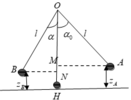
Xét tai B theo định luật II Newton ta có: P → + T → = m a →
Chiếu theo phương của dây
T − P y = m a h t ⇒ T − P cos α = m v 2 l ⇒ T − m g cos α = 2 m g ( cos α − cos α 0 ) ⇒ T = m g ( 3 cos α − 2 cos α 0 )
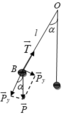
Khi α = 30 0 ⇒ T = m g ( 3 cos 30 0 − 2 cos 60 0 )
⇒ T = 0 , 5.10 ( 3. 3 2 − 2. 1 2 ) = 7 , 99 ( N )
Khi α = 45 0 ⇒ T = m g ( 3 cos 45 0 − 2 cos 60 0 )
⇒ T = 0 , 5.10 ( 3. 2 2 − 2. 1 2 ) = 5 , 61 N
Lưu ý: Khi làm trắc nghiệm thì các em áp dụng luôn hai công thức
+ Vận tốc của vật tại vị trí bất kỳ: v B = 2 g l ( cos α − cos α 0 )
+ Lực căng của sợi dây: T = m g ( 3 cos α − 2 cos α 0 )
c. Gọi C là vị trí để vật có v= 1,8m/s
Áp dụng công thức v C = 2 g l ( cos α − cos α 0 )
1 , 8 = 2.10.1 ( cos α − cos 60 0 ) ⇒ cos α = 0 , 662 ⇒ α = 48 , 55 0
Vật có đọ cao
z C = l − l cos α = 1 − 1.0 , 662 = 0 , 338 ( m )
d. Gọi D là vị trí vật có độ cao 0,18m
Áp dụng công thức
z D = l − l cos α ⇒ 0 , 18 = 1 − 1. cos α ⇒ cos α = 0 , 82
Áp dụng công thức
v D = 2 g l ( cos α − cos α 0 ) = 2.10.1. ( 0 , 82 − 0 , 5 ) = 2 , 53 ( m / s )
e. Gọi E là vị trí mà 2 w t = w đ Theo định luật bảo toàn cơ năng W A = W E
W A = W d E + W t E = 3 2 W d E ⇒ 2 , 5 = 3 2 . 1 2 . m v E 2 ⇒ v E = 2 , 5.4 3. m = 10 3.0 , 5 = 2 , 581 ( m / s )
f. Gọi F là vị trí để 2 w t = 3 w đ
Theo định luật bảo toàn cơ năng W A = W F
W A = W d F + W t F = 5 3 W t F ⇒ 2 , 5 = 5 3 . m g z F ⇒ z F = 2 , 5.3 5. m . g = 0 , 3 ( m ) M à z F = l − l cos α F ⇒ 0 , 3 = 1 − 1. cos α F ⇒ cos α F = 0 , 7 ⇒ α F = 45 , 573 0
Mặt khác v F = 2 g l ( cos α F − cos 60 0 ) = 2.10.1 ( 0 , 7 − 0 , 5 ) = 2 ( m / s )
Xét tại F theo định luật II Newton P → + T → = m a →
Chiếu theo phương của dây
− P cos α F + T F = m v F 2 l ⇒ − 0 , 5.10.0 , 7 + T F = 0 , 5. 2 2 1 ⇒ T = 5 , 5 ( N )
Đúng 0
Bình luận (0)
Một con lắc đơn có chiều dài l=1m. Kéo cho dây treo làm với phương thẳng đứng một góc =45o rồi buông nhẹ. Lấy g=10m/s2 Bỏ qua ma sát. Tính vận tốc của con lắc và lực căng dây khi nó qua vị trí có góc lệch =30o.
vận tốc vật ở góc lệch a: \(v_{\left(\alpha\right)}=\pm\sqrt{2gl\left(\cos\alpha_2-\cos\alpha_1\right)}\) ( thuộc càng tốt )
lực căng dây:\(T_c=mg\left(3\cos\alpha_2-2\cos\alpha_1\right)\)
Bây giờ mình sẽ đi chứng minh 2 công thức trên :D
Chọn mốc tính thế năng tại vị trí thấp nhất của vật
Cơ năng của vật ứng với góc \(\alpha_1=45^0\) là:
\(W_1=W_{đ1}+W_{t1}=\dfrac{1}{2}mv_1^2+mgz_1=0+mgl\left(1-\cos\alpha_1\right)\)
Cơ năng của vật ứng với góc \(\alpha_2=30^0\) là:
\(W_2=W_{đ2}+W_{t2}=\dfrac{1}{2}mv_2^2+mgz_2=\dfrac{1}{2}mv_2^2+mgl\left(1-\cos\alpha_2\right)\)
Bỏ qua ma sát ( sức cản kk ) cơ năng được bảo toàn:
\(W_1=W_2\) \(\Leftrightarrow0+mgl\left(1-\cos\alpha_1\right)=\dfrac{1}{2}mv_2^2+mgl\left(1-\cos\alpha_2\right)\)
\(\Leftrightarrow v_2=\pm\sqrt{2gl\left(\cos\alpha_2-\cos\alpha_1\right)}=\pm1,78\left(m/s\right)\)
Chọn trục tọa độ Oy hướng tâm:
Phương trình định luật II Niu tơn cho vật:
\(a=\dfrac{-P\cos\alpha+T_c}{m}\) trong đó: \(a=a_{ht}=\dfrac{v^2}{R}=\dfrac{v^2}{l}\) và v thì đã được chứng minh ở câu trên
Từ đấy ta có: \(\dfrac{\left(\pm\sqrt{2gl\left(\cos\alpha_2-\cos\alpha_1\right)}\right)^2}{l}=\dfrac{-P\cos\alpha_2+T_c}{m}\)
\(\Rightarrow2mg\left(\cos\alpha_2-\cos\alpha_1\right)=-P\cos\alpha_2+T_c\)
\(\Rightarrow T_c=mg\left(3\cos\alpha_2-2\cos\alpha_1\right)=\) bạn thay số nốt hộ mình là xong :D hơi thấm mệt
Đúng 2
Bình luận (0)
Một con lắc đơn gồm một quả cầu nhỏ, khối lượng 100g treo vào trần nhà bằng một sợi dây dài 1m, ở nới có gia tốc trọng trường g 9,8 m/s2. Bỏ qua mọi ma sát. Kéo vật nặng lệch một góc 300 rồi buông nhẹ. Tốc độ và lực căng dây tại vị trí dây treo hợp với phương thẳng đứng 100 là: A. 1,620 m/s; 0,586 N. B. 1,243 m/s; 1,243 N. C. 1,526 m/s; 1,198 N. D. 1,079 m/s; 0,616 N.
Đọc tiếp
Một con lắc đơn gồm một quả cầu nhỏ, khối lượng 100g treo vào trần nhà bằng một sợi dây dài 1m, ở nới có gia tốc trọng trường g = 9,8 m/s2. Bỏ qua mọi ma sát. Kéo vật nặng lệch một góc 300 rồi buông nhẹ. Tốc độ và lực căng dây tại vị trí dây treo hợp với phương thẳng đứng 100 là:
A. 1,620 m/s; 0,586 N.
B. 1,243 m/s; 1,243 N.
C. 1,526 m/s; 1,198 N.
D. 1,079 m/s; 0,616 N.
Một con lắc đơn có chiều dài 1m.Kéo cho dây làm với đường thẳng đứng góc
45
0
rồi thả nhẹ. Tính vận tốc của con lắc khi nó đi qua vị trí mà dây làm với đường thẳng đứng góc
30
0
.Lấy
g
10
m
/
s
2
Đọc tiếp
Một con lắc đơn có chiều dài 1m.Kéo cho dây làm với đường thẳng đứng góc 45 0 rồi thả nhẹ. Tính vận tốc của con lắc khi nó đi qua vị trí mà dây làm với đường thẳng đứng góc 30 0 .Lấy g = 10 m / s 2
Chọn mặt phẳng ngang qua C làm gốc thế năng (hình 94)
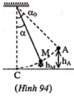
Cơ năng tại A ứng với góc lệch α = 45 0
![]()
Cơ năng tại M ứng với góc lệch α = 30 0
![]()
Định luật bảo toàn cơ năng: W A = W M
![]()
![]()
Đúng 0
Bình luận (0)
Một con lắc đơn gồm vật nặng có khối lượng m gắn với dây treo có chiều dài l. Từ vị trí cân bằng kéo lệch sợi dây sao cho góc lệch của sợi dây với phương thẳng đứng là
α
o
60
o
rồi thả nhẹ. Lấy g 10m/
s
2
. Bỏ qua mọi ma sát. Độ lớn của gia tốc khi lực căng dây có độ lớn bằng trọng lực A.
10
3
m
/...
Đọc tiếp
Một con lắc đơn gồm vật nặng có khối lượng m gắn với dây treo có chiều dài l. Từ vị trí cân bằng kéo lệch sợi dây sao cho góc lệch của sợi dây với phương thẳng đứng là α o = 60 o rồi thả nhẹ. Lấy g = 10m/ s 2 . Bỏ qua mọi ma sát. Độ lớn của gia tốc khi lực căng dây có độ lớn bằng trọng lực
A. 10 3 m / s 2
B. 0 m/ s 2
C. 10 5 3 m / s 2
D. 10 6 3 m / s 2
Một con lắc đơn gồm vật nặng có khối lượng m gắn với dây treo có chiều dài l. Từ vị trí cân bằng kéo lệch sợi dây sao cho góc lệch của sợi dây với phương thẳng đứng là α0 60o rồi thả nhẹ. Lấy g 10m/s2. Bỏ qua mọi ma sát. Độ lớn của gia tốc khi lực căng dây có độ lớn bằng trọng lực
Đọc tiếp
Một con lắc đơn gồm vật nặng có khối lượng m gắn với dây treo có chiều dài l. Từ vị trí cân bằng kéo lệch sợi dây sao cho góc lệch của sợi dây với phương thẳng đứng là α0 = 60o rồi thả nhẹ. Lấy g = 10m/s2. Bỏ qua mọi ma sát. Độ lớn của gia tốc khi lực căng dây có độ lớn bằng trọng lực
![]()
![]()
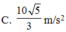
![]()
Chọn D
Biểu thức của lực căng dây: T = mg (3cosα – 2cosαo).
Với T = P = mg => ![]()
+ Gia tốc của vật: ![]()
với an là gia tốc hướng tâm và at là gia tốc tiếp tuyến.
![]()
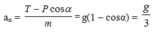
![]()
Đúng 0
Bình luận (0)
Một vật nhỏ được treo vào một sợi dây không giãn, không khối lượng để tạo thành một con lắc đơn có chiều dài 1 m. Vật nặng đang ở vị trí cân bằng thì được kéo đến vị trí mà dây treo làm với phương thẳng đứng một góc 600 rồi thả nhẹ. Bỏ qua mọi lực cản, lấy g 10 m/s2. Trong quá trình chuyển động, tại vị trí mà dây treo hợp với phương thẳng đứng một góc α với cos
α
5
6
thì tốc độ của vật nặng gần bằng: A. 2,6 m/s. B. 6,7 m/s. C. 1,8...
Đọc tiếp
Một vật nhỏ được treo vào một sợi dây không giãn, không khối lượng để tạo thành một con lắc đơn có chiều dài 1 m. Vật nặng đang ở vị trí cân bằng thì được kéo đến vị trí mà dây treo làm với phương thẳng đứng một góc 600 rồi thả nhẹ. Bỏ qua mọi lực cản, lấy g = 10 m/s2. Trong quá trình chuyển động, tại vị trí mà dây treo hợp với phương thẳng đứng một góc α với cos α = 5 6 thì tốc độ của vật nặng gần bằng:
A. 2,6 m/s.
B. 6,7 m/s.
C. 1,8 m/s.
D. 2,9 m/s.
Một con lắc đơn có chiều dài l = 90 cm, khối lượng m = 100g, treo tại O. Kéo con lắc lệch đến vị trí A sao cho dây OA lệch so với đường thẳng đứng một góc 30 độ rồi thả tự do.
a) Tính vận tốc của vật ở vị trí thấp nhất và sức căng của sợi dây tại đó
b) Sau đó dây vướng đinh ở điểm B với OB = 30 cm. Tính góc β khi vật lên cao nhất A