Rút gọn các phân thức sau
a) x3 - 5x2 + 6x/-4x2 + 10x - 4
b) x2 - 3xy + 2y2/x3 + 2x2y - xy2 - 2y3
Rút gọn phân thức sau: x 3 - 5 x 2 + 6 x - 4 x 2 + 10 x - 4
Rút gọn phân thức sau: x 3 - 5 x 2 + 6 x - 4 x 2 + 10 x - 4
Rút gọn phân thức sau: x 2 - 3 x y + 2 y 2 x 3 + 2 x 2 y - x y 2 - 2 y 3
Rút gọn phân thức sau: x 2 - 3 x y + 2 y 2 x 3 + 2 x 2 y - x y 2 - 2 y 3
Phân tích các đa thức sau thành nhân tử:
a/ 2x3 + 3x2 + 2x +3 b/ x2 – x – 12 c/ 4x2 –( x2 + 1)2
d/ 4xy2 – 12x2y + 8xy e/ x2 + x – 6 f/ x3 + 2x2y + xy2 – 4xz2
g/ x3 – 2x2y + xy2 – 25x h/ x2 – 2x – 3 i/ x3 – 3x2 – 9x + 27
a: \(=x^2\left(2x+3\right)+\left(2x+3\right)\)
\(=\left(2x+3\right)\left(x^2+1\right)\)
b: \(=\left(x-4\right)\left(x+3\right)\)
e: =(x+3)(x-2)
a) \(=x^2\left(2x+3\right)+\left(2x+3\right)=\left(2x+3\right)\left(x^2+1\right)\)
b) \(=x\left(x-4\right)+3\left(x-4\right)=\left(x-4\right)\left(x+3\right)\)
c) \(=\left(2x\right)^2-\left(x^2+1\right)^2=\left(x^2-2x+1\right)\left(x^2+2x+1\right)=\left(x-1\right)^2\left(x+1\right)^2\)
d) \(=4xy\left(y-3x+2\right)\)
e) \(=x\left(x-2\right)+3\left(x-2\right)=\left(x-2\right)\left(x+3\right)\)
f) \(=x\left(x^2+2xy+y^2-4z^2\right)=x\left[\left(x+y\right)^2-4z^2\right]=x\left(x+y-2z\right)\left(x+y+2z\right)\)
g) \(=x\left(x^2-2xy+y^2-25\right)=x\left[\left(x-y\right)^2-25\right]=x\left(x-y-5\right)\left(x-y+5\right)\)
h) \(=x\left(x+1\right)-3\left(x+1\right)=\left(x+1\right)\left(x-3\right)\)
i) \(=x^2\left(x-3\right)-9\left(x-3\right)=\left(x-3\right)\left(x^2-9\right)=\left(x-3\right)^2\left(x+3\right)\)
10) x(x-y)+x2-y2
11) x2 -y2 +10x-10y
12) x2-y2 +20x+20y
13) 4x2 -9y2-4x-6y
14) x3-y3+7x2-7y2
15) x3+4x-(y3+4y)
16) x3+y3+2x+2y
17) x3-y3-2x2y+2xy2
18) x3-4x2+4x-xy2
10: \(x\left(x-y\right)+x^2-y^2\)
\(=x\left(x-y\right)+\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(x+x+y\right)\)
\(=\left(x-y\right)\left(2x+y\right)\)
11: \(x^2-y^2+10x-10y\)
\(=\left(x^2-y^2\right)+\left(10x-10y\right)\)
\(=\left(x-y\right)\left(x+y\right)+10\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y+10\right)\)
12: \(x^2-y^2+20x+20y\)
\(=\left(x^2-y^2\right)+\left(20x+20y\right)\)
\(=\left(x-y\right)\left(x+y\right)+20\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y+20\right)\)
13: \(4x^2-9y^2-4x-6y\)
\(=\left(4x^2-9y^2\right)-\left(4x+6y\right)\)
\(=\left(2x-3y\right)\left(2x+3y\right)-2\left(2x+3y\right)\)
\(=\left(2x+3y\right)\left(2x-3y-2\right)\)
14: \(x^3-y^3+7x^2-7y^2\)
\(=\left(x^3-y^3\right)+\left(7x^2-7y^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+7\cdot\left(x^2-y^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+7\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2+7x+7y\right)\)
15: \(x^3+4x-\left(y^3+4y\right)\)
\(=x^3-y^3+4x-4y\)
\(=\left(x^3-y^3\right)+\left(4x-4y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+4\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2+4\right)\)
16: \(x^3+y^3+2x+2y\)
\(=\left(x^3+y^3\right)+\left(2x+2y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)+2\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2+2\right)\)
17: \(x^3-y^3-2x^2y+2xy^2\)
\(=\left(x^3-y^3\right)-\left(2x^2y-2xy^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-2xy\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2-2xy\right)\)
\(=\left(x-y\right)\left(x^2-xy+y^2\right)\)
18: \(x^3-4x^2+4x-xy^2\)
\(=x\left(x^2-4x+4-y^2\right)\)
\(=x\left[\left(x^2-4x+4\right)-y^2\right]\)
\(=x\left[\left(x-2\right)^2-y^2\right]\)
\(=x\left(x-2-y\right)\left(x-2+y\right)\)
Phân tích đa thức sau thành nhân tử:
a) x3 + 2x2y + xy2 - 9x b) 5x2 - 10xy + 5y2
a) x3 + 2x2y + xy2 - 9x
= x(x2 + 2xy + y2 - 9)
= x(x+y)2 - 9
= x(x + y - 3) ( x + y + 3).
b) 5x2 - 10xy + 5y2
= 5(x2 - 2xy + y2)
= 5(x-y)2
Có sai thì xin lỗi ạ
Chứng minh các đẳng thức sau: x 2 + 3 x y + 2 y 2 x 3 + 2 x 2 y - x y 2 - 2 y 3 = 1 x - y
Ta có
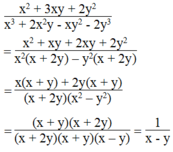
Vế trái bằng vế phải nên đẳng thức được chứng minh.
1. Rút gọn biểu thức:
a. (2x-3)(4x2+6x+9)-2x(4x2-1)
b.(x+y)2+2(x+y)(x-y)+(x-y)2
2.Phân tích đa thức sau thành nhân tử:
a. 2x2y+4xy+2y c. x2-8x+7
b.9x2+6xy-4z2+y2 d. x3+4x2+x-6
1b.=2((x+y)+(x+y)(x-y)+(x-y))=2(x2-y2+x+y+x-y)=2(x2-y2+2x)=2x2-2y2+4x
2a.=4xy+4xy+2y=8xy+2y=2y(4x+1)
b.=(3x)2+2.3x.y+y2-(2z)2=(3x+y)2-(2z)2=(3x+y-2z)(3x+y+2z)
c.=x2-x-7x+7=x(x-1)-7(x-1)=(x-1)(x-7)
\(\left(x+y\right)^2+2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\)
\(=\left(x+y+x-y\right)^2\)
\(=\left(2x\right)^2\)
\(=4x^2\)
hk tốt
^^
Bài 1: Phân tích đa thức thành nhân tử
a) a/ x2 – 2x
b) 2bx – 3ay – 6by + ax
c) x3 +2x2y + xy2 – 4x
d) 4 - x2 – 2xy – y2
đ) 5x2 + 3(x + y)2 – 5y2
e/ 6x2y – 9x
b/ 4x3 – 4x2y + xy2 – 16 x
f) x2 + (2x +y)y – z2
\(a,=x\left(x-2\right)\\ b,=2b\left(x-3y\right)+a\left(x-3y\right)=\left(a+2b\right)\left(x-3y\right)\\ c,=x\left(x^2+2xy+y^2-4\right)=x\left[\left(x+y\right)^2-4\right]=x\left(x+y+2\right)\left(x+y-2\right)\\ d,=4-\left(x+y\right)^2=\left(2-x-y\right)\left(2+x+y\right)\\ đ,=5\left(x-y\right)\left(x+y\right)+3\left(x+y\right)^2=\left(x+y\right)\left(5x-5y+3x+3y\right)\\ =\left(x+y\right)\left(8x-2y\right)=2\left(4x-y\right)\left(x+y\right)\\ e,=3x\left(2xy-3\right)\\ b,=x\left(4x^2-4xy+y^2-4\right)=x\left[\left(2x-y\right)^2-4\right]=x\left(2x-y-2\right)\left(2x-y+2\right)\\ f,=\left(x+y\right)^2-z^2=\left(x+y-z\right)\left(x+y+z\right)\)
a,=x(x−2)b,=2b(x−3y)+a(x−3y)=(a+2b)(x−3y)c,=x(x2+2xy+y2−4)=x[(x+y)2−4]=x(x+y+2)(x+y−2)d,=4−(x+y)2=(2−x−y)(2+x+y)đ,=5(x−y)(x+y)+3(x+y)2=(x+y)(5x−5y+3x+3y)=(x+y)(8x−2y)=2(4x−y)(x+y)e,=3x(2xy−3)b,=x(4x2−4xy+y2−4)=x[(2x−y)2−4]=x(2x−y−2)(2x−y+2)f,=(x+y)2−z2=(x+y−z)(x+y+z)