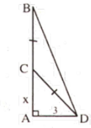
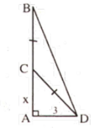
Môt cây bị gãy cách gốc 1,5m, chỗ cây chạm đất cách gốc 2m. Tính chiều cao của cây

Những câu hỏi liên quan
Trong đợt bão, một cây dừa bị gãy ngang thân, ngọn cây chạm đất cách gốc 7m và chiều cao từ gốc cây đến chỗ cây bị gãy 3m
Em hãy tính chiều cao ( từ gốc đến ngọn) của cây dừa đó?
( Kết quả làm tròn đến hàng số thập phân thứ nhất)
Sửa đề: Chiều dài từ gốc cây đến chỗ cây bị gãy là 3m
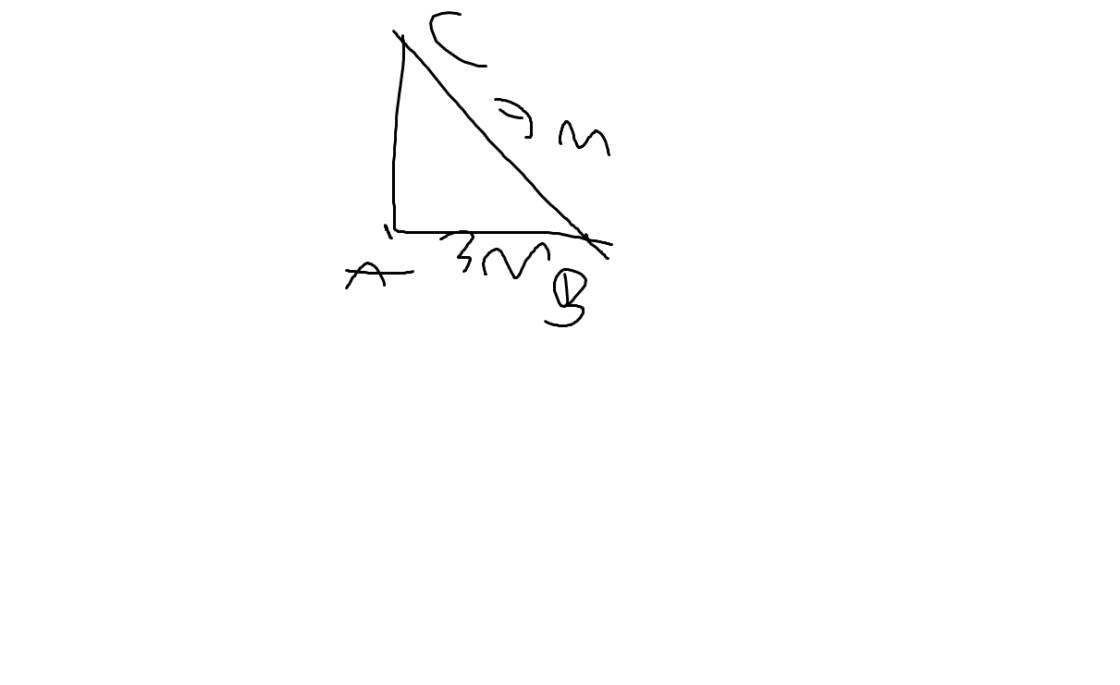
Gọi A là gốc của cái cây
Gọi Clà ngọn của cái cây
Gọi B là chỗ cây bị gãy
Do đó, ta có: \(AB\perp AC\)
Theo đề, ta có: BC=7m; AB=3m
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{7^2-3^2}=2\sqrt{10}\left(m\right)\simeq6,3\left(m\right)\)
Đúng 0
Bình luận (0)
Một cây cau bị gió bão làm gãy ngang thân, ngọn cây cau chạm đất cách gốc 3m, điểm gãy cách gốc 4m. Hỏi chiều cao của cây cau bao nhiêu ?
gọi k/c từ điểm gãy đến ngọn cây là x . Vì cây cau vuông góc với mặt đất nên cây cau gãy tạo với mặt đất hình tam giác vuông =>khoảng cách từ gốc đến điểm gãy và k/c từ ngọn cây đến góc là cạnh góc vuông và x là cạnh huyền Định Lí PTG ta có : 3^2+4^2=x^2 =>x=5 => chiều cao cây = 5+4=9m
Đúng 1
Bình luận (3)
) Do ảnh hưởng của một cơn bão, một cây cột điện có phương thẳng đứng đã bị gió bão làm gãy ngang thân, ngọn cây cột điện chạm đất cách gốc 4m, chiều cao từ gốc cây cột điện đến điểm gãy cao 3m. Em hãy tính chiều cao ban đầu của cây cột điện ?
Phần cây bị gãy tạo với mặt đất và phần còn lại một tam giác vuông.
Gọi gốc cây cột điện là A, điểm bị gãy là B và điểm chạm đất là C, ta có:
Tam giác ABC vuông tại A, AB = 3m; AC = 4m
Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2=3^2+4^2=25\Rightarrow BC=5\left(m\right)\)
Chiều cao cột điện ban đầu là: \(AB+BC=3+5=8\left(m\right)\)
Đúng 4
Bình luận (0)
Một cái cây cao 9m bị gió bão làm gãy ngang thân cây, ngọn cây chạm đất cách gốc 3m. Hỏi điểm gãy cách gốc bao nhiêu?
Giả sử gốc là điểm A, điểm gãy là B và điểm ngọn chạm đất là C, ta có tam giác ABC vuông tại A
Trong đó \(AC=3m\) ; \(AB+BC=9\left(m\right)\)
Áp dụng định lý Pitago:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AB^2+3^2=\left(9-AB\right)^2\)
\(\Leftrightarrow9=81-18AB\)
\(\Rightarrow AB=4\left(m\right)\)
Vậy điểm gãy cách gốc 4m
Đúng 2
Bình luận (0)
Hai cây tre bị gãy cách gốc theo thứ tự 2 thước và 3 thước. Ngọn cây nọ chạm gốc cây kia. Tính từ chỗ thân 2 cây chạm nhau đến mặt đất.
Một cây cao đứng thẳng vuông góc với mặt đất bị gió bão thổi mạnh gãy gặp xuống đón cho bọn cây chạm đất người ta đo được khoảng cách từ ngọn đến gốc cây là 3 m khoảng cách từ khúc Cây bị gãy đến mặt đất là 4 m Hãy tính chiều cao của cây khi chưa bị gãy
Một cây tre cao 8m bị gãy giữa thân, ngọn cây chạm đất cách gốc 4m. Hỏi điểm gãy cách gốc bao nhiêu m?
Điểm gãy cách gốc:
\(\sqrt{8^2-4^2}=4\sqrt{3}\left(m\right)\)
Đúng 1
Bình luận (1)
Tham khảo:
Gọi chiều dài phần còn lại là x (m)
Chiều dài phần gãy là 8−x (m)
Áp dụng định lí Pi-ta-go, ta có:
x2+42=(8−x)2
⇒x2+16=64−16x+x2
⇒x2−x2+16x=64−16
⇒16x=48
⇒x=3
Vậy điểm gãy cách gốc 3m
Đúng 0
Bình luận (1)
Một cây tre cao 8m bị gãy giữa thân, ngọn cây chạm đất cách gốc 4m. Hỏi điểm gãy cách gốc bao nhiêu m?
Gọi khoảng cách từ điểm gãy đến đất là x (m)
Giờ cây tre và mặt đất sẽ tạo thành tam giác vuông có 1 cạnh góc vuông là x (m), cạnh huyền là (8-x) và cạnh góc vuông còn lại là 4m
Theo Pitago ta có: (8-x)2=x2+16
<=> 64-8x+x2=x2+16 <=> 8x=64-16 <=> 8x=48
=> x=6 (m)
Đáp số: Điểm gãy cách đất 6 (m)
Đúng 0
Bình luận (0)
Nhầm: 16x=48 => x=3
Điểm gãy cách đất 3 (m)
Đúng 0
Bình luận (0)
Một cây tre cao 9m bị gió bão làm gãy ngang thân, ngọn cây chạm đất cách gốc 3m . Hỏi điểm gãy cách gốc bao nhiêu?
A. 6m
B. 5m
C. 4m
D. 3m
Một cây tre cao 9m bị gió bão làm gãy ngang thân, ngọn cây chạm đất cách gốc 3m . Hỏi điểm gãy cách gốc bao nhiêu?
A. 6m
B. 5m
C. 4m
D. 3m