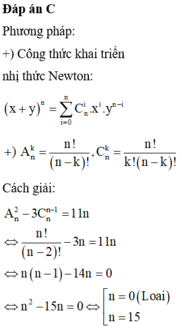Xét khai triển:

\(\left(1+2x\right)^{2n+1}=C_{2n+1}^0+C_{2n+1}^1.2x+C_{2n+1}^2\left(2x\right)^2+...+C_{2n+1}^{2n+1}\left(2x\right)^{2n+1}\)

Đạo hàm 2 vế:

\(2\left(2n+1\right)\left(1+2x\right)^{2n}=2C_{2n+1}^1+2^2C_{2n+1}^2x+...+\left(2n+1\right)2^{2n+1}C_{2n+1}^{2n+1}x^{2n}\)

\(\Leftrightarrow\left(2n+1\right)\left(1+2x\right)^{2n}=C_{2n+1}^1+2C_{2n+1}^2x+...+\left(2n+1\right)2^{2n}C_{2n+1}^{2n+1}x^{2n}\)

Cho \(x=-1\) ta được:

\(2n+1=C_{2n+1}^1-2C_{2n+1}^2+...+\left(2n+1\right)2^{2n}C_{2n+1}^{2n+1}\)

\(\Rightarrow2n+1=2019\Rightarrow n=1009\)

Ta có : \(C^k_{2n+1}=C^{2n+1-k}_{2n+1}\)

\(\Rightarrow2VT=C^1_{2n+1}+C^2_{2n+1}+...+C^{2n}_{2n+1}=2^{21}-2\)

\(\Leftrightarrow2^{2n+1}-C^0_{2n+1}-C^{2n+1}_{2n+1}=2^{21}-2\)

\(\Leftrightarrow2n+1=21\Leftrightarrow n=10\)

\(\sum\limits^{2n+1}_{k=0}C^k_{2n+1}=\left(1+1\right)^{2n+1}=2^{2n+1}\)

Lại có \(C^0_{2n+1}+C^1_{2n+1}+...+C^n_{2n+1}=C^{2n+1}_{2n+1}+C^{2n}_{2n+1}+...+C^{n+1}_{2n+1}\)

\(\Rightarrow C^0_{2n+1}+C^1_{2n+1}+...C^n_{2n+1}=\dfrac{2^{2n+1}}{2}\)

\(\Leftrightarrow2^{20}-1=2^{2n}-C^0_{2n+1}\)

\(\Leftrightarrow2^{20}-1=2^{2n}-1\)

\(\Leftrightarrow2n=20\)

\(\Leftrightarrow n=10\)

chỉ mk cách làm với @Nguyễn Việt Lâm

Xét khai triển:

\(\left(x+1\right)^{2n+1}=C_{2n+1}^0+C_{2n+1}^1x+C_{2n+1}^2x^2+...+C_{2n+1}^{2n+1}x^{2n+1}\)

Cho \(x=1\) ta được:

\(2^{2n+1}=C_{2n+1}^0+C_{2n+1}^1+C_{2n+1}^2+...+C_{2n+1}^{2n+1}\)

\(=1+C_{2n+1}^1+C_{2n+1}^2+...+C_{2n+1}^n+C_{2n+1}^{n+1}+...+C_{2n+1}^{2n}+1\)

\(=1+C_{2n+1}^1+...+C_{2n+1}^n+C_{2n+1}^n+...+C_{2n+1}^1+1\)

\(=2\left(1+C_{2n+1}^1+C_{2n+1}^2+...+C_{2n+1}^n\right)\)

\(\Rightarrow2^{2n}-1=C_{2n+1}^1+C_{2n+1}^2+...+C_{2n+1}^n\)

\(\Rightarrow2^{2n-1}=2^{20}-1\Rightarrow2n=20\Rightarrow n=10\)

Khai triển: \(\left(x^2-x-1\right)^{10}\)

\(\left\{{}\begin{matrix}k_0+k_1+k_2=10\\k_1+2k_2=6\end{matrix}\right.\) \(\Rightarrow\left(k_0;k_1;k_2\right)=\left(4;6;0\right);\left(5;4;1\right);\left(6;2;2\right);\left(7;0;3\right)\)

Hệ số của \(x^6:\)

\(\frac{10!}{4!.6!}+\frac{10!}{5!.4!}.\left(-1\right)^5+\frac{10!}{6!.2!.2!}+\frac{10!}{7!.3!}.\left(-1\right)^7\)

Giả thiết tương đương:

\(C_{2n+1}^{n+1}+C_{2n+1}^{n+2}+...+C_{2n+1}^{2n}+C_{2n+1}^{2n+1}=2^{100}\) (thay \(1=C_{2n+1}^{2n+1}\))

Mặt khác:

\(C_{2n+1}^{2n+1}=C_{2n+1}^0\)

\(C_{2n+1}^{2n}=C_{2n+1}^1\)

....

\(C_{2n+1}^{n+1}=C_{2n+1}^n\)

Cộng vế:

\(\Rightarrow C_{2n+1}^{n+1}+C_{2n+1}^{n+2}+...+C_{2n+1}^{2n+1}=C_{2n+1}^0+C_{2n+1}^1+...+C_{2n+1}^n\)

\(\Rightarrow2\left(C_{2n+1}^{n+1}+...+C_{2n+1}^{2n+1}\right)=C_{2n+1}^0+C_{2n+1}^1+...+C_{2n+1}^{2n+1}\)

\(\Rightarrow2.2^{100}=2^{2n+1}\) (đẳng thức cơ bản: \(\sum\limits^n_{k=0}C_n^k=2^n\))

\(\Leftrightarrow2^{101}=2^{2n+1}\)

\(\Rightarrow2n+1=101\)

\(\Rightarrow n=50\)

SHTQ trong khai triển: \(C_{50}^k.\left(x^{-3}\right)^k.\left(x^2\right)^{50-k}=C_{50}^kx^{100-5k}\)

\(100-5k=20\Rightarrow k=16\)

Hệ số: \(C_{50}^{16}\)

sao lại C^3_2n+1 nhỉ

ta có \(\left(1+1\right)^{2n+1}=C_{2n+1}^0+C^1_{2n+1}+C^2_{2n+1}+...+C^{2n+1}_{2n+1}\)

\(-\left(1-1\right)^{2n+1}=-\left(C_{2n+1}^0-C^1_{2n+1}+C^2_{2n+1}-...-C^{2n+1}_{2n+1}\right)\)

\(\left(1+1\right)^{2n+1}-\left(1-1\right)^{2n+1}=C_{2n+1}^0+C^1_{2n+1}+C^2_{2n+1}+...+C^{2n+1}_{2n+1}-C_{2n+1}^0+C_{2n+1}^1-C_{2n+1}^2+....+C_{2n+1}^{2n+1}\)

\(2^{2n+1}=2C_{2n+1}^1+2C_{2n+1}^3+2C_{2n+1}^5+...+C_{2n+1}^{2n+1}=2.1024=2048\)

\(\Rightarrow n=5\)

\(\left(2-3x\right)^{10}\)

SHTQ \(C_{10}^k.2^{10-k}.\left(-3x\right)^k=C_{10}^k.2^{10-k}.-3^k.x^k\)

\(x^7\Rightarrow k=7\)

hệ số cần tìm \(C_{10}^7.2^3.\left(-3\right)^7=-2099520\)

Câu 2 đề thiếu rồi kìa. Cái cuối cùng là tổ hợp chập bao nhiêu của 2n + 1 thế???

1/ Vì M thuộc \(d_3\) nên ta có tọa độ của M là: \(M\left(2a;a\right)\)

Khoản cách từ M đến \(d_1\) là:

\(d\left(M,d_1\right)=\dfrac{\left|2a+a+3\right|}{\sqrt{1^2+1^2}}=\dfrac{\left|3a+3\right|}{\sqrt{2}}\)

Khoản cách từ M đến \(d_2\) là:

\(d\left(M,d_2\right)=\dfrac{\left|2a-a-4\right|}{\sqrt{1^2+1^2}}=\dfrac{\left|a-4\right|}{\sqrt{2}}\)

Theo đề bài ta có:

\(\dfrac{\left|3a+3\right|}{\sqrt{2}}=2.\dfrac{\left|a-4\right|}{\sqrt{2}}\)

\(\Leftrightarrow\left|3a+3\right|=2.\left|a-4\right|\)

\(\Leftrightarrow a^2+10a-11=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=1\\a=-11\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}M\left(2;1\right)\\M\left(-22;-11\right)\end{matrix}\right.\)

2/ Ta có:

\(C_{2n+1}^1+C_{2n+2}^2+...+C_{2n+1}^n=2^{20}-1\)

\(\Leftrightarrow2\left(C_{2n+1}^0+C_{2n+1}^1+C_{2n+2}^2+...+C_{2n+1}\right)^n=2^{21}\)

\(\Leftrightarrow C_{2n+1}^0+C_{2n+1}^1+C_{2n+2}^2+...+C_{2n+1}^n+...+C_{2n+1}^{2n+1}=2^{21}\)

\(\Leftrightarrow2^{2n+1}=2^{21}\)

\(\Leftrightarrow n=10\)

Ta có số hạng tổng quát trong khai triển của \(\left(\dfrac{1}{x^4}+x^7\right)^{10}\) là:

\(C_{10}^k.\left(\dfrac{1}{x^4}\right)^{10-k}.\left(x^7\right)^k=C_{10}^k.x^{11k-40}\)

Để số hạng chứa \(x^{26}\) thì \(11k-40=26\)

\(\Leftrightarrow k=6\)

Vậy hệ số cần tìm là: \(C_{10}^6\)

1=(2n+1)C0, (2n+1)Cn=(2n+1)C(n+1)...