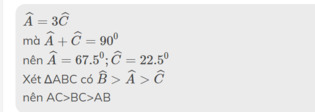Cho tam giác ABC có A-B-C=90 độ và A-C=5 độ .So sánh cạnh của tam giác ABC

Những câu hỏi liên quan
bài 1: cho tam giác ABC có A-B+C= 90 độ và A-C=-5 độ .So sánh cạnh trong tam giác ABC
Xem chi tiết
bài 2:cho tam giác ABC có A+B-2C=27 độ và A+3C=273 độ.So sánh các cạnh trong tam giác ABC
bài 3:cho tam giác ABC có C-3B-2A=-3 độ và 5B-2A=16 độ. Tính các góc từ đó so sánh các cạnh trong tam giác ABC
cho tam giác ABC có ^B=90 độ biết ^A=3 ^c so sánh 3 cạnh của tam giác
cho tam giác ABC có ^B=90 độ biết ^A=3 ^c so sánh 3 cạnh của tam giác
\(\widehat{A}=3\widehat{C}\)
mà \(\widehat{A}+\widehat{C}=90^0\)
nên \(\widehat{A}=67.5^0;\widehat{C}=22.5^0\)
Xét ΔABC có \(\widehat{B}>\widehat{A}>\widehat{C}\)
nên AC>BC>AB
Đúng 0
Bình luận (0)
cho tam giác abc có góc a = 60 độ góc c < góc B < 90 độ
a, cm ab<ac
b cm trên cạnh ac lấy điểm m sao cho am = ab .Chứng minh tam giác abm là tam giác đều
c, so sánh các cạnh của tam giác abc
a: góc C<góc B
=>AB<AC
b: Xét ΔABM co AB=AM và góc A=60 độ
nên ΔAMB đều
Đúng 0
Bình luận (0)
cho tam giác ABC có góc A-góc B+góc C=90 độ và góc A-góc C=-5 độ.So sánh các cạnh trong tam giác
Đặt \(\widehat{A}=a;\widehat{B}=b;\widehat{C}=c\)
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>a+b+c=180(1)
\(\widehat{A}-\widehat{B}+\widehat{C}=90^0\)
=>a-b+c=90(2)
\(\widehat{A}-\widehat{C}=-5^0\)
=>\(\widehat{C}-\widehat{A}=5^0\)
=>c-a=5(3)
Từ (1),(2),(3) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b+c=180\\a-b+c=90\\c-a=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a+c+b=180\\a+c-b=90\\c-a=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+c=\dfrac{180+90}{2}=\dfrac{270}{2}=135\\b=\dfrac{180-90}{2}=\dfrac{90}{2}=45\\c-a=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=45\\c+a=135\\c-a=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=45\\c=\dfrac{135+5}{2}=\dfrac{140}{2}=70\\a=c-5=70-5=65\end{matrix}\right.\)
Vậy: \(\widehat{A}=65^0;\widehat{B}=45^0;\widehat{B}=70^0\)
Xét ΔABC có \(\widehat{B}< \widehat{A}< \widehat{C}\)
mà AC,BC,AB lần lượt là cạnh đối diện của các góc ABC;BAC;ACB
nên AC<BC<AB
Đúng 2
Bình luận (1)
Bài 2: Cho tam giác ABC có góc A90 độ , lấy điểm M thuộc cạnh AB .a) So sánh AC và MC b) Chứng minh tam giác MBC là tam giác tùc) Chứng minh AC MC BCBài 3: Cho tam giác MNP có Góc N90 độ , trên tia đối của tia NP lấy điểm Q .a) So sánh MN và MP b) Chứng minh tam giác MPQlà tam giác tù.c) Chứng minh MNMPMQBài 4: Cho tam giác ABC có AB3 cm, AC4 cma) So sánh góc B với gócCb) Hạ AH vuông góc với BC tại H . So sánh góc BAH và góc CAHBài 5: Cho tam giác ABC có AB 5 cm, AC 3 cma) So sánh góc B với gó...
Đọc tiếp
Bài 2: Cho tam giác ABC có góc A>90 độ , lấy điểm M thuộc cạnh AB .
a) So sánh AC và MC
b) Chứng minh tam giác MBC là tam giác tù
c) Chứng minh AC <MC <BC
Bài 3: Cho tam giác MNP có Góc N>90 độ , trên tia đối của tia NP lấy điểm Q .
a) So sánh MN và MP
b) Chứng minh tam giác MPQlà tam giác tù.
c) Chứng minh MN<MP<MQ
Bài 4: Cho tam giác ABC có AB=3 cm, AC=4 cm
a) So sánh góc B với gócC
b) Hạ AH vuông góc với BC tại H . So sánh góc BAH và góc CAH
Bài 5: Cho tam giác ABC có AB = 5 cm, AC = 3 cm
a) So sánh góc B với góc C
b) So sánh hai góc ngoài tại các đỉnh B và C của tam giác ABC
Bài 6: Cho tam giác ABC vuông tại A có AC=2AB . Lấy điểm E trên cạnh AC sao cho
AB=AE . Trên tia đối của tia EB lấy điểm D sao cho EB=ED
a) Chứng minh tam giác ABE= tam giác CDE
b) So sánh góc ABE và góc CBE
Bài 2 : Cho tam giác ABC có AB3cm; AC 4cm; BC 5cm . So sánh các góc của tam giác ABCBài 3 :Cho tam giác ABC có góc B60 độ ; góc C 40 độ . So sánh các cạnh của tam giác ABCBài 4 : Cho tam giác ABC có AB5cm ; AC 12 cm ; BC13 cma) Tam giác ABC là tam giác gì ?b) So sánh các góc của tam giác ABCBài 5 : Cho tam giác ABC vuông tại A có AB10cm ; AC 24 cma) Tính độ dài cạnh BC?b) Tam giác ABC là tam giác gì ?
Đọc tiếp
Bài 2 : Cho tam giác ABC có AB=3cm; AC= 4cm; BC= 5cm . So sánh các góc của tam giác ABC
Bài 3 :Cho tam giác ABC có góc B=60 độ ; góc C = 40 độ . So sánh các cạnh của tam giác ABC
Bài 4 : Cho tam giác ABC có AB=5cm ; AC= 12 cm ; BC=13 cm
a) Tam giác ABC là tam giác gì ?
b) So sánh các góc của tam giác ABC
Bài 5 : Cho tam giác ABC vuông tại A có AB=10cm ; AC= 24 cm
a) Tính độ dài cạnh BC=?
b) Tam giác ABC là tam giác gì ?
bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết
Đúng 0
Bình luận (0)
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC có : góc A= 90 độ, góc C = 75 độ
a) So sánh các cạnh của tam giác ABC
b)Gọi H là hình chiếu của điểm A trên cạnh BC. So sánh HB và HC
C,Vẽ trung tuyến BM và CN cắt nhau tại điểm G
Cho BG=9cm , GN=2cm. Tính GM và CN
a: Xét ΔABC có \(\widehat{B}< \widehat{C}< \widehat{A}\)
nên AC<AB<BC
b: Xét ΔABC có AB>AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB>HC
c: BG=2GM
nên GM=4,5(cm)
CN=3GN
nên CN=6(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC có A=2B và B+C=80 độ. Hãy so sánh các cạnh của tam giác ABC.