a) tự vẽ

b) Ta có phương trình hoành độ giao điểm của đồ thị hàm số (P) và đường thẳng (d) là:

 2x² = x + 3

<=> 2x² - x - 3 = 0

Do a - b + c = 2 + 1 - 3 = 0 

=> phương trình có 2 nghiệm phân biệt x1 = -1; x2 = 3/2

Với x = -1 => y = -1 + 3 = 2 => tọa độ giao điểm là (-1;2)

x = 3/2 => y = 3/2 + 3 = 9/2 => tọa độ giao điểm là (3/2; 9/2)

a)

\(\left(P\right):y=x^2\)

Ta có bảng

Vậy đồ thị hàm số \(y=x^2\) là một parabol lần lượt đi qua các điểm 

\(\left(-2;4\right),\left(-1;1\right),\left(0;0\right),\left(1;1\right),\left(2;4\right)\)

Bạn tự vẽ nhé

\(\left(d\right):y=-2x+3\)

Cho \(y=0\Rightarrow x=\dfrac{3}{2}\Rightarrow A\left(\dfrac{3}{2};0\right)\in Ox\)

Cho \(x=0\Rightarrow y=3\Rightarrow B\left(0;3\right)\in Oy\)

Vẽ đường thẳng AB ta được đths \(y=-2x+3\)

Bạn tự bổ sung vào hình vẽ nhé

b) Xét PTHĐGĐ của \(\left(P\right),\left(d\right)\) là nghiệm của phương trình

\(x^2=-2x+3\\ \Leftrightarrow x^2+2x-3=0\)

Xét \(a+b+c=1+2-3=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)

Với `x=1 => y=x^2 = 1`

Với `x=2 => y=x^2 = 4`

Vậy tọa độ giao điểm của \(\left(P\right),\left(d\right)\) là 2 điểm \(\left(1;1\right)\) và \(\left(2;4\right)\)

b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)

hay \(-x-4=3x+2\)

\(\Leftrightarrow-x-4-3x-2=0\)

\(\Leftrightarrow-4x-6=0\)

\(\Leftrightarrow-4x=6\)

hay \(x=-\dfrac{3}{2}\)

Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được: 

\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)

Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)

c) Vì (D2) song song với (D) nên a=-1

hay (D2): y=-x+b

Vì (D2) đi qua điểm B(-2;5)

nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được: 

-(-2)+b=5

hay b=5-2=3

Vậy: (D2): y=-x+3

b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)

hay \(-x-4=3x+2\)

\(\Leftrightarrow-x-4-3x-2=0\)

\(\Leftrightarrow-4x-6=0\)

\(\Leftrightarrow-4x=6\)

hay \(x=-\dfrac{3}{2}\)

Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được: 

\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)

Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)

c) Vì (D2) song song với (D) nên a=-1

hay (D2): y=-x+b

Vì (D2) đi qua điểm B(-2;5)

nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được: 

-(-2)+b=5

hay b=5-2=3

Vậy: (D2): y=-x+3

b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)

hay \(-x-4=3x+2\)

\(\Leftrightarrow-x-4-3x-2=0\)

\(\Leftrightarrow-4x-6=0\)

\(\Leftrightarrow-4x=6\)

hay \(x=-\dfrac{3}{2}\)

Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được: 

\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)

Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)

c) Vì (D2) song song với (D) nên a=-1

hay (D2): y=-x+b

Vì (D2) đi qua điểm B(-2;5)

nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được: 

-(-2)+b=5

hay b=5-2=3

Vậy: (D2): y=-x+3

a: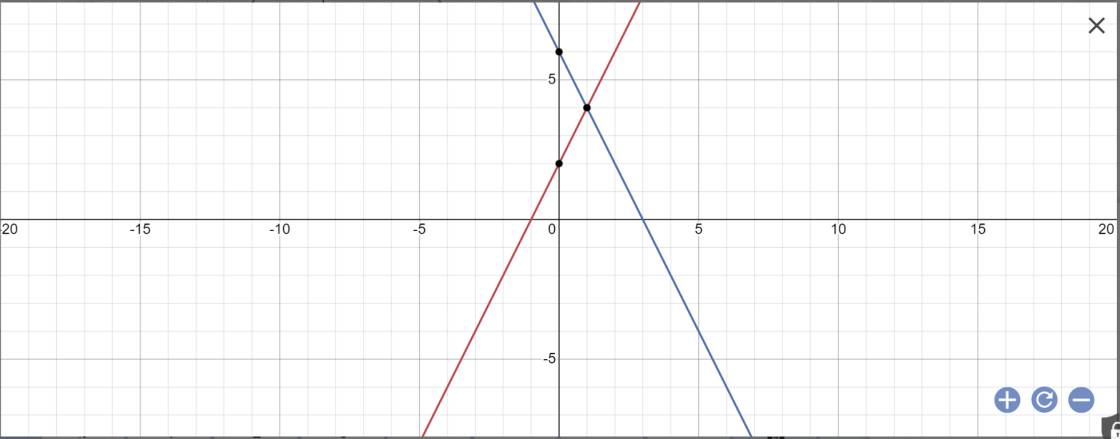 

b: Phương trình hoành độ giao điểm là:

2x+2=6-2x

=>2x+2x=6-2

=>4x=4

=>x=1

Thay x=1 vào y=2x+2, ta được:

\(y=2\cdot1+2=4\)

Vậy: (d1) cắt (d2) tại A(1;4)

c: Thay x=0 vào y=x-6, ta được:

y=0-6=-6

Thay x=0 và y=-6 vào y=ax+b, ta được:

\(a\cdot0+b=-6\)

=>b=-6

=>y=ax-6

Thay x=2 vào y=2x+1, ta được:

\(y=2\cdot2+1=5\)

Thay x=2 và y=5 vào y=ax-6, ta được:

2a-6=5

=>2a=11

=>\(a=\dfrac{11}{2}\)

c: Vì (d2)//(d) nên \(a=-\dfrac{1}{2}\)

Thay x=-3 và y=0 vào \(y=\dfrac{-1}{2}x+b\), ta được:

\(b+\dfrac{3}{2}=0\)

hay \(b=-\dfrac{3}{2}\)