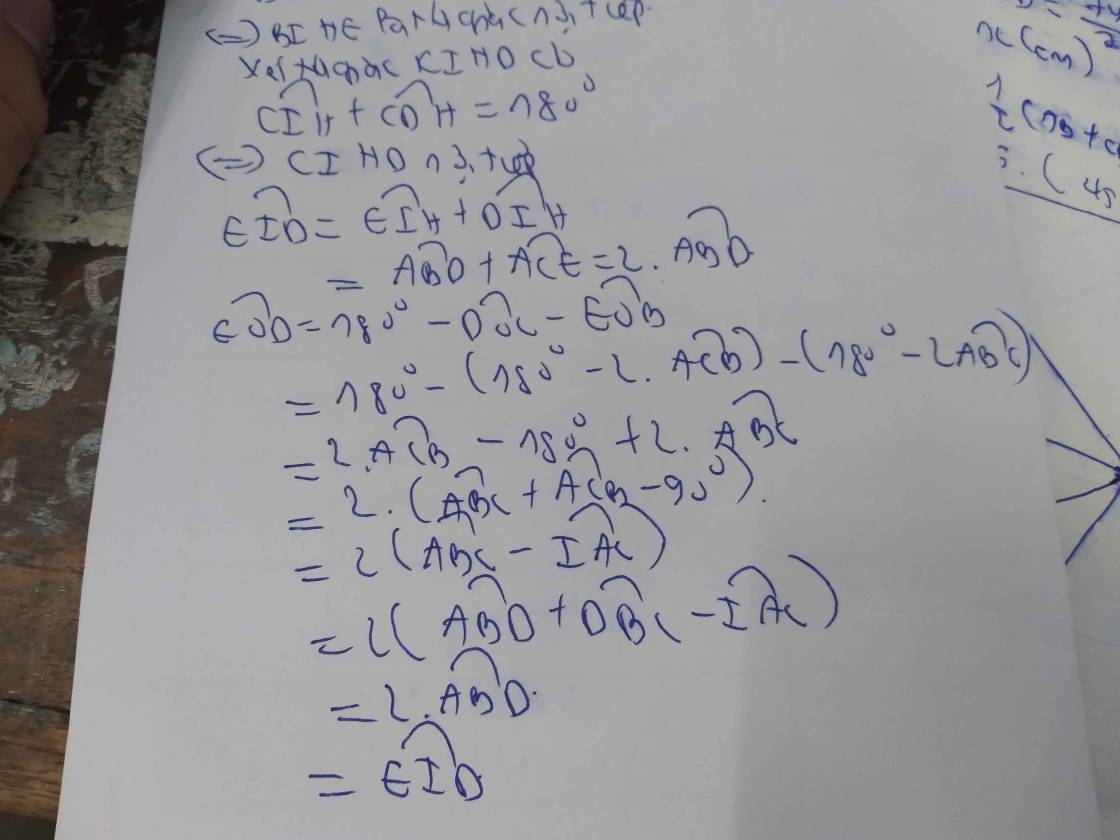Giúp mình câu c với gợi ý là gọi S là giao điểm của PF và CD rồi chứng minh tam giác OSP cân tại O.
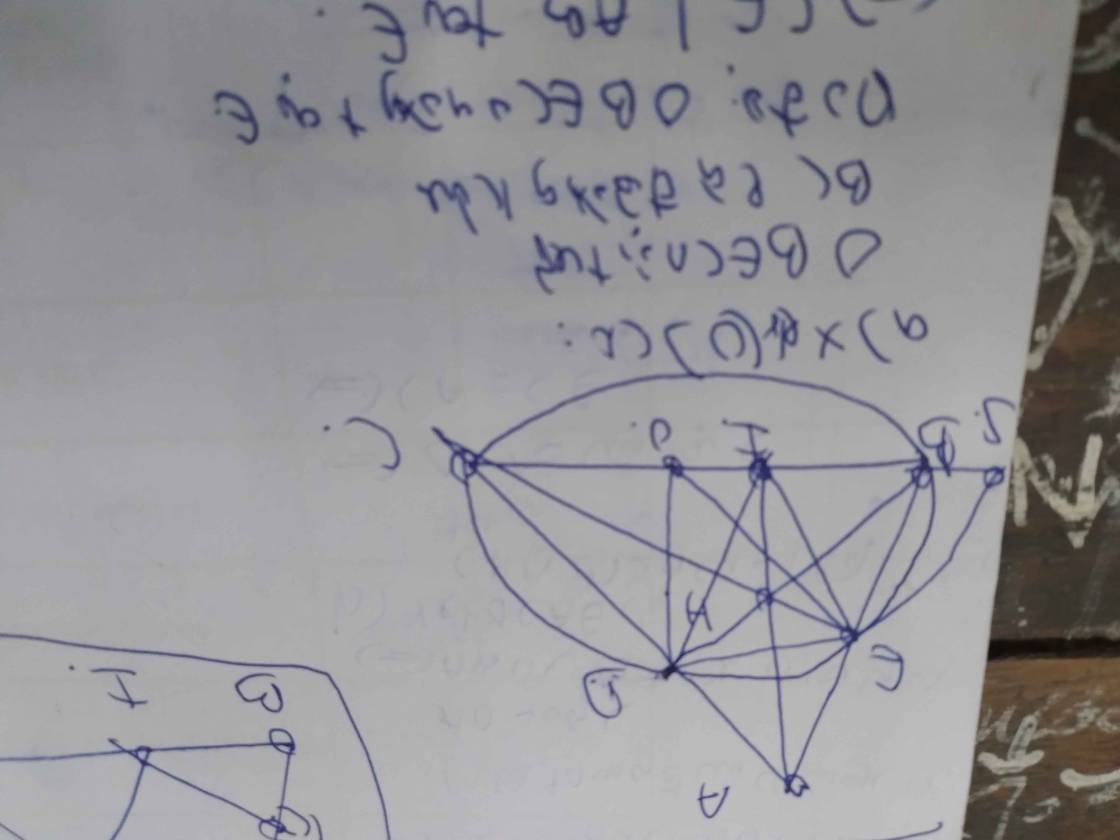
Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O;R). Hai đường cao AF và BE cắt nhau tại H. Kẻ đường kính AK của (O). Tia AF cắt (O) tại D
a) Chứng minh : AB.AC = AF.AK và F là trung điểm của HD b) Giả sử BC = R căn 3. Tính AB.CK + AC.BK theo R c) Qua F vẽ đường thẳng vuông góc với OF cắt cạnh AB tại P. Chứng minh góc PHF = góc ABC.
Hai vòi nước chảy vào 1 bể thì đầy bể trong 3 giờ 20 phút . Người ta cho vòi thứ nhất chảy 3 giờ , vòi thứ 2 chảy 2 giờ thì cả hai vòi chảy được 4/5 bể . Tính thời gian mỗi vòi chảy một mình đẩy bể .