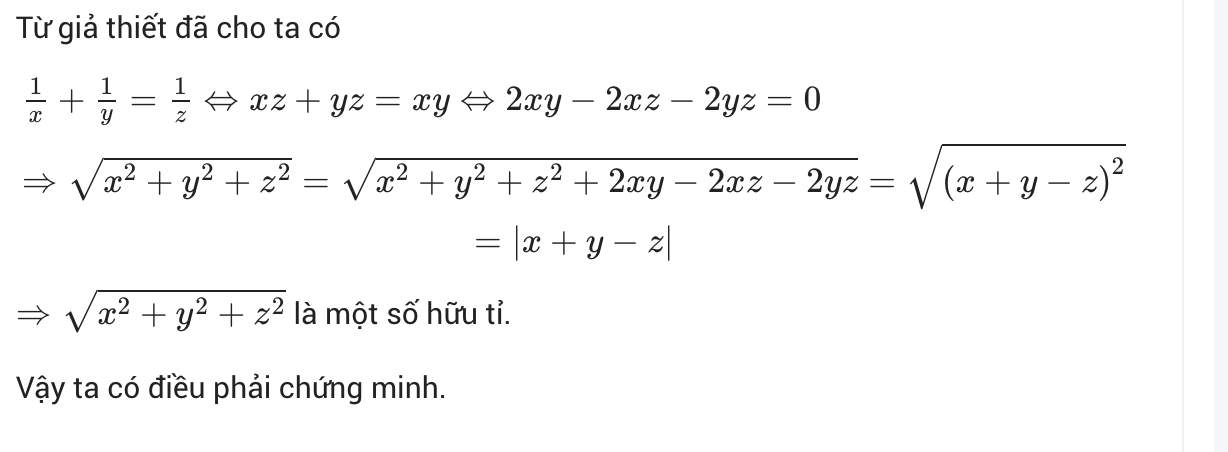Tham khảo nha ông:

A=\(\frac{x^2y^2+x^2z^2+y^2z^2}{x^2y^2z^2}\)

Ta có:\(x^2y^2+x^2z^2+y^2z^2=\left(xy+yz+zx\right)^2-2\left(xyz\right)\left(x+y+z\right)\)

\(=\left(xy+yz+zx\right)^2\)(do x+y+z=0)

Do đó A=\(\frac{\left(xy+yz+zx\right)^2}{\left(xyz\right)^2}=\left[\frac{\left(xy+yz+zx\right)}{xyz}\right]^2\)

Nên A là số chính phương(ĐCCM)

Ta có:

\(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+0}=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2\left(x+y+z\right)}{xyz}}\)

\(=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2}{xy}+\dfrac{2}{yz}+\dfrac{2}{zx}}=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2}\)

\(=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\) là số hữu tỉ

x(x+y+z) + y(x+y+z) + z(x+y+z)= 4+6+6

(x+y+z)(x+y+z)=16

(x+y+z)^2=16 => x+y+z=4 hoặc -4

nếu x+y+z=4 thì:

x(x+y+z)=4                 y(x+y+z)=z(x+y+z)=6

x.4=4 => x=1              y.4=z.4=6 =>y=z=1,5

nếu x+y+z=-4 thì:

x(x+y+z)=4                 y(x+y+z)=z(x+y+z)=6

x.(-4)=4 =>x=-1            y.(-4)=z(-4)= 6=> y=z=-1,5

Ta có: x(x+y+z) = 4

          y(x+y+z) = 6

          z(x+y+z) = 6

Cộng vế theo vế, ta được (x+y+z)² = 16 => x+y+z = 4 hoặc -4

Ta có 2 trường hợp sau: 

TH 1: x+y+z = 4

Mà x(x+y+z) = 4 => x = 1

y(x+y+z) = 6 => y = 6/4 = 3/2

                    => z = 3/2

TH 2: x+y+z = -4

Mà x(x+y+z) = -4 => x = -1

y(x+y+z) = 6 => y = -6/4=-3/2

                   => z = -3/2

Vậy ta có tất cả là 2 cặp số hữu tỉ thỏa mãn đầu bài 

chỉ có 2 cặp thui nha

Ta có: \(\hept{\begin{cases}|x+2y-z|\ge0;\forall x,y,z\\\left(x-y+3z\right)^2\ge0;\forall x,y,z\\\left(z-1\right)^4\ge0;\forall x,y,z\end{cases}}\)\(\Rightarrow|x+2y-z|+\left(x-y+3z\right)^2+\left(z-1\right)^4\ge0;\forall x,y,z\)

Do đó \(|x+2y-z|+\left(x-y+3z\right)^2+\left(z-1\right)^4=0\)

\(\Leftrightarrow\hept{\begin{cases}|x+2y-z|=0\\\left(x-y+3z\right)^2=0\\\left(z-1\right)^4=0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x+2y-z=0\\x-y+3z=0\\z=1\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x+2y=1\\x-y=-3\\z=1\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x=\frac{-5}{3}\\y=\frac{4}{3}\\z=1\end{cases}}\)

Vậy ...

1/ a/ x = 1/2, y = -1

b/ x = -1/2 ; y = 1

Ta có: \(x+y=z\Rightarrow x=z-y\)

\(A=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}=\sqrt{\dfrac{x^2y^2+y^2z^2+x^2z^2}{x^2y^2z^2}}\)

\(=\sqrt{\dfrac{\left(z-y\right)^2y^2+y^2z^2+\left(z-y\right)^2z^2}{x^2y^2z^2}}\)

\(=\sqrt{\dfrac{y^4+y^2z^2-2y^3z+y^2z^2+z^4+y^2z^2-2yz^3}{x^2y^2z^2}}\)

\(=\sqrt{\dfrac{\left(y^4+2y^2z^2+z^4\right)-2yz\left(y^2+z^2\right)+y^2z^2}{x^2y^2z^2}}\)

\(=\sqrt{\dfrac{\left(y^2+z^2\right)^2-2yz\left(y^2+z^2\right)+y^2z^2}{x^2y^2z^2}}\)

\(=\sqrt{\dfrac{\left(y^2+z^2-yz\right)^2}{x^2y^2z^2}}=\left|\dfrac{y^2+z^2-yz}{xyz}\right|\)

Là một số hữu tỉ do x,y,z là số hữu tỉ