Cho Tam Giác ABC , AB = 4,5cm . AC = 6cm , BC = 7,5cm . Đo Góc A Rút ra nhận xét
GIÚP MIK VỚI
Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm. Chứng minh tam giác ABC vuông ở A. Tính các góc B , C và đường cao AH của tam giác
Ta có:
A B 2 = 6 2 = 36 A C 2 = 4 , 52 = 20 , 25 B C 2 = 7 , 52 = 56 , 25
Vì A B 2 + A C 2 = 36 + 20,25 = 56,25 = B C 2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
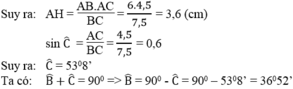
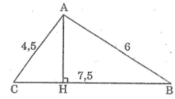
Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.
Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.
Ta có: AB2 + AC2 = 62 + 4,52 = 7,52 = BC2
nên tam giác ABC vuông tại A. (đpcm)
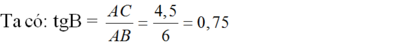
=> ∠B = 37o
=> ∠C = 90o - ∠B = 90o - 37o = 53o
Mặt khác trong tam giác ABC vuông tại A, ta có:
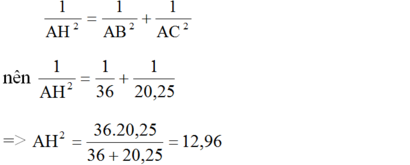
=> AH = 3,6 cm
Cho tam giác vuông ABC có hai cạnh góc vuông AB = 4,5cm, AC= 6cm, cạnh huyền BC = 7,5cm. Tính chiều cao AH của hình tam giác vuông ABC.
TK
Diện tích tam giác là:
(4,5 x 6)/2=13,5 cm
Chiều cao AH là:
(13,5 x 2)/7,5=3,6 cm
Cho tam giác vuông ABC có hai cạnh góc vuông AB = 4,5cm, AC = 6cm. Cạnh huyền BC = 7,5cm. Tính chiều cao AH của hình tam giác ABC
Giải
Độ dài chiều cao AH là :
( 4,5 + 6 ) : 2 = 5,25 ( cm )
Đáp số : 5,25 cm
Mong bạn k mk
yến nhi libra virgo hotgirl sakura trả lời chính xác
quá đúng...!!
tk mk nha
thanks
độ dài chiều cao AH là
(4,5+6);2=5,25 (cm)
đáp số: 5,25cm
_ các bạn thấy mk làm đúng thì
THANKS CÁC BẠN NHIU
Cho tam giác ABC có AB= 4,5cm; BC= 6cm; AC= 7,5cm. Chứng minh tam giác ABC là tam giác vuông
Áp dụng ĐL pi - ta - go đảo :
\(AB^2+BC^2=AC^2\)
\(< =>4.5^2+6^2=7.5^2\)
Do \(4.5^2+6^2=7.5^2\)đúng
=>ĐPCM
Tam giác ABC, AB= 4,5cm, AC= 6cm, BC=7,5cm. Phân giác BD của góc B cắt AC ở D. Tính tỉ số lượng giác của góc ABD.
Ta có:
7.5^2=4.5^2+6^2
→BC2=AB2+AC2
→ΔABC vuông tại A
Ta có BD là phân giác góc B→DA/DC=BA/BC=35
→DA/DA+DC=3/3+5
→AD/AC=38
→AD=3/8AC=94
→BD=√AB2+AD2=9√54→BD=AB2+AD2=954
→sinˆABD=ADBD=1√5→sinABD^=ADBD=15
cosˆABD=ABBD=2√5cosABD^=ABBD=25
tanˆABD=sinˆABDcosˆABD=12tanABD^=sinABD^cosABD^=12
cotˆABD=1tanˆABD=2

Cho tam giác ABC biết BC = 7,5cm, AC = 4,5cm, AB = 6cm
a, Tính đường cao AH của tam giác ABC
b, Tính độ dài BH, CH
Cho tấm giác ABC biết BC=7,5cm; AC= 4,5cm ;AB= 6cm a) Tính đường cao AH của tam giác ABC b) Tính BH và CH
a: Xét ΔABC có \(BC^2=AC^2+AB^2\)
nên ΔABC vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot7.5=4.5\cdot6=27\)
hay AH=3,6(cm)
b:
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}BH\cdot BC=AB^2\\CH\cdot BC=AC^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=4,8\left(cm\right)\\CH=2,7\left(cm\right)\end{matrix}\right.\)
có AB2+AC2=4,52+62=56,25=7,52
tam giác abc vuông tại a
=> AH.BC=AB.AC
AH.7,5=4,5.6
AH.7,5=27
AH= 3,6
a) Ta có: 4,5\(^2\) + 6\(^2\) = 56,25 ; 7,5\(^2\) = 56,25
⇒ AB\(^2\) + AC\(^2\) = BC\(^2\)
Vậy △ ABC vuông tại A
Áp dụng hệ thức lượng ta có:
AB . AC = AH . BC
⇒ AH = \(\dfrac{\left(AB.AC\right)}{BC}\) = 3,6
b) Áp dụng hệ thức lượng ta có:
AB2 = BH . BC
⇒ BH = \(\dfrac{AB^2}{BC}\) = 4,8
⇒ CH = BC - BH = 2,7
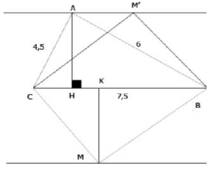
Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm. Tìm tập hợp các điểm M sao cho S A B C = S B M C
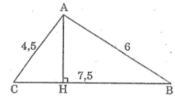
Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời S A B C = S B M C nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.