a: Ta có: \(3x-5\ge2\left(x-6\right)-12\)

\(\Leftrightarrow3x-5\ge2x-24\)

hay \(x\ge-19\)

b: Ta có: \(2\left(5-2x\right)\ge3-x\)

\(\Leftrightarrow10-4x-3+x\ge0\)

\(\Leftrightarrow-3x\ge-7\)

hay \(x\le\dfrac{7}{3}\)

a: Ta có: \(3x+5\le4x-9\)

\(\Leftrightarrow-x\le-14\)

\(\Leftrightarrow x\ge14\)

b: Ta có: \(6-2x< 6-x\)

\(\Leftrightarrow-x< 0\)

hay x>0

c: Ta có: \(7\left(x-1\right)+5>-3x\)

\(\Leftrightarrow7x-7+5+3x>0\)

\(\Leftrightarrow10x>2\)

hay \(x>\dfrac{1}{5}\)

\(\dfrac{x}{2x-6}-\dfrac{x}{2x+2}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\left(ĐKXĐ:x\ne-1,x\ne3\right)\)

\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}-\dfrac{x}{2\left(x+1\right)}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)

\(\Leftrightarrow\dfrac{x\left(x+1\right)}{2\left(x+1\right)\left(x-3\right)}-\dfrac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{2x\cdot2}{2\left(x+1\right)\left(x-3\right)}\)

\(\Rightarrow x\left(x+1\right)-x\left(x-3\right)=4x\)

\(\Leftrightarrow x^2+x-x^2+3x=4x\)

\(\Leftrightarrow x^2+x-x^2+3x-4x=0\)

\(\Leftrightarrow0x=0\)

Phương trình có vô số nghiệm , trừ x = -1,x = 3

Vậy ...

\(\dfrac{12x+1}{12}< \dfrac{9x+1}{3}-\dfrac{8x+1}{4}\)

\(\Leftrightarrow12\cdot\dfrac{12x+1}{12}< 12\cdot\dfrac{9x+1}{3}-12\cdot\dfrac{8x+1}{4}\)

\(\Leftrightarrow12x+1< 4\left(9x+1\right)-3\left(8x+1\right)\)

\(\Leftrightarrow12x+1< 36x+4-24x-3\)

\(\Leftrightarrow12x+1< 12x+1\)

\(\Leftrightarrow12x-12x< 1-1\)

\(\Leftrightarrow0x< 0\)

Vậy S = {x | x \(\in R\)}

4: =>2x-3>5 hoặc 2x-3<-5

=>x>4 hoặc x<-1

5: =>-4<=2x-1<=4

=>-3/2<=x<=5/2

a.

\(3\sqrt{-x^2+x+6}\ge2\left(1-2x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-x^2+x+6\ge0\\1-2x< 0\end{matrix}\right.\\\left\{{}\begin{matrix}1-2x\ge0\\9\left(-x^2+x+6\right)\ge4\left(1-2x\right)^2\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-2\le x\le3\\x>\dfrac{1}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\25\left(x^2-x-2\right)\le0\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}< x\le3\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\-1\le x\le2\end{matrix}\right.\end{matrix}\right.\)

\(\Rightarrow-1\le x\le3\)

b.

ĐKXĐ: \(x\ge0\)

\(\Leftrightarrow\sqrt{2x^2+8x+5}-4\sqrt{x}+\sqrt{2x^2-4x+5}-2\sqrt{x}=0\)

\(\Leftrightarrow\dfrac{2x^2+8x+5-16x}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-4x+5-4x}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)

\(\Leftrightarrow\dfrac{2x^2-8x+5}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-8x+5}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)

\(\Leftrightarrow\left(2x^2-8x+5\right)\left(\dfrac{1}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{1}{\sqrt{2x^2-4x+5}+2\sqrt{x}}\right)=0\)

\(\Leftrightarrow2x^2-8x+5=0\)

\(\Leftrightarrow x=\dfrac{4\pm\sqrt{6}}{2}\)

Câu b còn 1 cách giải nữa:

Với \(x=0\) không phải nghiệm

Với \(x>0\) , chia 2 vế cho \(\sqrt{x}\) ta được:

\(\sqrt{2x+8+\dfrac{5}{x}}+\sqrt{2x-4+\dfrac{5}{x}}=6\)

Đặt \(\sqrt{2x-4+\dfrac{5}{x}}=t>0\Leftrightarrow2x+8+\dfrac{5}{x}=t^2+12\)

Phương trình trở thành:

\(\sqrt{t^2+12}+t=6\)

\(\Leftrightarrow\sqrt{t^2+12}=6-t\)

\(\Leftrightarrow\left\{{}\begin{matrix}6-t\ge0\\t^2+12=\left(6-t\right)^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}t\le6\\12t=24\end{matrix}\right.\)

\(\Rightarrow t=2\)

\(\Rightarrow\sqrt{2x-4+\dfrac{5}{x}}=2\)

\(\Leftrightarrow2x-4+\dfrac{5}{x}=4\)

\(\Rightarrow2x^2-8x+5=0\)

\(\Leftrightarrow...\)

\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)

\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)

Bảng xét dấu:

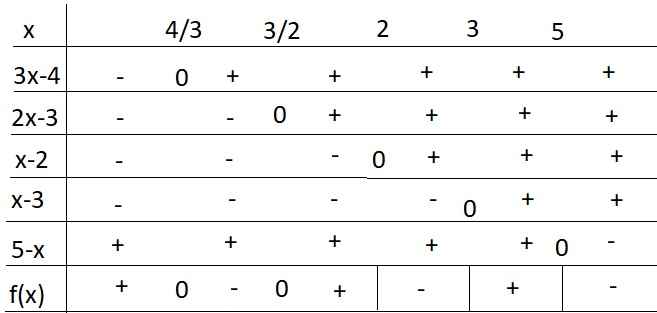
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)

\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)

\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)

\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)

\(\Leftrightarrow x^2-9-x^2+3x=0\)

\(\Leftrightarrow3x-9=0\)

\(\Leftrightarrow3x=9\)

\(\Leftrightarrow x=3\left(n\right)\)

Vậy \(S=\left\{3\right\}\)

\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)

\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)

\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)

\(\Leftrightarrow12x-9-12x+20+2x-7>0\)

\(\Leftrightarrow2x+4>0\)

\(\Leftrightarrow2x>-4\)

\(\Leftrightarrow x>-2\)

1:

a: =>3x=6

=>x=2

b: =>4x=16

=>x=4

c: =>4x-6=9-x

=>5x=15

=>x=3

d: =>7x-12=x+6

=>6x=18

=>x=3

2:

a: =>2x<=-8

=>x<=-4

b: =>x+5<0

=>x<-5

c: =>2x>8

=>x>4

1.

\(6+2x\ge3-x\)

\(\Leftrightarrow3x\ge-3\)

\(\Leftrightarrow x\ge-1\)

2.

\(2x+7>16-x\)

\(\Leftrightarrow3x>23\)

\(\Leftrightarrow x>\dfrac{23}{3}\)

3.

\(x-5< 3x+1\)

\(\Leftrightarrow2x>-6\)

\(\Leftrightarrow x>-3\)

Mik chưa học đến lớp 8 nên ko bt biểu diễn trên trục số nên chỉ tìm dc x thôi nha:

1. 6 + 2x \(\ge\) 3 - x

<=> 6 - 3 \(\ge\) -x - 2x

<=> 3 \(\ge\) -3x

<=> 3 : (-3) \(\ge\) -3x : (-3)

<=> -1 \(\le\) x

<=> x \(\ge\) -1

2. 2x + 7 > 16 - x

<=> 2x + x > 16 - 7

<=> 3x > 9

<=> 3x : 3 > 9 : 3

<=> x > 3

3. x - 5 < 3x + 1

<=> -5 - 1 < 3x - x

<=> -6 < 2x

<=> -6 : 2 < 2x : 2

<=> -3 < x

<=> x > (-3)

1: Ta có: \(2x+6\ge3-x\)

\(\Leftrightarrow3x\ge-3\)

hay \(x\ge-1\)

2: ta có: \(2x+7>16-x\)

\(\Leftrightarrow3x>9\)

hay x>3

3: Ta có: \(x-5< 3x+1\)

\(\Leftrightarrow-2x< 6\)

hay x>-3

`(x-3)/5+1<2x-5`

`<=>x-3+5<5(2x-5)`

`<=>x+2<10x-25`

`<=>8x>27`

`<=>x>27/8`

Vậy `S={x|x>27/8}`

bạn ơi đề là như 1 hay 2 ạ??