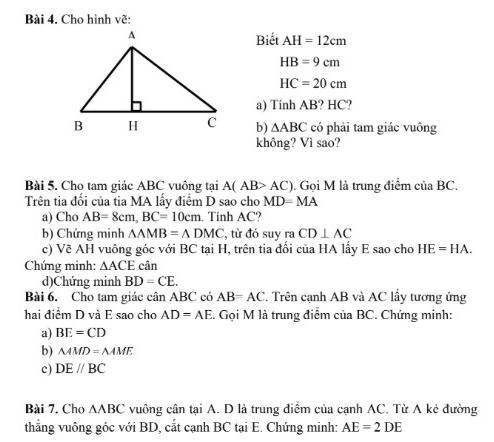
cho tam giác ABC vuông cân tại A , D là trung điểm của cạnh AC . từ A kẻ đường thẳng vuông góc với BD cắt cạnh BC tại E a, chứng minh AE = 2 DE
Làm theo cach lớp 7 nhé
cho tam giác ABC vuông cân tại A , D là trung điểm của cạnh AC . từ A kẻ đường thẳng vuông góc với BD cắt cạnh BC tại E
a, chứng minh AE = 2 DE
Làm theo cách lớp 7 nhé
Câu hỏi của Lương Thu Trang - Toán lớp 7 - Học toán với OnlineMath
cho tam giác ABC vuông cân tại A , D là trung điểm của cạnh AC . từ A kẻ đường thẳng vuông góc với BD cắt cạnh BC tại E
a, chứng minh AE = 2 DE
Làm theo cách lớp 7 nhé !
Đó là cách lớp 8 rồi bn
Câu hỏi của Lương Thu Trang - Toán lớp 7 - Học toán với OnlineMath
cho tam giác ABC vuông cân tại A , D là trung điểm của cạnh AC . từ A kẻ đường thẳng vuông góc với BD cắt cạnh BC tại E
a, chứng minh AE = 2 DE
LÀM THEO CÁCH LỚP 7 NHÉ !!!
HELP ME TT
Đó là cách lớp 8 rồi mà
Cho tam giác ABC vuông cân tại A, D là trung điểm của cạnh AC. Từ A kẻ đường thẳng vuông góc với BD, cắt cạnh BC tại E. Chứng minh AE = 2DE.
Cho tam giác ABC vuông cân tại A, D là trung điểm của cạnh AC. Từ A kẻ đường thẳng vuông góc với BD, cắt cạnh BC tại E. Chứng minh AE = 2DE
Bài 7. Cho DABC vuông cân tại A. D là trung điểm của cạnh AC. Từ A kẻ đường thẳng vuông góc với BD, cắt cạnh BC tại E. Chứng minh: AE = 2 DE
Gọi I là giao điềm của AE và BD. Lấy trung điểm của AE là K. Nối K với D.
Xét tam giác AEC: K là trung điểm của AE, D là trung điểm của AC => KD là đường trung bình của tam giác AEC.
=> KD//EC và KD=1/2EC (1) (Tính chất đường trung bình trong tam giác)
Do AE vuông góc với BD => Tam giác ABI vuông tại I. Mà tam giác BAD vuông tại A
=> Tam giác ABI đồng dạng với tam giác BAD. (g.g)
=> BI/AI = AB/AD=2 (Tính chất của 2 tam giác đồng dạng) => BI=2AI (2)
Song lại có: Tam giác AID vuông tại I => Tam giác AID đồng dạng với tam giác BAD.
=> ID/IA=AD/AB=1/2 => AI=2ID (3)
Từ (2) và (3) => BI=2AI=2.2.ID=4ID => BI=4ID => ID/IB=1/4
Do KD//EC (cmt) => KD/BE=DI/IB=1/4 => KD=1/4BE (4)
Từ (1) và (4) => KD=1/2EC=1/4BE => BE=2EC => EC/BE=1/2=DC/AB
Vì tam giác ABC vuông cân tại A => ^B=^C=450 => Tam giác ABE đồng dạng với tam giác DCE (c.g.c)
=> ^E1=^E2.(5)
KD//EC hay KD//BC => ^DKE=^E1 và ^KDE=^E2 (6)
Từ (5) và (6) => ^DKE=^KDE => Tam giác KED cân tại E
=> DE=KE. Mà K là trung điểm của AE => KE=1/2AE =>DE=1/2AE=> AE=2DE (đpcm)
cái bài này mình được anh trai mình chỉ , giải bài này theo cách lớp 8 , có gì cậu thông cảm nha . chúc cậu học tốt nha. nếu bạn muốn giải theo kiểu lớp 7 thì tìm link này nha:
https://olm.vn/hoi-dap/detail/248231624477.html
Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy hai điểm D,E sao cho BD=CE<BC/2. Đường thẳng kẻ từ D vuông góc với BC cắt AB ở M, đường thẳng kẻ từ E vuông góc với BC cắt AC ở N. Chứng minh rằng:
a) DM=EN
b) EM=DN
c) Chứng minh tam giác ADE cân.
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC ở D. Kẻ DE vuông góc với BC tại E.
a) Chứng minh DA = DE.
b) Chứng minh BD là trung trực của AE.
c) Kẻ CK vuông góc với BD tại K, các đường thẳng CK, BA cắt .nhau tại F. Chứng minh ba điểm E, D, F thẳng hàng.
d) Chứng minh BC - BA > DC - DA.
1. Cho tam giác ABC vuông tại A. tia phân giác góc B cắt AC tại D. từ A kẻ AE vuông góc BD tại E và cắt BC tại M
A. chứng minh tam giác ABC bằng tam giác MBE
B. chứng minh DM vuông góc với BC
C .Kẻ AH vuông góc với BC tại I. Chứng minh AM là tia phân giác của góc IAC
câu 2: Cho tam giác ABC cân tại A (góc A bé hơn 90 độ). vẽ tia phân giác AD của góc A (D thuộc BC)
A. chứng minh tam giác ABD bằng tam giác ACD
B. Vẽ đường trung tuyến của tam giác ABC cắt cạnh AC tại G. chứng minh G là trọng tâm của tam giác ABC
C. Gọi H là trung điểm của cạnh DC. qua h Vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh tam giác DEC cân
D. Chứng minh ba điểm B, G, E thẳng hàng
Câu 3 Cho tam giác ABC vuông tại A. Vẽ trung tuyến AM của tam giác ABC, Kẻ MH vuông góc với AC. Trên tia đối của tia MH đặt điểm K sao cho MK bằng MH
a. chứng minh tam giác MHC bằng tam giác MKB và BK vuông góc với KH
B. Chứng minh AB song song với HK và BK = AH.
C. Vẽ BH cắt AB tại g. Gọi I là trung điểm của AB. Chứng minh ba điểm C, G, I thẳng hàng
câu4 Cho tam giác ABC vuông tại A. gọi M là trung điểm cạnh BC. trên tia đối của tia MA lấy điểm D sao cho MD = MA.
A . chứng minh tam giác MCD bằng tam giác MBD và AC song song với BD
B. Gọi I là trung điểm AM, J là trung điểm BM. AJ cắt BI tại G. Chứng minh tam giác GAB là tam giác cân
Câu 5 cho tam giác ABC vuông tại A (AB bé hơn AC). vẽ BD là tia phân giác của góc ABC (D thuộc AC). trên đoạn BC lấy điểm E sao cho BE bằng BA
a chứng minh tam giác ABD bằng tam giác EBD .Từ đó suy ra góc BED là góc vuông
b. tia ED cắt tia BA tại EF. Chứng minh tam giác BED cân
C. Chứng minh tam giác AFC bằng tam giác ECF
D.Chứng minh: AB + AC >DE+BC
câu 6: Cho tam giác ABC vuông tại A. Vẽ đường phân phân giác BD của tam giác ABC và E là hình chiếu của D trên BC
a. chứng minh tam giác ABD bằng tam giác EBD và AE vuông góc với BD
B. Gọi giao điểm của hai đường thẳng ED và BA là F. Chứng minh tam giác ABC bằng tam giác AFC
C. Qua A vẽ đường thẳng vuông góc với BC cắt CF tại G. Chứng minh ba điểm B, D, G thẳng hàng
câu 7: Cho tam giác ABC cân tại A (góc A bé hơn 90 độ). vẽ AD là phân giác của góc A (D thuộc BC)
A . Chứng minh tam giác ABD bằng tam giác ACD
B. lấy H là trung điểm của AB. Trên tia đối của tia HC lấy điểm K sao cho HK = HC. Chứng minh rằng AK = BC
c. CH cắt AD tại G. Chứng minh (BA+BC)÷6 >GH
Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).